基于可变模糊集理论的生态脆弱地区水资源承载力时空变化研究

，

(华北水利水电大学 水利学院，河南郑州450046)

水资源是基础性的自然资源和战略性经济资源，是支持人类生存和可持续发展的重要资源[1]。除此之外，水资源还具有支持社会发展的潜力，具体而言，水资源不仅对于人口具有承载能力，还具有对经济发展的承载能力[2]。因此，有针对性地研究水资源承载力，对于区域可持续发展具有重要意义。尤其是对于干旱、半干旱地区，水资源紧缺已成为限制地区发展的重要因素，因此正确客观地评价水资源承载力已成为寻求区域可持续发展道路的重要依据[3-4]。

“承载力”一词源自于生态学，是用来衡量特定区域在某一环境条件下能够维持某一物种个体的最大数量[5]。随着水资源开发利用与社会可持续发展之间存在的矛盾日益突出，20世纪90年代以来，专家、学者们对于水资源承载力的概念提出了不同的理解：①在一定的生活标准和生态条件下，不影响社会和生态和谐的情况下，特定区域内可利用的水资源量可以支持城市规模、社会经济与生态环境协调发展的限度或能力[6]；②在某历史发展阶段下，基于可持续发展的原则，以社会经济发展水平为依据，以维护生态和谐发展为条件，经过科学地优化配置，能够提供给该区域经济和社会发展的最大支撑力[5]；③处于开发利用水资源的某个时期，满足生态用水的可利用总水量能够维系有限发展目标的最大的社会—经济规模[4]；④关于水资源承载能力定义的表述方式类似，即水资源承载力是基于社会、经济、人口、生态资源等复杂系统的耦合，衡量一个地区经济和社会发展受水资源制约的阈值[4]。

经过国内外学者多年的深入研究，水资源承载力的研究方法已从单一目标、静态分析发展到多目标、动态综合分析。施雅风[7]等运用常规趋势法，结合乌鲁木齐河流域实际情况，对其流域水资源承载力进行了评价，此方法是一种数学统计分析方法，通过选择单项或者多项指标，这些指标虽然可以直观、简便的反映区域水资源承载力的状况，但是此方法忽略了各指标间的关系，不能全面地反映研究区域的水资源承载力；陈冰[8]等将系统动力学法运用到柴达木流域水资源承载力评价中，此方法是一种复杂系统的计算机仿真模型。基于此方法的水资源承载力评价模型，分析速度快，但此方法结构复杂，变量多，对数据的要求高；翁文斌[9]等采用多目标分析法对华北地区水资源承载力进行了分析评价，多目标分析法通过降维算法，将研究问题转化为单目标进行规划，然后利用优化算法进行求解，确立目标函数和选择合适的降维算法是该方法的重点和难点。综合评价法通过建立评价指标体系，综合各指标值的评价结果，获得对水资源承载力更全面的判断。目前，综合评价的方法有很多，王顺久[10]等采用投影寻踪法对淮河流域水资源承载力进行了分析评价。上述综合评价法将水资源承载力评价标准或参照标准处理成点型，处理方法仍存在一定的不足。本文采用可变模糊集理论对玛纳斯河流域和塔里木河流域水资源承载力评价，能够科学、合理地确定样本指标对各级指标标准区间的相对隶属度和相对隶属函数，通过变化模型及其参数，可以合理确定出待评价样本水资源承载力的评价等级。

1 可变模糊模糊集理论

本文提出的区域水资源承载力评价的多指标、多级别的可变模糊集理论方法，基本原理如下[11-13]。

设区域水资源承载力有n个待评价的样本，样本集合如下：

x={x1,x2,…,xn}

(1)

用m个指标特征值来表示逐个样本的特性，待评价样本的特征值矩阵如下：

(2)

参考指标标准值矩阵和研究区域实际情况确定水资源承载力可变集合的吸引域矩阵：

Iab=([a,b]in)

(3)

其中，i=1，2，…，m(m为评价指标数)；h=1，2，…，c(c为级别数)。

根据已知Iab，可构造变动区间的范围域矩阵Icd：

Icd=([c,d]ih)

(4)

结合实际情况和标准区间矩阵Iab，确定水资源承载力的M矩阵：

M=(mih)

(5)

应用差异函数公式(6)—(9)，分别计算指标i对h级的相对隶属度矩阵：

当xi落在Mih左侧时：

(6)

(7)

当xi落在Mih右侧时：

(8)

(9)

h=1,2,…,c。

设m个指标的权重为：

w={w1,w2,…,wm}

(10)

根据式(11)计算样本j对各级别的综合相对隶属度：

(11)

式中wi——指标权重；m——指标特征参数；α——模型优化准则参数，α=1，最小一乘方准则，α=2，最小二乘方准则；P——距离参数，P=1，海明距离，P=2，欧式距离。

根据式(11)计算、归一化，得综合相对隶属度矩阵：

U= (μ(j) h)

(12)

级别特征值公式：

H=(1,2,…,c)·U

(13)

2 应用实例

2.1 玛纳斯河流域水资源承载力评价

2.1.1评价指标及分级

水资源承载力评价指标体系的制定基于研究区域的实际情况，均有差异，因此，没有统一的适用于全国范围的水资源承载力评价指标体系。不同地区水资源承载力评价的不同方案会有所偏重,如偏重经济,偏重生态,偏重社会效应等。衡量一个地区可持续发展的水资源承载力通常要综合考虑若干因素,使水资源承载的各项目标与区域可持续发展的目标保持一致。根据水资源承载力评价指标体系和本节研究区域的实际情况,并考虑到可操作性[6]，针对生态脆弱的内陆干旱区特点，选取具有科学性、代表性、系统性等特点的指标作为评价指标，见表1。该指标体系包括：水资源子系统、社会发展子系统、经济发展子系统、生态环境子系统4个方面，具有一定代表性。各分级标准及意义如下：I级为较优良，表示水资源的开发潜力较大，具有乐观的供给形势；III级为较差，表示水资源开发已趋于饱和，开发潜力小，如不采取相关政策、措施，将制约该地区的发展；II级则是介于I级、III级中间，表示该区域水资源的开发利用有一定规模，但仍有开发潜力，水资源量在一定程度上可以满足该区域的发展需求[14]。

2.1.2指标权重的确定

对于可变模糊集理论的水资源承载力评价模型，评价因子的重要程度由其指标权重反映，不同权重分配方案会得出不同结果；由于本文采用可变模糊集理论的水资源承载力评价模型得到的结果与升半Г型分布指数公式法[15]所得结果进行对比，升半Г型分布指数公式法采取的是等权重，为了使对比更客观，本文也采用等权重。

2.1.3确定综合隶属度

根据上文所述可变模糊集理论的水资源承载力评价模型，分别采用4种不同组合的模型参数，计算出级别特征值，评价结果见表2。

表1玛纳斯河流域水资源承载力评价指标分级标准及评价样本

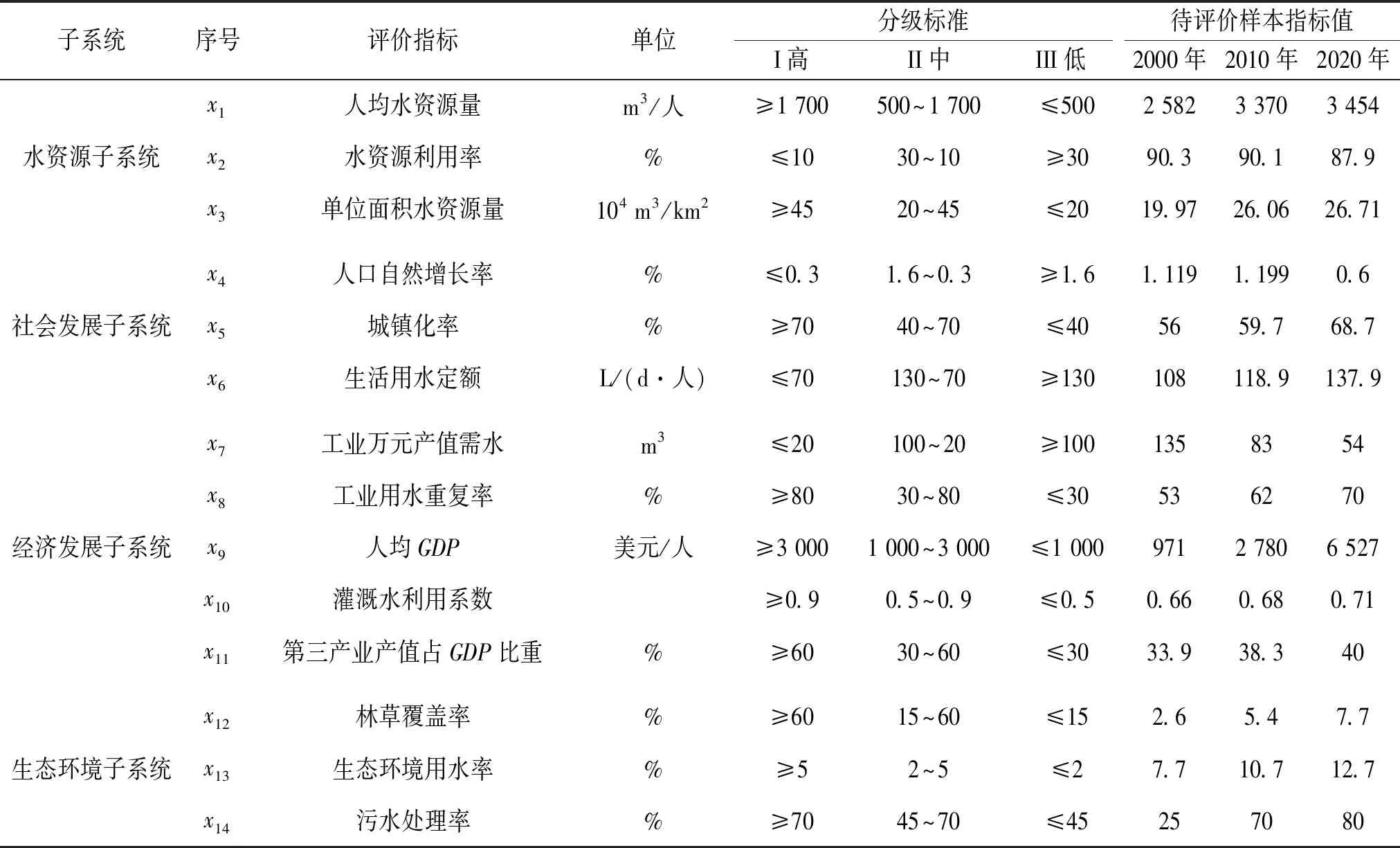
子系统序号评价指标单位分级标准I高II中III低待评价样本指标值2000年2010年2020年水资源子系统x1人均水资源量m3/人≥1 700500～1 700≤5002 5823 3703 454x2水资源利用率%≤1030～10≥3090.390.187.9x3单位面积水资源量104 m3/km2≥4520～45≤2019.9726.0626.71社会发展子系统x4人口自然增长率%≤0.31.6～0.3≥1.61.1191.1990.6x5城镇化率%≥7040～70≤405659.768.7x6生活用水定额L/(d·人)≤70130～70≥130108118.9137.9经济发展子系统x7工业万元产值需水m3≤20100～20≥1001358354x8工业用水重复率%≥8030～80≤30536270x9人均GDP美元/人≥3 0001 000～3 000≤1 0009712 7806 527x10灌溉水利用系数≥0.90.5～0.9≤0.50.660.680.71x11第三产业产值占GDP比重%≥6030～60≤3033.938.340生态环境子系统x12林草覆盖率%≥6015～60≤152.65.47.7x13生态环境用水率%≥52～5≤27.710.712.7x14污水处理率%≥7045～70≤45257080

表2 可变模糊集理论评价结果

2.1.4结果分析

4组不同参数组合的计算所得的4种组合级别特征值，求其均值后，直观地反映出不同参数组合下的评价结果稳定，证明了可变模糊评价法有着较高的可靠性。

表2中，2000、2010、2020年玛纳斯河流域的级别特征值分别为2.38、2.29、2.20，水资源承载力均处于II级，级别特征值随年限的增长逐渐减小，表明水资源承载力水平随年限的增长逐渐上升，与实际相符。

本文采用可变模糊集理论得到的水资源承载力等级和升半Г型分布指数公式法[15]结果在2000年和2010年一致，均为II级，但是在2020年略有差别，见表2。分析2020年玛纳斯河流域水资源承载能力，分析各指标实测值落入各级别的标准值区间，其中7个指标实测值落在II级区间，而4个指标值实测值落在III级区间，显然可变模糊集理论比升半Г型分布指数公式法[15]更加合理。

2.2 塔里木河流域水资源承载力评价

2.2.1评价指标及分级

塔里木河流域水资源承载力评价指标体系的选取原则如本文2.1.1所述，在此不再赘述。本节提出的塔里木河流域水资源承载力评价指标体系，包含7个指标，5个地区阿克苏、和田、克州、喀什、巴州地区，见表3。塔里木河流域概况见图1。

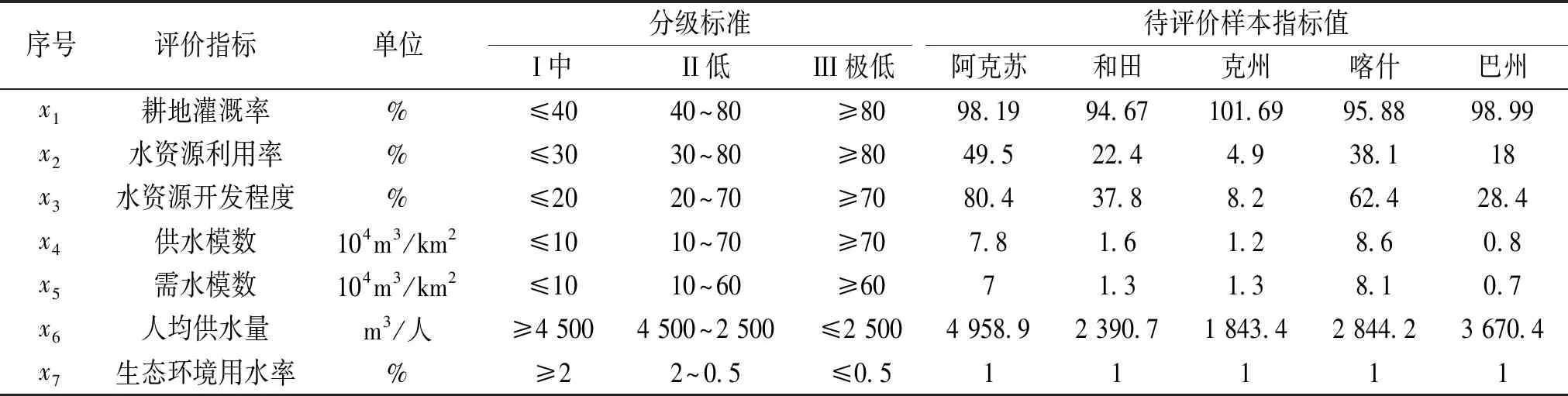
表3 塔里木河流域水资源承载力评价指标分级标准及评价样本

2.2.2指标权重的确定

对于可变模糊集理论的水资源承载力评价模

型，评价因子的重要程度由其指标权重反映，不同权重分配方案会得出不同结果；由于本文采用可变模糊集理论的水资源承载力评价模型得到的结果与升半Г型分布指数公式法[15]所得结果进行对比，升半Г型分布指数公式法采取的是等权重，为了使对比更客观，本文也采用等权重。

2.2.3确定综合隶属度

根据上文所述可变模糊集理论，分别采用4种不同组合的模型参数，计算出级别特征值，评价结果见表4。

表4 可变模糊集理论评价结果

2.2.4结果分析

由表3可见，塔里木河流域克州地区级别特征值为1.43，水资源承载力处于I级，阿克苏、和田、喀什、巴州级别特征值分别为2.05、1.60、1.95、1.57，水资源承载力处于II级，其水资源承载力从大到小依次为克州、巴州、和田、喀什、阿克苏。评价结果见图2，颜色越深表示水资源承载力越大。

本节采用可变模糊集理论得到的水资源承载力评价结果和采用的投影寻踪模型[16]得到的结果在地区水资源承载力排序上一致，与采用的升半Г型分布指数公式法[15]得到的结果在地区水资源承载力排序上大致相同，差别在于升半Г型分布指数公式法得到的水资源承载力评价结果是阿克苏>喀什；分析两地各指标实测值落入各个级别的标准值区间，耕地灌溉率、水资源利用率2个评价指标方面，阿克苏和喀什两地虽然一致，但是阿克苏实测指标值更大，水资源承载力更差；在水资源开发程度上，阿克苏为III级，喀什为II级，人均供水量阿克苏为II级，喀什为III级，且二文均采取的是等权重的情况，故可排除这2个评价指标的影响；综上所述，喀什水资源承载能力比阿克苏好。经过3种方法的对比可得，可变模糊集理论优于升半Г型分布指数公式法。

3 结论与展望

a) 本文基于可变模糊集理论对生态脆弱地区水资源承载力时空变化进行了研究，玛纳斯河流域水资源承载力水平逐年上升，塔里木河流域5个行政区水资源承载力水平存在差异；可变模糊集理论采用动态变化的标准值区间，能够准确计算出样本指标对于每一级指标标准区间的相对隶属函数、相对隶属度，同时改变评价模型及参数，最终确定出待评价样本的等级；通过与升半Г型分布指数公式法、投影寻踪法计算结果进行对比分析，结果表明，可变模糊集理论在水资源承载力评价中能够取得科学、合理的结果。

b) 结合本文来看，玛纳斯河、塔里木河流域2个研究区域评价指标体系及其标准存在差异，说明可变模糊集理论的关键在于建立科学、合理的评价指标体系及标准，评价指标能够有效反映研究区域水资源承载力的大小，目前评价指标的选择多是根据专家实践经验主观确定，对于评价指标体系的建立、评价标准的确定还有待深入。

c) 玛纳斯河、塔里木河流域水资源承载力等级近似均为II级，说明水资源开发潜力适中，为了实现水资源可持续利用的目标，结合评价指标体系，分析各评价因子隶属度，在研究区域未来的发展过程当中，应建立和实施合理的水资源开发、利用和保护措施。