一道中考压轴题的解法研究

王昌林 罗萍双 刘成龙

摘要：本文给出了2018年常州市中考物理第28题（Ⅲ）解答的三种视角和12种方法，

关键词：中考压轴题;视角;解法

研究试题解法是研究中考的基本形式和主要内容.对中考试题的解法研究一般可从一题多解、多题一解、错解分析等视角展开.其中，一题多解指的是对一道试题所涉及内容从横向和纵向进行把握，立足于不同的角度，运用不同的方法进行探讨，进而获得多种解法，下面对2018年常州中考第28题（Ⅲ）的解法进行深度剖析，以此加深读者对试题的深度认识！

试题如图1，二次函数y=-1/3x2+bx+2的图象与x轴交于点A、B，与）y轴交于点C，点A的坐标为（-4，0），点P是抛物线上一点（点P与点A、B、C不重合）.

（I）略;（Ⅱ）略;（Ⅲ）连接AC、BC，判断∠CAB和∠CBA的数量关系，并说明理由.

解（I）6=一5/6，点B的坐标为（3/2，0）;

（Ⅲ）的解答如下：

视角l 构造“半倍角模型”

思路1 由“倍角构造半角”，结合对称性解答.

解法l如图2，在x轴的正半轴上取A'，使BA'=BC，则∠CBA =2∠CA'B.

由题可得OB=3/2，OC =2，则BA'=BC=5/2，OA= OB+ BA'=4.故OA'=OA，从而有CA'=CA.

因此∠CAB=∠CA'B，即∠CBA =2∠CAB.

思路2 由“半角构造全角”，利用勾股定理与面积法求各边边长、求正切值.

解法2 如图3，取点C关于x轴的对称点C'，连接AC'，作CG⊥AC'于点G，可求tan∠CAG=CG/AG=4/3，且tan∠OBC=OC/OB=4/3

故∠CAG= ∠OBC，从而有∠CBA =2∠CAB.

思路3 由“半角构造全角”，利用勾股定理求正切值.

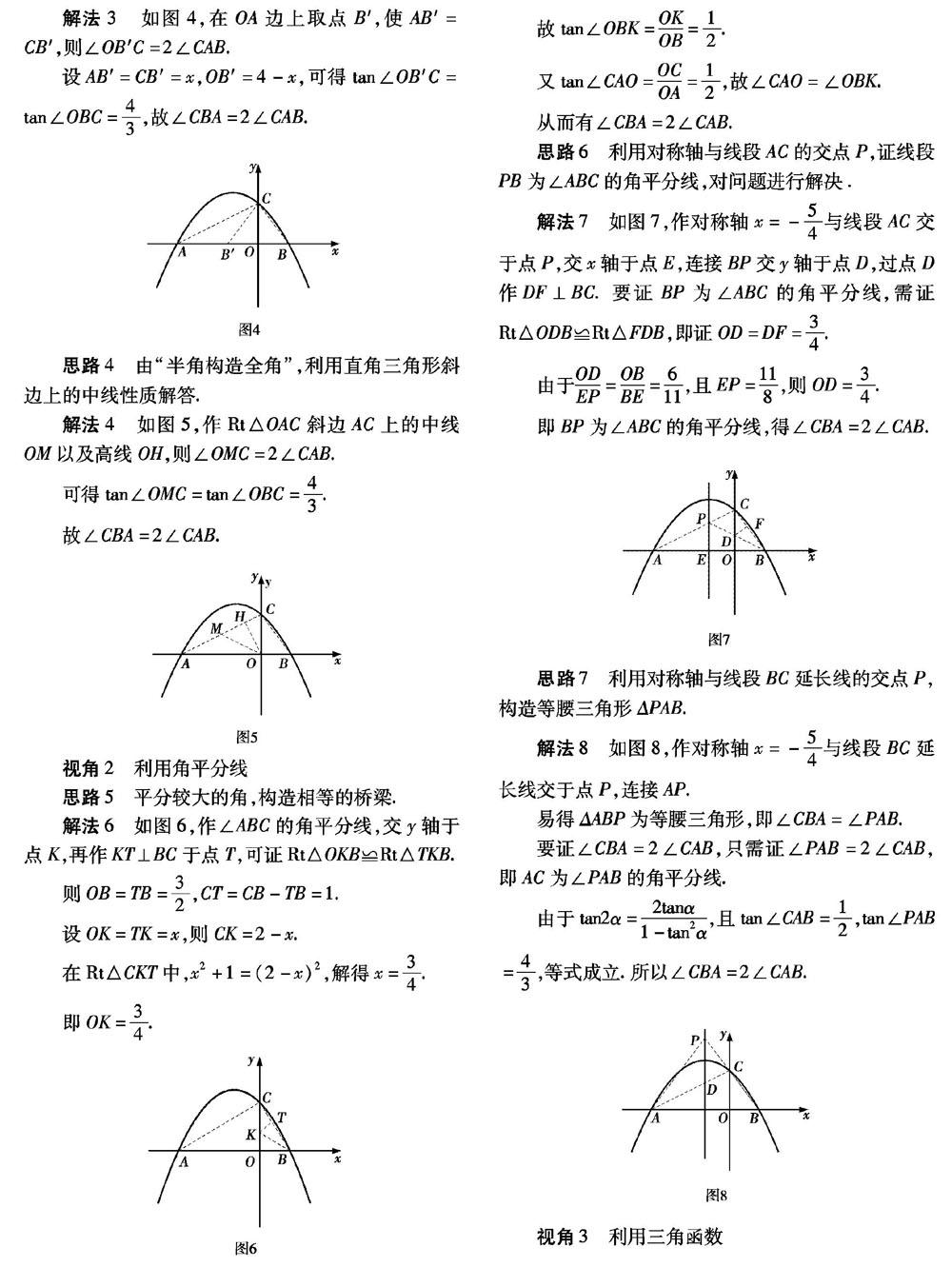
解法3 如图4，在OA边上取点B'，使AB'=CB'，则∠OB'C=2∠CAB.

设AB'=CB'=x，OB'=4 -x，可得tan ∠OB'C=tan ∠OBC=4/3，故∠CBA=2∠CAB.

思路4 由“半角構造全角”，利用直角三角形斜边上的中线性质解答.

解法4 如图5，作Rt△OAC斜边AC上的中线OM以及高线OH，则∠OMC =2∠CAB.

可得 tan∠OMC= tan∠ OBC=4/3.

故∠ CBA =2∠ CAB.

视角2 利用角平分线

思路5 平分较大的角，构造相等的桥梁，

解法6 如图6，作∠ABC的角平分线，交y轴于点K，再作KT⊥BC于点T，可证Rt△OKB≌Rt△TKB.

则OB=TB=3/2，CT=CB一TB=1.

设OK= TK=x，则CK =2 -x

在Rt△CKT中，x2+1=（2一x）2，解得x=3/4.

即OK=3/4.

文中给出的试题常规解法和高等（高中）解法，请读者细细品味解法间的关联性和独特性.