挖掘多维思考，注重数学解法

程丹

摘要：初中阶段的几何问题可以转化为代数问题，代数问题可以用几何形式呈现.一题多解的题目可以考查学生不同的能力水平与知识结构.本文以二次函数中有关不规则三角形的面积问题为例进行探讨.

关键词：抛物线;点的坐标;图形的面积

1 试题呈现

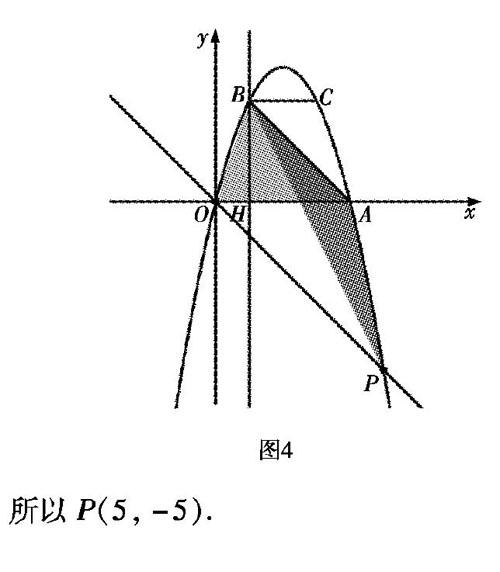
题目 如图l，抛物线y= ax2+bx过A（4，0），B（l，3）两点，点C、B关于抛物线的对称轴对称，过点B作直线BH⊥x轴，交x轴于点H.

（1）求抛物线的表达式;

（2）直接写出点C的坐标，并求出△ABC的面积;

（3）点P是抛物线上一动点，且位于第四象限，当△ABP的面积为6时，求出点P的坐标.

本题是以二次函数为背景的综合题.难度适中，入口宽，解法多，考查一次函数、二次函数、方程、整式乘法与因式分解、图形的面积等核心知识和消元轉化、数形结合、方程、模型、待定系数等数学思想方法[1].

（1）（2）问简单不再赘述，主要讨论（3）中不规则三角形面积.

2 妙解展示

解法1 割补法中的补全法

一道很普通的有关面积的二次函数题，挖掘其内在信息，包括一个数字，多角度思考，用常规思路去分析，发现不一样的风景，“6”竟然隐藏如此深的意义，数学的学习主要是思维的训练与培养，要学会不断从已知条件顺着常规方法去寻找最佳路径[2]，这也是数学的独特之美.

参考文献：

[1]谢盛强.以问题为抓手培养数学思考力——以《平行四边形面积》的教学为例[J].福建教育学院学报，2017，18（ 09）：51 - 52.

[2]许雯，对初中数学图形等面积拼接问题的教学反思[J].北京教育学院学报（自然科学版），2012，7（04）：54 -56 +68.