ADCP无效速度补偿算法研究
胡长和 王忠康
(第七一五研究所,杭州,310023)
1 引言
声学多普勒流速剖面仪(Acoustic Doppler Current Profiler,ADCP)通过Janus配置的四个波束向水中发射一固定频率的声波脉冲,传播过程中遇到水体中的散射体,发生散射。ADCP接收从声散射体返回的回波信号并对其进行处理得到不同深度单元层的径向流速,最后通过坐标变换获得绝对流速。这些声散射体是一些微小粒子、浮游生物及气泡等,它们随水体流动,所以发射的声波频率和接收到的声波频率会因为多普勒效应而产生差别,ADCP通过信号处理得到这一频率差值,计算出与散射体之间相对运动的速度[1]。
对实际海试数据分析发现,ADCP工作存在以下两个问题:
(1)实际测量环境中很难保证水体中散射体是均匀分布的,因而会造成某个波束的海底或某部分深度单元层的回波信号强度过低而被噪声淹没,此时所测得的对应径向流速无效(回波信号信噪比过低)。
(2)海深较深时,ADCP斜向下发射四个波束照射范围较大,无法保证所有波束都在测量同一个流速矢量,即无法保证四个波束所在流场均匀,此时再进行速度合成所得到的结果是不合理的,如图1所示[2]。

图1 平面速度不一致性误差
上述问题导致最终得到的速度合成结果质量差。因此,如何对有问题的数据进行有效补偿、重新计算是我们亟待解决的难题。原始方法直接剔除问题数据,采用平滑的方式进行替代,导致数据利用率低。为此,本文提出一种ADCP无效速度补偿算法,用于改善整体数据质量,提高数据的利用率。
2 流速数据补偿标准的确立
2.1 波束径向流速无效判据
测速精度与回波信号信噪比相关,当信噪比过低时,回波信号被噪声淹没,此时所测得的对应径向流速无效,回波信号信噪比在实际中直接计算不方便,本文引入相关系数的概念。相关系数可以反映测量过程中最近一段时间内的回波信噪比,由复相关算法可得到参与复相关运算的回波信号的互相关函数值,与自相关函数值的比值作为波束在该深度单元的相关系数值。
以300 kHz ADCP为例,设定4阶M序列[1001],共15个码元,每个码元填充10个周期的正弦信号,填充信号频率300 kHz。四倍采样,信号采样频率为4×300 kHz。每个码元填充信号的起始相位由M序列决定。设定信号多普勒频移为50 Hz,信噪比取–30~30 dB范围,步进1 dB,每个信噪比做1 000次蒙特卡洛仿真,用复相关算法得出多普勒频移fd,取相对误差均值、相关系数均值。统计图见图2。由图可以看出,300 kHz声学海流剖面仪在–13 dB信噪比时相对误差为1%左右,此时对应的相关系数为78.03。
选取2019年10月300 kHz声学海流剖面仪的试验数据进行验证。图3为300 kHz ADCP四个波束测量的原始波束速度和对应的相关系数随剖面深度距离变化曲线。在速度测量值图中,分别选取数据质量较好的最大测量剖面距离标注,并标注出其对应的相关系数。选取出一个相关系数80,保证大于该值的相关系数所对应的剖面距离的速度测量数据质量较高。
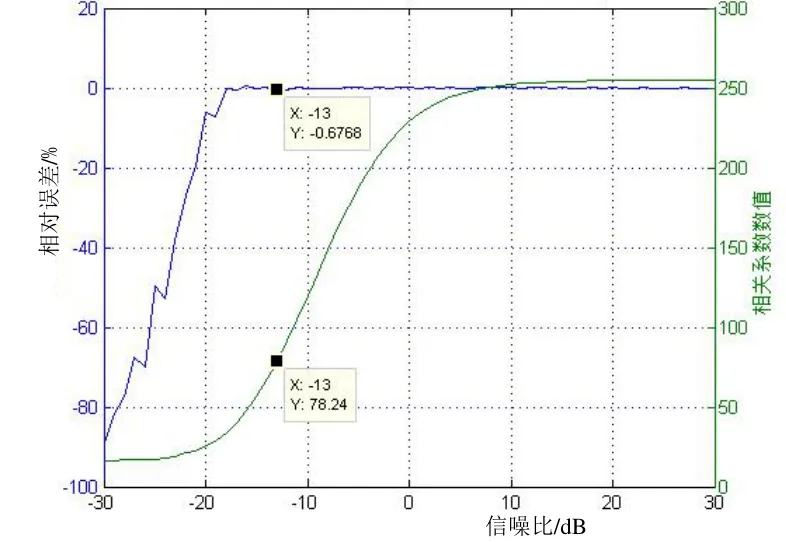
图2 相关系数统计图
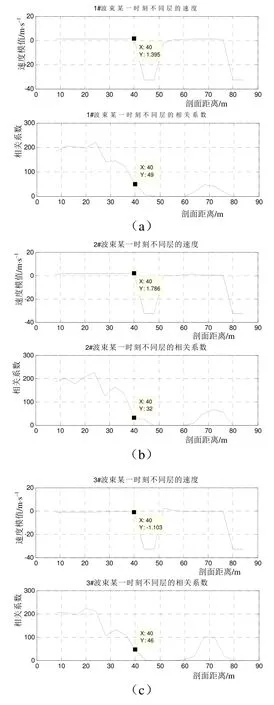

图3 4波束速度和相关系数随剖面距离变化曲线
为了进一步验证该系数的正确性,对大量 300 kHz ADCP测量对地速度数据,按上文所得的相关系数门限值80进行野值剔除,并与GPS速度进行比对,如图4。对大量300 kHz ADCP测量对水剖面速度数据,按上文所得的相关系数门限经验值进行野值剔除,并与原始速度进行比对,如图5。从图4中可以看出,按照相关系数门限对数据进行处理后,对地速度数据中偏离GPS测量值较大的野值点基本被剔除。
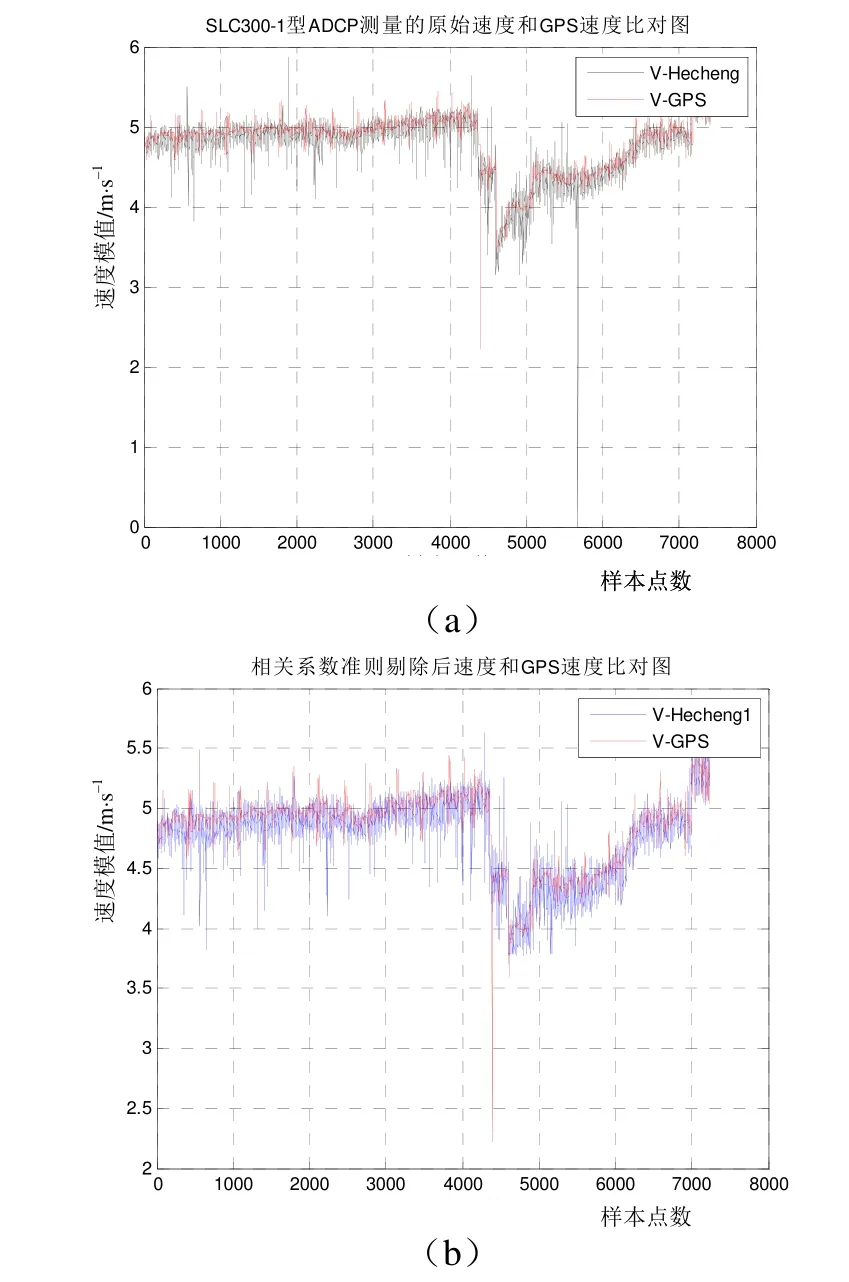
图4 GPS-300kHzADCP速度比对图
从图5中可以看出,对水剖面速度数据中质量较差的数据也被剔除。测量速度曲线更加接近测量的真实值,极大地提高了测量的精度。当数据因信噪比过低、相关系数未达到门限值判为无效时,设定其输出结果为一定值(本文选为–32.768)。
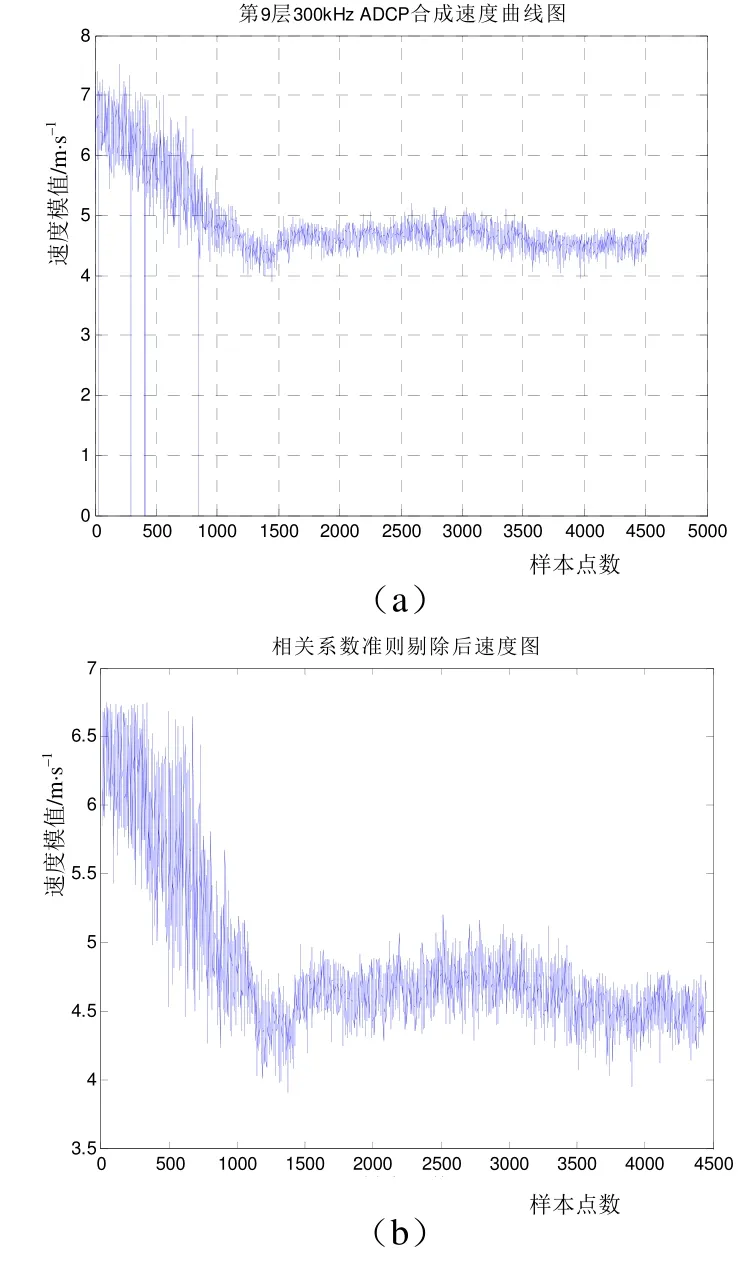
图5 300 kHz ADCP剖面速度比对图
2.2 补偿标准-质控因子
V0、V1、V2、V3分别为四个波束径向速度,船载ADCP对称波束结构,因此对于两两对称波束的正常径向速度数据应有V0+V2=0、V1+V3=0。定义Verror为反应波束径向流速质量的计算因子,Verror=V0+V1+V2+V3或Verror=V0–V1+V2–V3,正常时数值应接近0,本文选后者为质控因子公式。
当某一个波束径向速度数据无效时,设定其输出结果为一定值。因此当某一个或多个波束径向流速出现无效数据时,质控因子会很大。本文将质控因子作为确立流速数据是否需要补偿的标准(质控因子越大,波束径向流速质量越差)。
3 三波束方法依据
ADCP工作时斜向发射四个波束,图6是四个波束在水平、垂直面的位置投影分布图。由波束几何位置图推出:

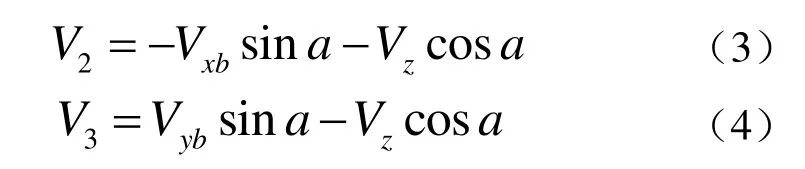
若四波束径向速度质量好,联立式(1)~(4)可以解得:
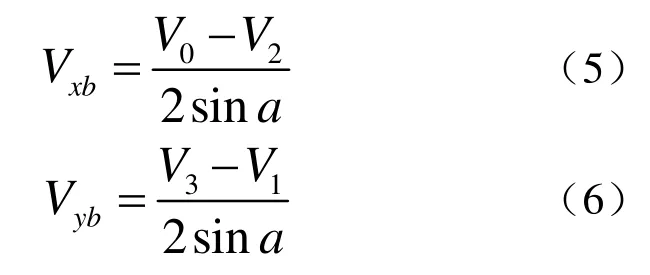
若4#波束径向速度质量差,联立式(1)~(3)可以解得:

同理可得,若 3#、2#或 1#波束径向速度质量差,联立其它三个方程同样可得Vxb、Vyb。

图6 波束几何位置投影图
通过公式推导,可以发现,ADCP测量中三个空间上相互独立的波束信息就可获得完备的流速,冗余波束信息则为流速提供校验。因而,当某一个波束信息完全失效时,可以利用其余波束数据进行进行补偿[4]。
4 三波束新方法流程
(1)选择处理数据起始点(例如第4批数据),设置第一批起始合成速度值,以质控因子为标准,选取起始点之后的一批有效数据合成速度值作为起始合成速度,代替原始起始点合成速度值;
(2)输入值为起始点之后(例如第5批数据)的四个波束计算出的波束径向速度值(V0、V1、V2、V3);
(3)以质控因子为标准,计算每批数据质控因子数值,确定需要重新处理的数据(质控因子绝对值大于1);
(4)由第 3步分辨出波束径向流速差的数据进入下一步流程,其余数据按照四波束合成方法合成速度数值,流程见图7。
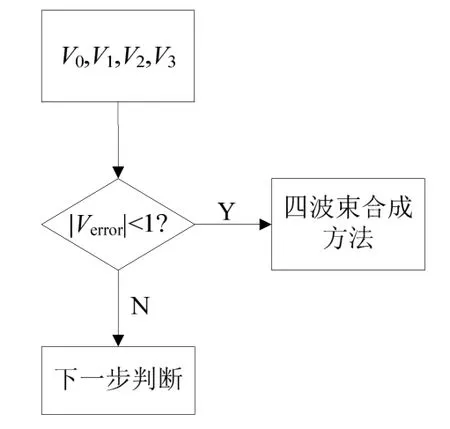
图7 第4步流程图
(5)四个波束速度值是否出现–32.768(无效波束),若有则判断无效波束的个数及编号,否则进行下一步流程。若无效波束个数超过1个,采用前一批合成速度值代替本批次合成速度值,反之,采用3节三波束计算方法进行计算。流程见图8。
(6)V为前一批数据合成速度值(速度随时间是慢变化的,选择前一批数据合成速度值作为参考),定义变量

设定判决门限值为0.1(0.1为多批数据实际分析选择得到)。结果分为以下几种情况:
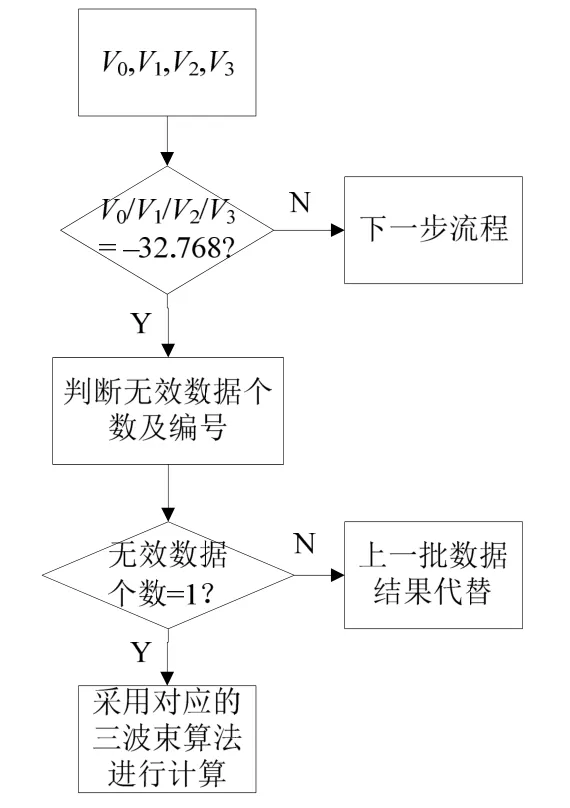
图8 第5步流程图
5 实验结果分析与验证
5.1 仿真验证
设定V0为1 000批取值1~2的随机数,V1为1 000 批取值 2~3的随机数,V2= –V0,V3= –V1。改动V2第400批数据数值为–32.768(对应前面所述第一个问题),改动V3第800批数据数值为0.8(对应前面所述第二个问题)。使用 Matlab 软件对本文提出的数据补偿方法进行测试。从图9中可以看出本文提出的方法可以很好的解决前面所述的两个问题,成功的补偿了第400批和第800批异常数据。


图9 结果对比图
5.2 实际数据验证
数据来自于第七一五研究所自主研发的 Janus配置300 kHz ADCP在南海某海域测量的,10月采集,海况3级,海深约50 m。从测得的ADCP数据挑选出含有无效值的一段数据,采用本文算法与原有算法分别进行处理,最后对处理结果进行比较,见图10。GPS速度是通过高精度船载GPS设备计算所得载体相对于大地的速度;底跟踪速度是通过ADCP设备计算所得载体相对于大地的速度。GPS速度作为评价的参考。


图10 底跟踪结果对比图
图10(a)、(b)对比可以看出,改进前算法存在质量差的数据;图10(a)、(c)对比可以看出,改进后算法可以有效的补偿质量差的数据,获得更为平稳的结果数据,整体数据分布与GPS速度分布相同,用本文方法处理的速度结果成功地补偿了异常数据。
6 结论
本文所提出的质控因子和三波束新方法能够在已有的有效数据基础上提高数据的利用率,补偿和改善数据质量。在仿真结果中,得到了较好的处理结果。仿真结果中仍有部分结果数据质量较差,分析原因是四个波束径向数据中质量差的个数超过一个,且持续时间很长,导致三波束方法无法准确补偿,无法提高这段数据的利用率,仍需进一步的研究。

