弯张换能器密排成阵性能的研究
顾汉炳 夏铁坚 郝浩琦
(第七一五研究所,杭州,310023)
随着西方国家潜艇浮筏减振、复合消声瓦技术的发展,潜艇自噪声进一步降低,隐蔽性增强,中高频主动声呐对敷瓦潜艇的探测距离大幅下降,低频大功率主动声呐目前在世界上被认为是对敷瓦潜艇最有效的探测手段[1]。
在0.3~3 kHz频段内的大功率发射换能器中,弯张换能器综合性能最优,其流线型的外型结构、较小的体积重量、极高的功率/体积比等特性,尤其适合充当低频主动拖曳系统的声源[2]。为获得更高的声源级和特定的波束宽度,一般采用多个弯张换能器组合布阵。而换能器成阵最为关注的是如何在有限的空间内实现声源级、带宽、指向性等指标的最优设计。基于上述需求,本文对弯张换能器不同间距、不同布阵形式下性能进行了研究。
1 单换能器性能
IV型弯张换能器由一椭圆柱壳体和内部的驱动振子组成,通过驱动振子的伸缩运动来带动壳体的弯曲振动。由于椭圆壳体具有位移放大的效果,使得长轴方向较小的伸缩振动在短轴处被放大,从而实现小尺寸低频大功率声辐射。
IV型弯张换能器结构较为复杂,利用常规的理论计算难度较大且精度较低,因此通常采用有限元方法来进行仿真分析。图1是一个常规IV型弯张换能器有限元模型。对该换能器进行空气中的模态分析,提取其一阶振动位移矢量图如图2所示。从图中可以明显地看出短轴处的振动位移远大于长轴,并且长短轴上振动位移相位相反,因此长轴端的振动位移对总响应起了削弱的作用。
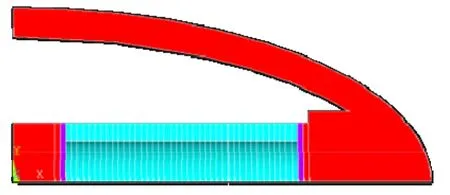
图1 单换能器模型图
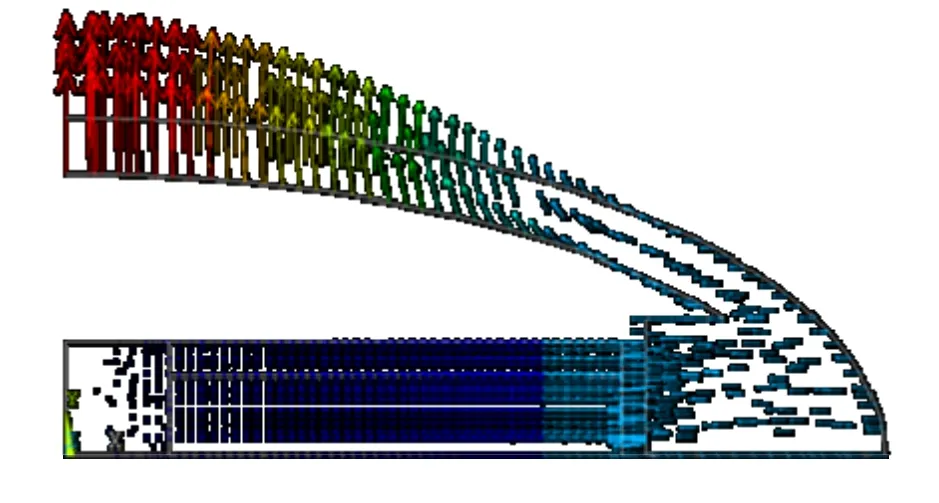
图2 单换能器谐振点振动位移图
建立水中模型并进行谐响应分析,获得换能器各方向发送电压响应如图3所示(图中横坐标以谐振频率f0对频率进行归一化处理,下文同)。
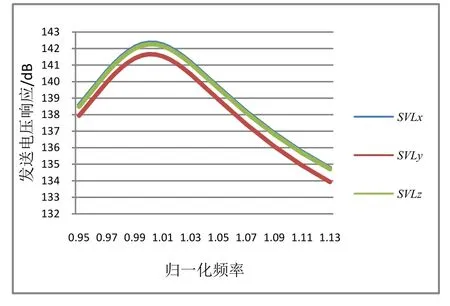
图3 单换能器水中发送电压响应
图3中SVLx指的是长轴方向的发送电压响应,SVLy指的是短轴方向的响应,SVLz指的是高度方向的响应。从图3中可以看到长轴方向的响应最大,短轴方向的响应最小,高度方向与短轴方向接近,但比短轴小,这可以通过四极子模型来进行解释(见图4)。
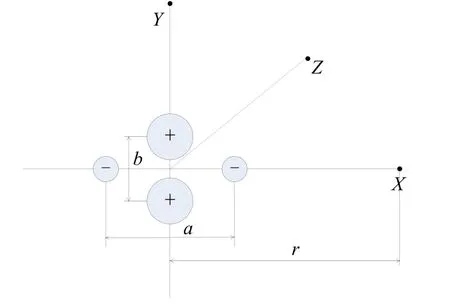
图4 单换能器四极子模型
四极子模型主要是将整个换能器等效为四个小脉动球源。短轴部分两侧壳体为主要振动位置,振动位移大,因此等效为振幅较大的正极子部分;长轴部分反向振动,且振动位移相比正向振动部分小很多,因此理解为体积较小的负极子。b表示两正极子部分的等效间隔,a表示两负极子部分的等效间隔,由换能器长轴大于短轴的结构可知a>b。X、Y、Z分别表示长轴、短轴和高度方向远场观察点,到换能器中心的距离都为r。则求空间辐射的声压只要将这四个脉动球源在空间上的声压叠加即可[3]。
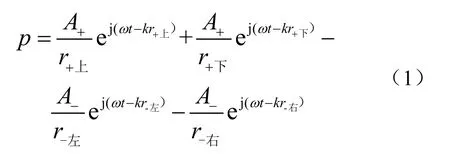
式中,r+上和r+下分别表示两个正极子到观察点的距离,r-左和r-右分别表示两个负极子到观察点的距离。表示正负极子的声压振幅,kr+上、kr+下、kr-左和kr-右分别为不同极子点到观察点的相位。由于仅考虑离声源较远处的声场,小球源辐射的声波到达观察点的振幅差别较小,因此可以将上式中振幅部分的r+上、r+下、r-左及r-右都近似用r来代替,但相位差异不可以忽略。因此换能器远场观测点的响应值大小主要受两个因素的影响,一是换能器极子点的振幅二是不同极子点到远场观测点的相位差kr差。对于幅值而言,由于远场声压变化主要受等效正极子部分影响。对于相位差而言,由于换能器尺寸原因,声程差r差≤ 半波长,即相位差在0°~180°的变化中,相位差越小,表示越接近同向叠加,响应更大。
运用此模型对单换能器各方向的响应规律进行解释:两个正极子到长轴方向观察点X和高度方向Z的声程相同,响应同向叠加,而到短轴方向观察点Y时即存在相位差,非同向叠加,削弱响应大小,因此短轴方向的响应比长度和高度方向要小。而长轴方向由于两个负极子到达观察点X存在声程差a,使得长轴方向负极子点对总响应产生的削弱作用降低,因此稍比高度方向响应高。
2 二元不同布阵形式
经典的布阵方式通常采用1/2波长布阵,导致占用空间较大。因此考虑密排布阵的形式,一方面压缩整体阵体积,另一方面利用互辐射获得宽带、降低频率等的效果。为了便于模型的简单化,对最基本的二元阵进行分析。二元阵布阵通常采用三种形式:长轴排列、短轴排列和高度方向排列。
2.1 长轴方向密排成阵
图5是换能器长轴排列的布阵形式。长轴方向本身尺寸较长,考虑布阵间隔从1/2波长缩减至1/4波长,以1/8波长为间隔(布阵间隔指的是换能器中心点之间的间隔)。具体仿真结果如表1所示(表中以单换能器谐振频率f0对频率和带宽进行归一化处理,下文同)。

图5 长轴密排形式
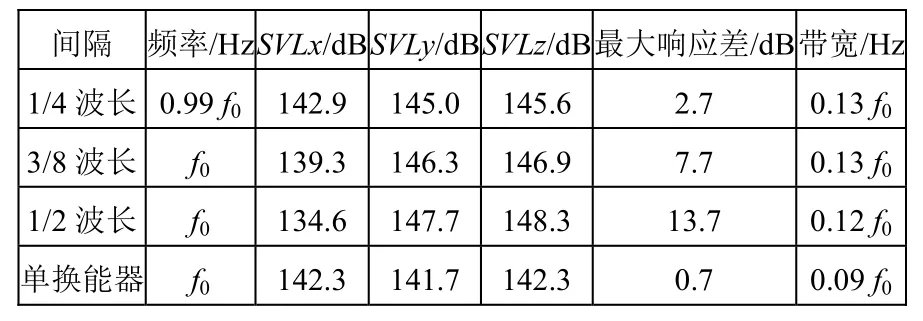
表1 长轴密排仿真结果
为便于对比,表中加入了单换能器的一些数据。从表1中可以看出随着布阵间隔的减小,谐振频率变化幅度不大,响应差别较大,带宽有了一定程度上的增加。
2.1.1 不同间隔下谐振点响应值分析
整理不同布阵间隔下各方向的谐振点响应值如图6所示。从同一间隔下谐振点的响应可以看出,当换能器按长轴方向排列之后,高度方向的响应最大,短轴方向的响应次之,长轴方向的响应遭到了较大削弱,短轴和高度方向的响应较为接近。这也可以通过四极子模型来进行解释。
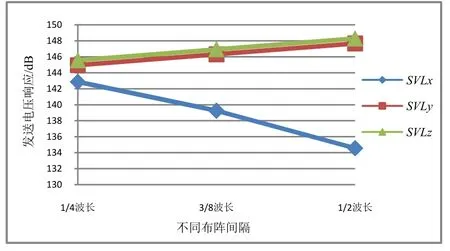
图6 谐振点不同间隔不同方向响应曲线
由之前单换能器四极子模型可知,响应受幅值和相位的影响。因此从这两个角度来进行分析。在同一个布阵间隔下,换能器振动位移一致,幅值相同,主要受相位影响。图7中,左侧正极子点和右侧正极子点到长轴观察点X的声程差为布阵间距L,到短轴观察点Y的声程差为b,b<L。因此长轴方向相位差更大,这就使得长轴端极子的声压叠加更小,长轴方向的发送电压响应值比短轴方向更低。而高度方向由于仍是同向叠加,响应是最大的。
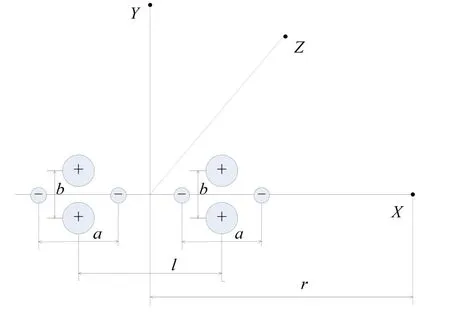
图7 二元阵长轴排列四极子模型
从同一方向不同布阵间隔下的谐振点响应可以看出,短轴和高度方向的响应值随布阵间隔的减小而下降,长轴方向的响应值随布阵间隔的减小而上升。图8为密排之后换能器谐振点长短轴方向的振动位移,从图中可见,主振部位短轴轴点位置的振动位移随着布阵间隔的减小而下降。这主要是由于当布阵间隔减小之后,相互脉动球源之间的互辐射作用逐渐加强,抑制了壳体的振动位移。这就造成了极子点声压幅值大小的下降。高度方向和短轴方向随着布阵间隔的变化,极子点到观测点相位并没有发生变化,响应主要受幅值影响,因此随布阵间隔的下降,响应有了一定程度上的削弱。但长轴方向与高度、短轴方向不同,极子点到观测点的相位随布阵间隔的减小而下降,逐渐向响应同向叠加转变,此时相位差对响应产生的影响远比幅值大,因此长轴方向谐振点的响应反而随着布阵间隔的下降而上升。
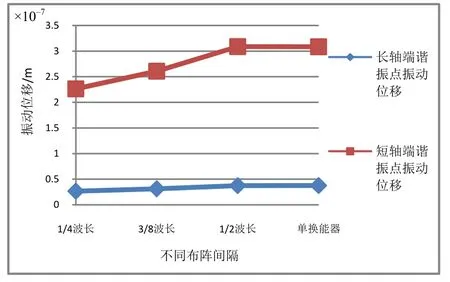
图8 谐振点不同间隔不同位置振动位移
2.1.2 不同间隔下谐振点指向性情况分析
由于上下盖板通常安装在高度方向上,并从盖板方向进行吊放测试,因此指向性情况主要考虑的是换能器长短轴所在平面。读取不同布阵间隔下换能器谐振点的水平面内指向性(即长短轴平面),如图9所示(0°表示长轴方向,270°表示短轴方向,下文同)。
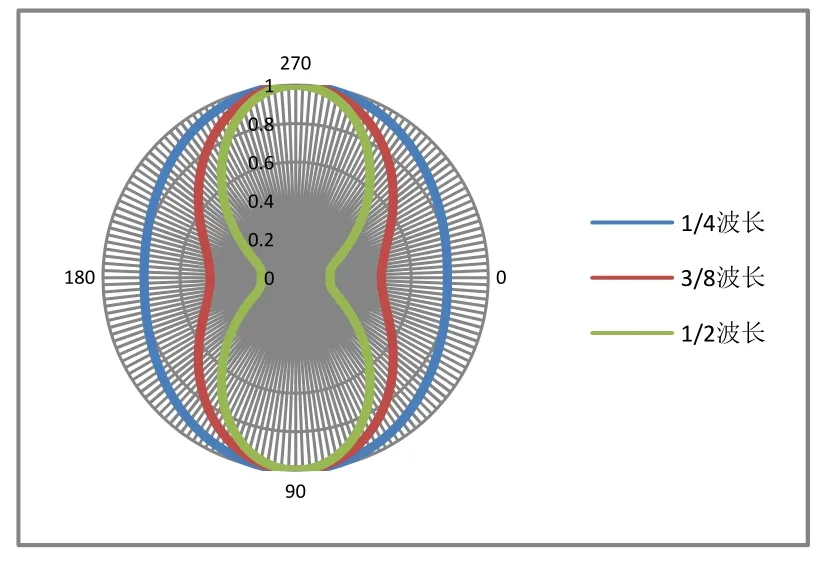
图9 不同间隔下谐振点指向性
当1/2波长布阵时,由四极子模型的分析可知两侧正极子到长轴观测点X的相位相反,响应反向叠加,削弱最为严重,形成“8”字指向性。随着间隔的不断减小,相位差不断减小,各方向响应值逐渐接近,最大响应差由之前的13.7 dB逐渐缩减为2.7 dB,即由“8”字指向性往全指向性发展。
2.1.3 不同间隔密排下宽带响应分析
由表1已经可以看出,当换能器的布阵间隔减小后带宽有所增加。这主要是由于谐振点互辐射作用强,响应值削弱较大,而远离谐振点互辐射作用较小,响应值削弱较少所引起的。但是该带宽主要表示谐振点附近的响应曲线变化,允许波动范围较小,缺少整个工作频段内响应情况。给出二元阵在0~3.3f0Hz以内的响应曲线,见图10~12。从图中对比可以看出,高度和短轴方向的响应曲线变化幅度不大,主要是对谐振点附近的响应值产生影响。原因是随着布阵间隔的减小,互辐射作用逐渐增强,削弱了谐振点的响应值,使得谐振点附近带宽增加。这点在表1的带宽中也可以看出。

图10 1/2波长布阵响应曲线
图11 3/8波长布阵响应曲线
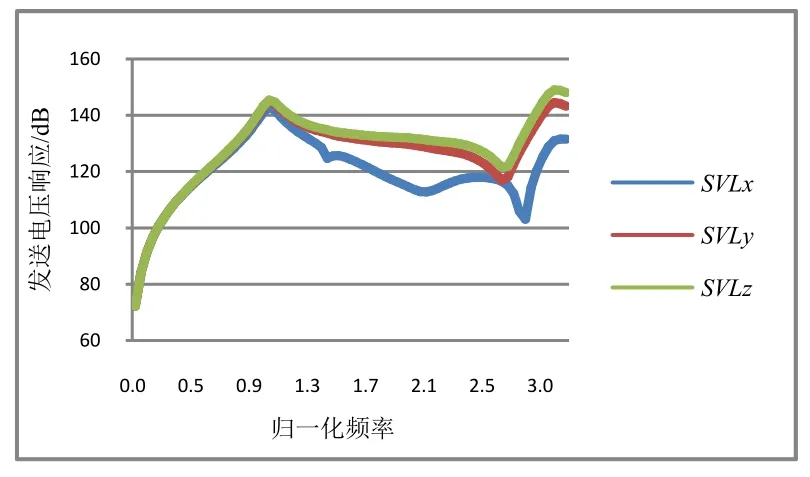
图12 1/4波长布阵响应曲线
而长轴方向的响应曲线受换能器密排布阵的影响较大,存在一个明显削弱的凹谷,随着布阵间隔的减小,这个凹谷逐渐从一阶谐振位置向二阶移动。分析其原因,也可以用四极子模型来解释。在凹谷位置时,换能器极子点到长轴方向观察点的声程差为1/2波长,左侧极子点和右侧极子点相位差近似180°,声压反向叠加,使得响应值较低。声压反向叠加位置的条件为:

当布阵间隔减小时,声程差r差减小,声压反向叠加位置的频率增大,因此响应凹谷位置逐渐向高频移动。举个例子来说,当间隔为1/4波长时,换能器间隔为:

将其代入声压反向叠加位置的条件,可得:

解得f=2f0,即当频率在2f0左右时,左右两侧极子点到长轴观测点的相位差满足180°,响应反向叠加削弱,从图12中看到当1/4波长为间隔时确实在2f0左右存在一个较深的凹谷,理论与实际相符合。
在这个凹谷位置,响应差值会达到近15 dB,出现较为明显的指向性,这对宽带较为不利,因此在密排布阵时需要通过调节间距将此凹谷移到所需工作频段之外。
2.2 高度方向密排布阵
图13是换能器高度排列的布阵形式。不同高度间隔下换能器阵的性能如表2所示。高度方向比长轴方向排得更密,因此加入了在超小间隔10 mm下的换能器性能(10 mm指的是两换能器高度方向中间水域的间隔)。为了增加对比性加入了单换能器的性能。

图13 高度密排形式
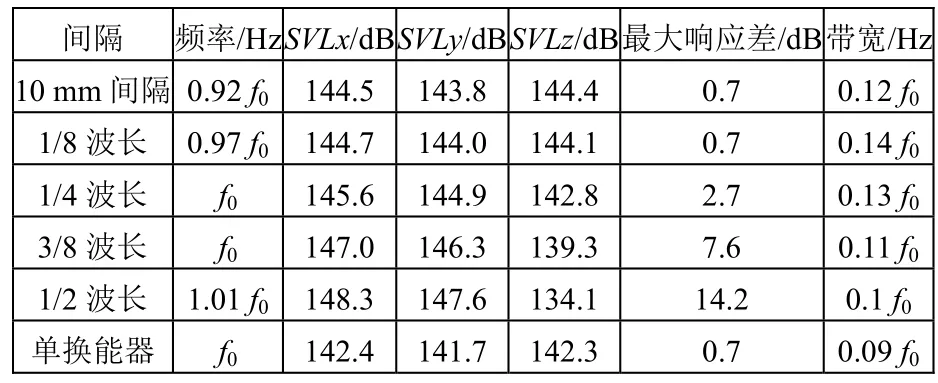
表2 高度方向密排仿真结果
基本规律同长轴排列的四极子模型解释类似,需要注意的是,高度方向密排主要影响的是高度方向的响应。当间隔<1/8波长时,对响应层面上的削弱较小,各方向响应大小规律基本和单换能器一致,主要影响换能器谐振频率。同时极小间隔10 mm布阵时,带宽不再随布阵间距的下降而上升,反而呈现下降趋势。以下针对这两个不同点进行解释。
(1)小间隔下谐振频率的下降
换能器谐振频率的计算公式为[4]:

式中,keff是换能器的等效刚度,meff是换能器的等效质量。在小间隔排布下,换能器之间的互辐射作用增强,使得互辐射抗增加,从而弯张换能器的同振质量增加,增大了meff,因此较大程度上降低其谐振频率。
(2)极小间隔下带宽的下降
文献[5]中两个脉动小球源之间的互辐射作用见图14。从图中可以看到,在极小间隔下,互辐射抗的作用急剧增加,但互辐射阻增长不大,趋于稳态;而在1/2波长~1/8波长区间,互辐射阻值远比抗值的增加大。
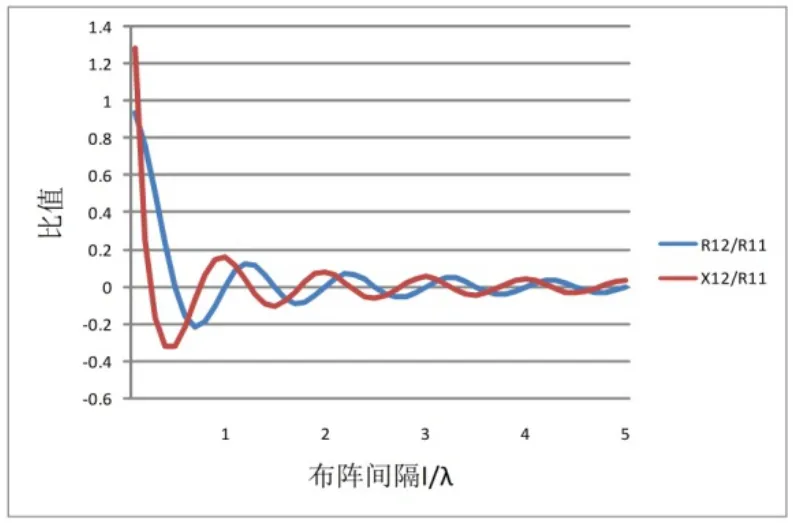
图14 互辐射阻与抗随间隔变化示意图
对于单一振动模态单一谐振的换能器,其带宽特性的定义是用机械品质因数Qm值来表示:

式中,fr表示的是单一谐振频率,Δf是电导响应下降3 dB的频带宽度。用等效集总参数类比电路可将Qm值写成:
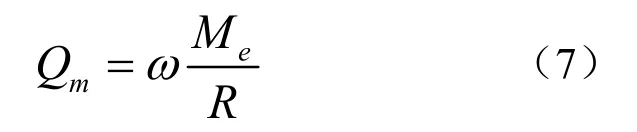
式中,ω为谐振角频率,R为换能器的辐射阻、机械损耗阻之和,Me是换能器的等效质量。
由脉动小球源间互辐射理论得到,在极小间隔下,互辐射抗急剧增加,而互辐射阻增加较少,即等效质量的增加远大于等效阻值,因此品质因数Qm增加。而fr由于互辐射抗的增加有一定程度的下降,因此由式(6)可知,Δf必定有所下降。
利用该理论也可以从另一个角度解释为何布阵间隔从1/2减到1/8时,带宽反而有所增加。在这个阶段互辐射阻的增加远大于互辐射抗,这就使得R增加,导致Qm值下降,在谐振频率fr变化不大的情况下,由式(5)可得Δf有所上升。总的来说,这几个参数之间是互相产生影响的,在1/8波长为间隔时带宽最大。
2.3 短轴方向密排布阵
图15是换能器短轴排列的布阵形式。短轴方向不同间隔下阵的性能如表3所示。基本规律同长轴排列,短轴密排主要影响的是短轴方向的响应。小间隔下也降低了谐振频率,增大了带宽。

图15 短轴密排形式

表3 短轴方向密排仿真结果
3 实际测试
仿真过程中为了简化运算,仅针对两元阵进行分析。当多元密排时就相当于将二元密排中的规律进一步强化。本文利用现有的换能器进行测量,选择了几组实测数据与仿真规律进行对比。
3.1 高度方向多元密排降低频率
以5 mm为间隔从高度方向不断增加换能器数量,响应如图16所示,图17是与之对应的仿真结果图。从图16~17可见,当高度方向密排的换能器数量增加之后,谐振频率下降。仿真结果与实际较为符合。
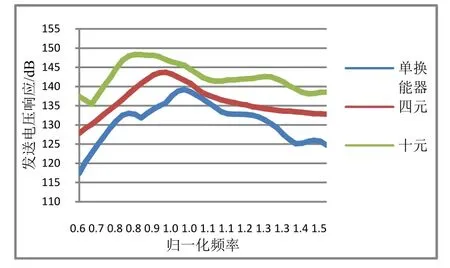
图16 多元阵最大响应方向发送电压响应实测值
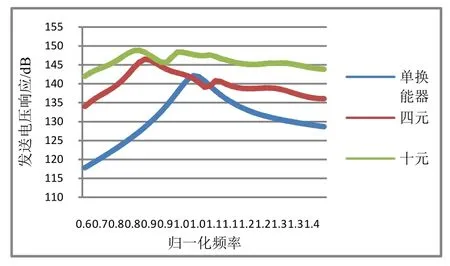
图17 多元阵最大响应方向发送电压响应仿真值
3.2 密排增加带宽
两列四元阵短轴方向1/4波长密排,单列激发和两列同时激发下的响应如图18,对应的仿真结果见图19。由图中可以看出,谐振点附近受互辐射影响,削弱响应,并且增加其带宽。实测结果与仿真一致。
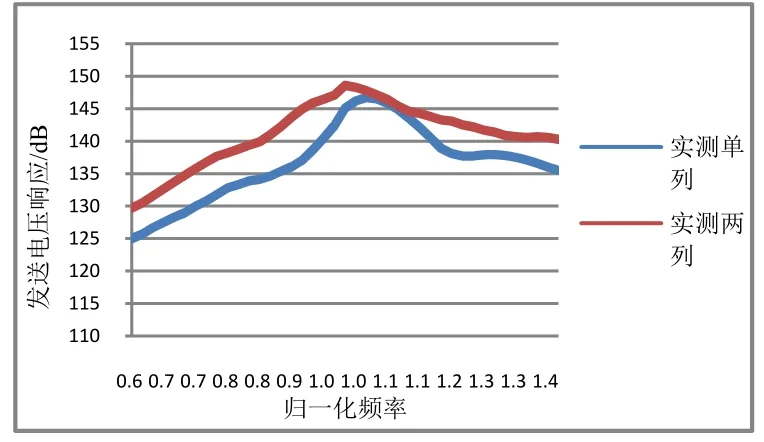
图18 单列与两列阵发送电压响应实测值
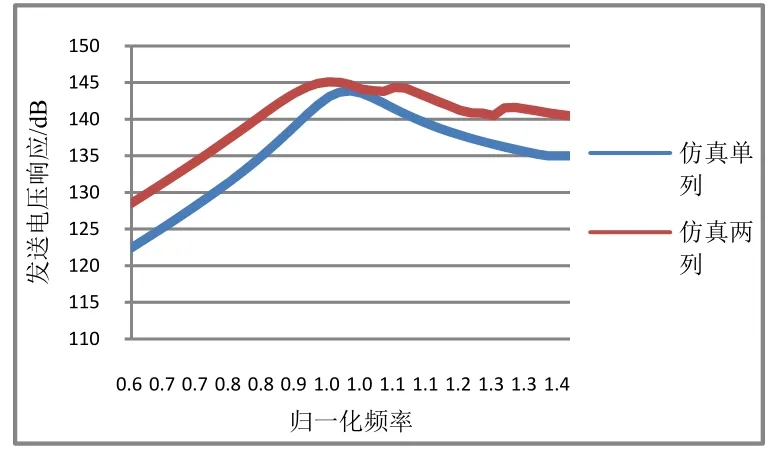
图19 单列与两列阵发送电压响应仿真值
3.3 密排指向性影响
两列长轴密排换能器阵在不同间隔下谐振点的指向性情况见图20。图21是与之对应的仿真结果图。从图中可以看出,随着间隔的不断减小,换能器阵的指向性由“8”字形逐渐向全指向性转变,与理论仿真一致。
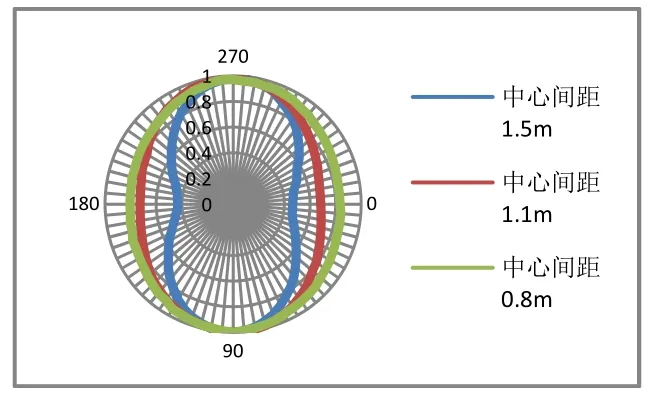
图20 不同间距下谐振点指向性实测值
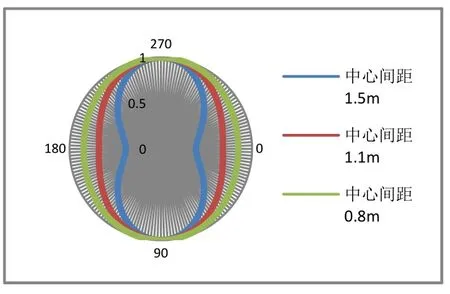
图21 不同间距下谐振点指向性仿真值
4 结论
通过对换能器密排成阵的仿真可以看出,密排布阵主要影响该排列方向的响应曲线。随着布阵间隔的减小,受到互辐射影响的作用,谐振点的响应值有所下降,增加了带宽,使得指向性由“8”字向全指向性转变,增大了波束宽度,同时高度方向和短轴方向小间隔密排还能有效地降低谐振频率。
本文将密排布阵形式对换能器响应的影响情况进行分析总结,可以为小尺寸下发射阵密排布阵提供参考。后续工作将开展从理论计算角度分析密排布阵对IV型弯张换能器性能的影响。

