混响水池声场特性研究及其建模分析

王少博

（第七一五研究所，杭州，310023）

混响声场是指在一定空间内，声场由直达声和反射声、散射声叠加的声场。混响室是空气声学研究中经常使用的实验装置，其理论发展较成熟。在混响室声模态方面，Richard Bolt[1]和Schroeder[2]等人在混响室声模态统计及模态密度方面作出了很多贡献，总结了如何计算频带内模态数量及满足测量精度要求的频率。1955年，Richard Cook[3]将统计分析应用于室内声学中，定义了两空间点均方声压的相关系数，其后很多作者通过混响声场的相关函数研究其特性。Morse、Ingard[4]等人研究了点源声场的理论及实验，结果表明通过改变点源的位置可以激励很多交叠的模态。

由于水池的反射系数较低，所以水下较难建立理想的混响场，而只有满足或近似满足扩散场特性（声能密度均匀）才能够进行声学测量。若能通过对混响水池声的研究，分析混响水池的声场特性，确定混响水池中扩散场的区域，对在混响水池中开展声学测量工作有重要意义。

1 混响水池声场特性分析

混响水池一般都有光滑的壁面，上表面敞开，无遮盖。声源在其中发射时，声波经各侧壁的反射、叠加，形成了混响声场。假定混响水池为矩形，长、宽、高分别为lx、ly、lz，如图1所示。

图1 混响水池示意图

1.1 波动声学分析

1.1.1 矩阵非消声水池内的简正波

用直角坐标系表示的波动方程为：

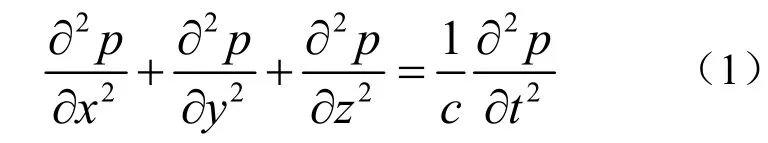
把坐标原点取在水池的一个角上，可以写出理想水池壁面的边界条件为：

满足上述边界条件的特解为

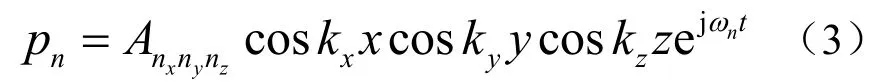
相应的每个特解的特征频率（简正频率）为：

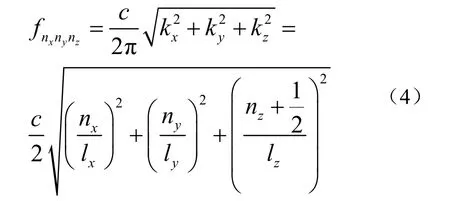
对应每一组（nx,ny,nz）数值的特解就决定了一种平面驻波，水池内的总声压就是所有特解的线性叠加。根据式（4）得到矩形水池的前20阶简正频率如表1所示。

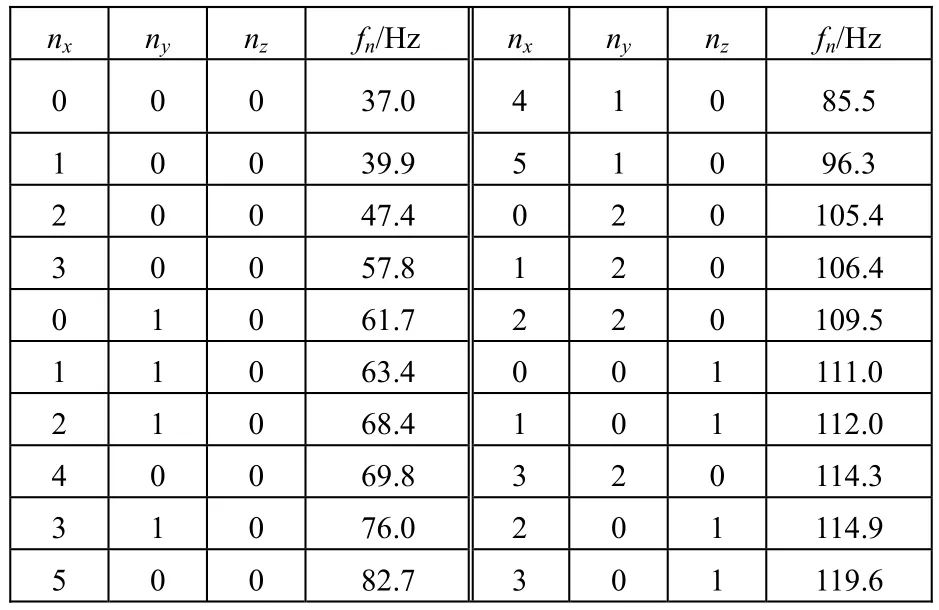
表1 矩形水池50m×15m×10m前20阶简正频率

通过建立波数k的直角坐标系，可以估计得到频率低于f的简正波总数为：

将式（5）对频率进行微分，可得在df内的简正频率数：

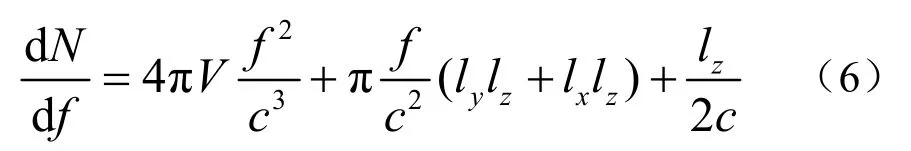
式（6）表明在频率f附近的df频带内的简正频率数基本上与频率平方成正比，随着频率增高增加得更快，因而当频率较高时，大量简正波的叠加可以把驻波效应“平均”，而使室内声场趋向均匀。

1.1.2矩形非消声水池内点源声场分析

根据Morse室内声学理论[4]，在点r处由r0处的简单声源所产生的声压可以由特征函数（即1.1.1中波动方程的特解）的级数表示，稳态声压的级数解为：

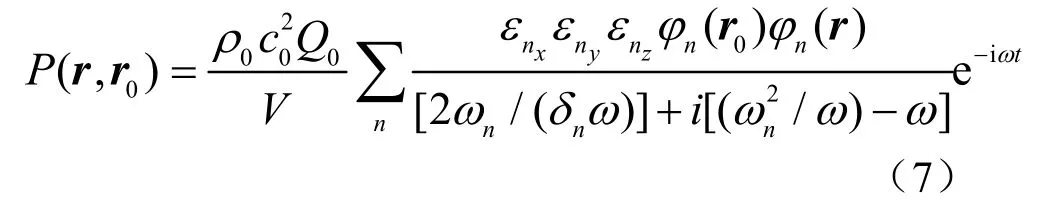
式中，V是混响水池的体积；φn(r)为矩形水池中第n简正波的本征函数；ωn为简正模态的频率；δn为声能的衰变率，等于每秒衰减的奈培数，反映了φn(r)的衰减特性。

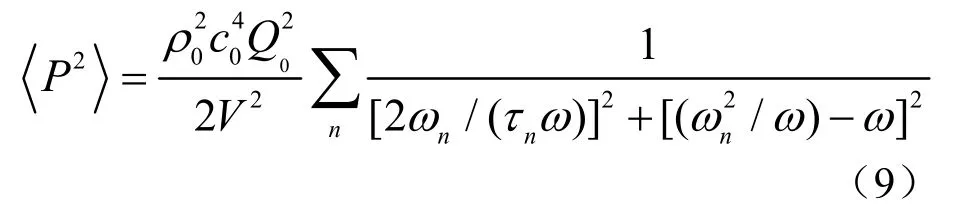
上述公式表明，在混响水池内对水听器的灵敏度进行校准时，对水听器及声源进行空间平均，可以降低混响水池中简正波所带来的影响，提高测量精度。

1.2 统计声学分析

混响水池的声能由两部分组成：一是直达声，二是混响声能。叠加声场的总平均能量密度应为：

式中，括号中前一项表示直达声的贡献，后一项表示混响声的贡献。当时，直达声与混响声的大小相等。此时有临界距离

当r＞2rh时，混响声比直达声大6 dB，直达声的作用可忽略，可以定义此区域为混响控制区。为了提高信噪比，通常取r＞4rh（混响声比直达声大12 dB），即

房间常数R0，定义如下：

式中，S为水池的壁面总面积，为平均吸声系数。

同时由文献[4]可知混响时间T60可以由下式表示：

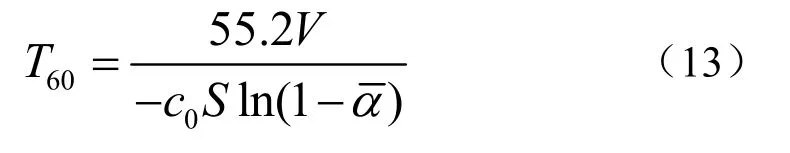
联立式（12）、（13），可得：

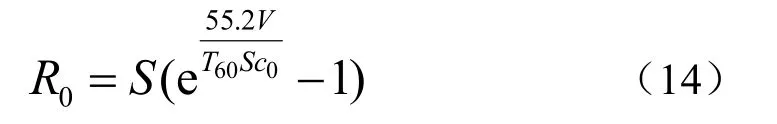
即可以通过测量混响水池的混响时间T60来得到扩散场区域距离声源的距离r。另外扩散场区域离壁面距离＞λ/4。

2 混响水池声场特性的建模分析

建模分析采用LMS Virtual Lab Acoustics软件[5]，这是专门用于声学分析的CAE软件，基于Sysnoise发展而来，不仅继承了Sysnoise的功能，还发展了快速多级边界元（Fast Multipole-Boundary Element Method，FM-BEM）技术、有限元自动匹配层（Finite Element Method-Perfect Matched Layer/Automatic Matched Layer，FEM-PML/AML）技术、时域边界元和有限元（Time Domain-Boundary Element Method/ Finite Element Method，TD-BEM/FEM）技术、自适应声学单元（Finite Element Method with Adaptive Order，FEMAO）技术、声线法（RAY）等。通过FEMAO技术可以在降低建模精度的条件下保证计算精度，缩短了计算时间。

计算目标为混响水池，长宽高分别为 50 m、15 m、10 m。水池上表面为水-空气界面，水池壁面及底部为混凝土结构，其密度为ρ=2.4×103kg/m3，杨氏模量E=1.7×1010N/m2，泊松比σ=0.21，由此可计算得到声波在混凝土中的纵波传播速度为c=2 824 m/s。取水的密度为ρ0=1.0×103kg/m3，声波在水中传播速度为c0=1 480 m/s，可求得壁面及底部的垂直入射反射系数为R=0.67。因此水池模型壁面及底部反射系数为 0.67，上表面为空气阻抗 416 kg/(m2·s)。

2.1 混响水池点源声场分布计算

首先计算混响水池的声模态，即简正频率的计算。nx=2、ny=2、nz=0时的水池声模态图如图2所示，此时简正频率f=109.5 Hz，同表1理论计算结果相吻合。图中红色区域表示驻波的极大值点，蓝色区域表示驻波的极小值点，nx=2表示在x方向上的驻波有两个半波长。基于声模态计算混响水池的点源声场，点源设置在距离水池左侧壁面5 m处的中心位置，100 Hz时的水池声场分布图3所示，在距离声源较近处，声场较为复杂，在距离声源较远处，声场起伏较小，近似满足扩散场条件。

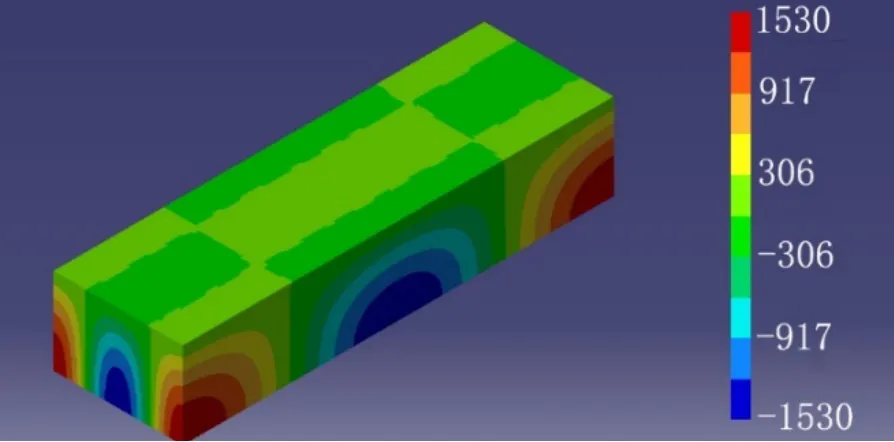
图2 nx=2、ny=2、nz=0时的水池声模态（f=109.5 Hz）

图3 100 Hz时水池声场分布

2.2 散场区域确定

由1.2中理论推导可知，确定混响水池扩散场区域需要混响水池的混响时间，由于模型尺寸较大，故采用声线法进行计算[5]。水池模型如图4所示，灰色网格为水池边界。图中橙色矩形网格是场点网格，距离水池上表面5 m，相当于距离上表面5 m处的剖面。点源距水池左侧壁7 m，距上表面5 m，距前壁面7.5 m。

图4 水池模型图

通过计算得到100 Hz时水池混响时间T60分布如图5所示，由图可知，距离点源较远处（大于20 m）的混响时间约为0.135 s，根据1.2节推导的公式可得r≥31 m处为混响控制区（同时距离壁面及表面应有一定距离）。

图5 混响水池T60分布

100 Hz时水池声场分布如图6所示，为垂直于z轴的声场剖面图。由图可以看出距离声源约31 m处有较大区域声场稳定，可以认为此区域为混响控制区。200～400 Hz时有类似结果。

图6 混响水池声场剖面

3 结论

本文首先通过波动声学理论和统计声学理论分析了混响水池的声场特性，然后通过仿真建模验证了混响水池的特征频率，并确定了扩散场区域。通过建模分析对于长宽高分别为50 m、15 m、10 m的混响水池来说，距离点源25～35 m的范围内声场较为均匀，近似满足扩散场条件，为进一步实验研究提供了参考。对于混响水池的理论分析，本文只分析了刚性壁面的声场特性，对于非刚性壁面还需要进一步推导。