新建住宅与二手住宅价格指数关系的研究分析*

丰 茂 芳

(南京财经大学 应用数学学院，南京 210046)

0 引 言

自20世纪90年代以来，我国的房地产市场总体来看虽有一定的波折，但持续性的投资，使其得到了快速的发展和壮大。我国取消住房实物分配制度后，居民的住房主要通过房地产市场解决，新建住宅成为房地产市场的主体，加之房价的过快上涨、供求矛盾、住房结构不合理等问题不利于居民住房需求的满足，政府也在房地产发展过程中通过宏观调控抑制房价过快上涨和打击投机性需求的行为[1-3]。高涨的房价已经超出了很多消费者的承受能力，使得很大一部分消费者只能“望房兴叹”，消费者对二手房的观念也在逐渐发生改变，刚开始二手房交易量比重偏低，但随着我国经济的高速发展和城镇化进程的加快，二手房交易的比例逐年提升。

由于我国房地产企业十几年来发展速度迅猛，所以发展过程中显现出来很多问题，例如：房价泡沫不断被挤压的问题，从市场角度对数据进行分析，或从房价指数的同比数据来看，继续保持正增长，但增幅都有所收窄。需注意，部分城市的房屋销售其实是有所上升的，所以能够有效把控房价增幅。而从同比增幅数据看，继续合乎预期，进一步收窄，充分体现了持续的房价管控使得房价的同比增幅不断变小，尤其是部分大城市同比增幅已经快速收窄。从城市当前房价指数的增幅来看，出现的房价环比下跌，具有极为重要的信号意义，充分说明了当前此类城市房价的泡沫不断被挤压。针对一手房和二手房市场关系的研究文章比较少，不论是政府还是社会对二手房市场的关注度都比较低，而二手房市场作为房地产市场的重要一部分，其在房地市场发展中具有不能轻易忽视的作用，根据相关理论，房地产市场越成熟，则二手房的交易比例就越高[4]。

1 非参数估计方法——核密度估计

在统计学中，往往需要根据样本数据去推断总体的分布，即密度函数。如果采用参数估计的方法，则要先假定总体分布的具体形式，如总体服从正态分布N(μ，δ2)，然后利用样本数据去估计参数μ和δ2，从而得到总体的密度函数。但若真实总体与假定分布相差甚远，则根据参数估计法得出的统计推断可能具有较大偏差。而非参数估计[5]的方法可以在不假设总体分布的情况下进行密度函数的估计，从而降低误差。

选取非参数估计中的核密度估计对新建住宅和二手住宅的销售价格指数进行密度函数估计，其步骤一般为：选取核函数；计算最优带宽；进行核密度估计。

1.1 核函数

核密度估计[6]是由Rosenblatt(1956)和Parzen(1962)对直方图作密度估计的思想推广而来，直方图作密度估计时，即使随机变量是连续的，直方图也始终是不连续的阶梯函数，而核密度估计可以解决这一缺点，从而得到密度函数的光滑估计。其核心是采用一个光滑可微的核函数。核密度估计量为

其中，函数K(·)称之为核函数，h称为带宽。满足以下性质：

(Ⅰ)K(·)连续且关于原点对称；

(Ⅲ)① 存在z0>0，当|z|≥z0时，K(z)=0，或② 当|z|→∞ 时，|z|K(z)→0；

条件(Ⅱ)要求核函数的曲线下面积为1(将核函数标准化)，并满足一些有界条件.条件(Ⅲ)下①比②更强，在实践中尝尝采用条件①，即如果超出某个邻域范围[-z0，z0]，权重变为0。常将[-z0，z0]标准化为[-1，1]。条件(Ⅳ)也是一个有界条件。

现给出常见核函数，见表1：

表1 常见的核函数

如表1所示，常用的核函数主要有上述几类，其中，均匀核也用于直方图，只是在用均匀核进行核密度估计时并不固定分组，而在每个点上进行估计。最流行的核函数为二次核与高斯核。条件(Ⅲ)下除高斯核满足②外，表1中的其他核函数均满足①。这些核函数的共同特点是，离原点越近，核函数的取值越大，并在原点处取得最大值，这意味着，越近的点给予的权重越大。

1.2 最优带宽

其中：

则可以改写成

然而均方误差依赖于每一个观测值，若希望对x所有取值的均方误差进行整体度量，则可以最小化积分均方误差(IMSE)，

为求解minIMSE(h)，Silverman(1986)证明最优带宽为

从表达式可以看出，最优带宽h*依赖于δ从而依赖于核函数，还依赖于待估密度函数的二阶导数f″(x)。

若样本来自于正态总体，则可以计算出h*=1.364 3δN-0.2s，其中s为样本标准差。为了防止样本标准差受极端值的影响，常使用Silverman嵌入估计，可得

h*=1.364 3δN-0.2min(s，iqr/1.349)其中，iqr为样本的四分位距。

在实际操作中，即使整体不服从正态分布，也可以使用嵌入估计来进行带宽的选择，但为了保险起见，可以比较两倍嵌入估计与一半嵌入估计的效果。

2 新建住宅与二手住宅销售价格指数的比较

2.1 数据说明

为保证数据的可得性、科学性和研究的可能性，选取数据来源于国家统计局，选取了全国70个大中城市，从2017-01—2017-09关于新建住宅和二手住宅这9个月的价格指数(同比)作为对比数据，价格指数是反应不同时期一组商品(服务项目)价格水平的变化方向、趋势和程度的经济指标，是经济指数的一种，通常以报告期和基期相对比的相对数来表示。按其计算时采用基准期的差别，可以分为环比价格指数、年距环比(同比)价格指数和定基价格指数，选取的是同比价格指数。将新建住宅和二手住宅的价格指数(同比)分别表示为样本fhouse、shouse，单样本容量为630，总样本容量为1 260。数据分析软件选用R。

2.2 住宅价格指数的基本数字特征

首先，对两类样本fhouse，shouse的一些数字特征进行描述，见表2：

表2 两样本的数字特征描述

由表2所示，两者之间均值相差不大，相对来说，二手住房的标准差比新建住房标准差大，说明二手住房之间的价格指数波动范围相对于新建住房的价格指数波动范围比较大，由此进一步的表明随着新建住房价格的居高不下，二手住房价格波动比较大，不稳定，越来越多被消费者所接受。

2.3 住宅价格指数密度曲线的核密度估计与分析

在对两类住宅的价格指数做核密度估计之前，先对两种房屋做频率直方图：

如图1所示，新建住宅的价格指数(同比)在区间[105，110]之间频数最大，二手住宅的价格指数(同比)在区间[100，105]之间频数最大，而两类住宅在区间[100，110]呈现频数表现最大，说明两类住宅的价格指数(同比)大多集中在该区间内，但是二手住宅落在区间内的频数超过250，而新建住宅的价格指数(同比)大于200，说明二手住宅销售价格有更大的概率指数稳定在区间内，价格指数(同比)频数主要分布范围在[100，115]之间，说明与上一年的同月的销售价格指数都在区间内，还可以看出，新建住宅的价格指数变大，相应区间的二手住宅的价格指数变小，两者之间存在着相互关联性。

图1 两类住宅的频率直方图

由于核函数K(·)在进行核密度估计时对结果影响不大，选取epanechnikov核。用文中提到的Silverman嵌入估计得到新建住宅的价格指数(同比)对应最优窗宽，二手住宅的价格指数(同比)得到最优窗宽。

下面将两组数据得到的最优窗宽及两倍与一半的窗宽带入进行核密度估计，估计结果见图2：

如图2所示，两累价格指数通过使用嵌入估计求得最优带宽，此时进行核密度估计可以得到更光滑的核密度估计图像。且可以看出新建住宅和二手住宅的价格指数均呈现右偏尖峰分布，说明二者价格指数集中在一个值106(较高的价格指数)的附近。从而说明新建住宅和二手住宅的价格指数相对具有一定的稳定性，通过观察二者的价格指数的原始数据所对应的时间节点发现，价格指数呈现相对的波动性，一个变化大小影响另一个变化的多少。

下面是对全国70个大中小城市两类住宅在2017年9个月中的价格指数(同比)核密度的估计比较情况，见图3：

图2 窗宽的选择与比较

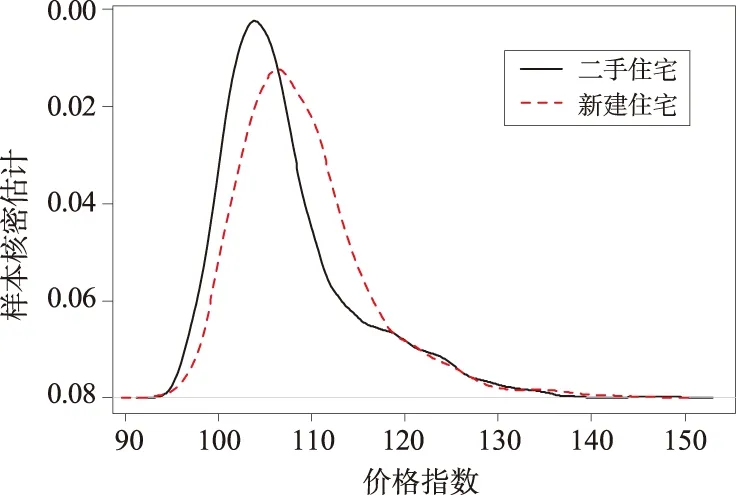
图3 两类住宅销售价格指数的核密度估计比较

如图3所示，对2017年9个月住房价格指数的核密度估计中发现：(1)两者的价格指数密度曲线的核密度估计均表现为右偏尖峰分布，即二手住房的价格指数的核密度函数值较大，新建住房的价格指数的核密度函数值较小，说明二手住房对应的价格指数概率密度曲线更高，集中分布在价格指数105值的附近；(2)新建住宅和二手住宅价格指数密度曲线的核密度估计整体不断右移，说明我国现今住房整体在不断提高，随着房价的不断飙升，销售价格涨幅一直处于核密度曲线的峰值106左右，经济快速增长，带动房产业市场快速发展，房价的高涨使得人民的收入无法支付[6]，故消费者转变目光开始关注二手住宅市场，购买二手住宅；(3)在价格指数为110之后，新建住宅的核密度函数值总体上大于二手住宅的核密度函数值，说明当价格指数偏大时，消费者更倾向于购买新建住宅[7]。

下面对前3个季度的两类住宅销售价格指数(同比)的比较分析，见图4：

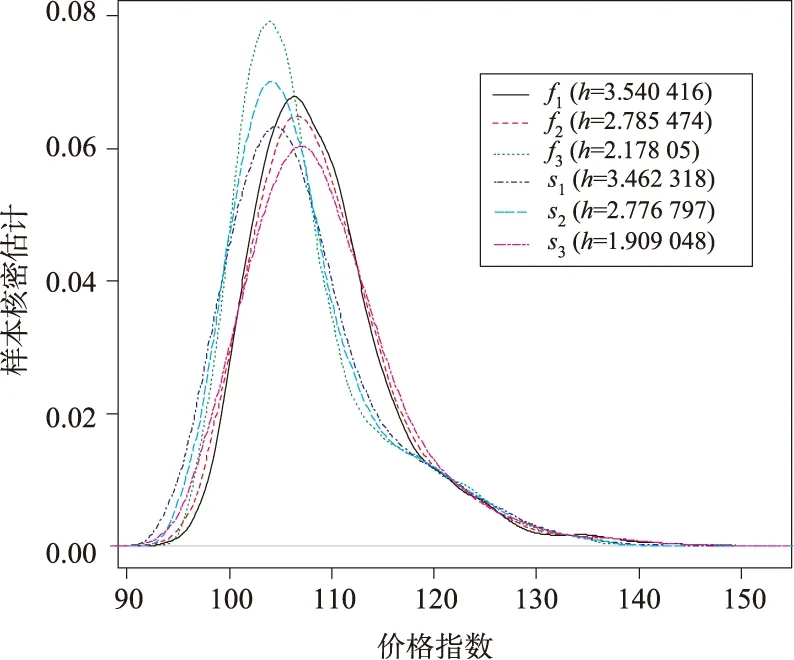
图4 前3个季度两类住宅的销售价格指数比较

如图4所示，对3个季度的新建住宅和二手住宅的价格指数做的核密度估计，其中f1，f2，f3分别表示新建住宅的第一、二、三季度，s1，s2，s3分别表示新建住宅的第一、二、三季度，首先看第一个季度，新建住宅的销售价格指数与二手住宅的价格指数呈现相同的趋势，数据主要集中数值在108的位置，此时两类住宅的销售状况相互影响不大；第二个季度二手住宅的销售价格指数明显比新建住宅的销售价格指数变大，且价格指数值处于105附近，而新建住宅的销售价格指数值处于108附近，由此可知新建住宅变动极大地影响了二手住宅；在第三季度中，两类住宅销售价格指数出现了巨大差异，新建住房的价格指数的核密度函数值远远大于二手住房的价格指数的核密度函数值，说明在此期间，新建住房的销售价格指数比重较高，二手住房的销售价格指数比重较低。

3 结论及建议

从核密度估计图中可以看出，二手住宅需求与新建住宅的需求大体上一致，两者存在关联性[8]，二手住宅价格以新建住宅的销售价格为风向标，二手住宅的销售价格涨跌通常与新建住宅价格保持一致。区别在于在当下二手住宅的投资投机性需求较少，大部分二手住宅购买者主要为了解决住房问题。目前我国二手房价格总体来说低于新建住宅，这对经济条件相对有限的消费者来说具有较大的吸引力[9]。此外，对于急需入住的消费者，二手房是他们的首要选择。以前价格因素、政策变化和消费观念对二手房市场影响很大，尽管二手房价格要比新建住宅低得多，但是由于对二手房不放心的因素，导致我国二手市场的发展落后于发达国家[10]。现今随着社会的迅速发展，人民观念开始改变，对二手房也越来越青睐，特别是学区房，可以看出未来的二手市场发展的空间较大，在未来的购房需求中，二手房的需求会逐渐加大比重。

采用非参数方法中的核密度估计方法对新建住宅和二手住宅的价格指数进行核密度估计，让消费者了解到新建住宅和二手住宅在房地产市场中是息息相关的，也能为政府在调控新建住宅的同时考虑政策对二手住宅的影响，加强引导消费者的购房行为回归理性，并通过对一手房市场的调控间接地引导二手市场的进一步发展。