乾嘉算学家对借根方与天元术看法的转变

魏雪刚

(中国科学院自然科学史研究所，北京 100190)

东西文明的遭遇与冲撞是科技史研究的一个取向，西算在中国的境遇又是清代算学史重要且有趣的话题。就借根方来说，它经历了从传入宫廷而被接受，到被收入《数理精蕴》而广为传播，又到中算家受其助力而掌握天元术，再到中算家对借根方和天元术看法的转变等等，这一切值得我们进行具体而微的研究。韩琦考察了借根方的传入与乾嘉古算的复兴[1—2]。本文尝试在此基础上，从算法的视角出发，对借根方在乾嘉时期的具体遭遇展开进一步的讨论。

1797年春，李锐(1769—1817)校《测圆海镜》完成，这是一大关节处[3]，在此之前，算学家对借根方有较高的评价，在此之后，多数算家虽仍认为借根方有很高的价值，他们却转而倾向于天元术。中算史家多注意到了这一转变，就其转变的原因，洪万生、刘钝从乾嘉学派与算学的关系展开论述[4—5]，田淼从择善而从的角度进行分析[6—7]。他们的研究颇具启发性，不过我们认为这种转变的原因极为复杂，需要从多个角度来讨论。因此，我们在重新考察相关问题的基础上，力图寻找更多的原因，却始终未曾想对此问题做一全面而完备的回答，这或许也是根本不可能的。

1 乾嘉算学家未接触到的借根方内容

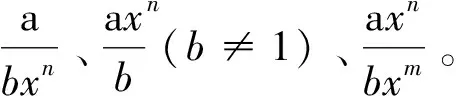
而在中算家看来，寄母和正负开方法却是天元术优于借根方的关键(3)事实上，中算家对寄母的重视渊源有自，《张邱建算经·序》：“学算者不患乘除之为难，而患通分之为难。”李籍《九章算术音义》：“能治诸分，则数学之能事尽矣。”阮元《畴人传》卷六“张邱建”条：“之分之术明，则《九章》之要一以贯之。”。如阮元(1764—1849)所说：

“西法之所自诩者，用八线推三角角度暨借根方而已。不知借根方即天元一，而较逊于天元一，以不善寄母兼不善古开方法，故三乘方已上与夫正负杂糅之方，皆借根之所穷。而三角八线未见于天元一，习西法者遂疑天元亦于此有穷。茗香罗君则谓元人之书所以不驭此者，彼时三角法未入中土也。”[11]

罗士琳(1774—1853)为了说明天元无穷，专门写作了《三角和较算例》一书。

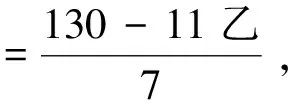
其实，《借根方算法》中的未知数表达形式并不限于“根”“方”，且不限于“甲”“乙”二字，正如题中双行夹注所言：“此法内用甲、乙、丙、丁字，不用根数。”这里选择天干表达未知数，具有明显的符号化特征，若把天干换成现代数学中的x、y、z也未尝不可。《借根方算法》上卷之二和上卷之三有大量用天干表示未知数的例子，但其指数均为1。看来，《借根方算法》中的借根方也可解决多元一次问题，而天元术(四元术)则不能解决五元以上的题目。同样可惜的是，《借根方比例》未收录这种天干表示法(4)明安图《割圆密率捷法》卷三“分弧通弦率数求全弧通弦率数”注云：“借根方法任借数根俱可，故古法有立天元一、地元一、人元一者，《四元玉鉴》又有所谓四元者，皆此类也。”看来明安图对借根方未知数表达方法的理解更接近《借根方算法》，但这未在当时产生影响。。

如此看来，乾嘉算家未能见到借根方的本来面貌，忽略了不少关键要素，以致它的优势无法在当时发挥出来。算家正是在这种情况下来讨论借根方与天元术的异同问题。

2 中算家对借根方与天元术异同的比较

乾嘉算学家对借根方与天元术的异同多有辨析。梅瑴成(1681—1763)的《赤水遗珍》就是这样。该书用借根方解释天元术[12]，具体而言，借根方等式两侧均不为零，即f(x)=g(x)；天元术相消后得到开方式，形式类似于f(x)(或f(x)=0)。就各项的正负而言，相消前后两种形式是有差别的，梅瑴成并不关心这种差异。“余勾余股求容圆径”问得到负平方、负一次方、正常数的开方式后，梅瑴成注曰：“则右余一天元幂与左余九万六千少八十根相等也。”([13]，页13a)其中，平方的正负相反。不仅如此，他还用天元术的术语解释借根方。“有弦与积求勾股”问先借根为勾，后得一等式：676x2-x4=57600。这被描述成正实、从廉、负隅，然而按照天元术的方法，这只能是正实、负廉、正隅或负实、从廉、负隅。随后的开方却采用了“负隅、益积三乘方”法，不知梅瑴成是否留意到这里的矛盾。这个缝隙在乾嘉时期有很大的影响。梅瑴成对朱世杰的评价不高，原因有二：一，《四元玉鉴》“或问歌彖”第一问用“正隅”“从隅”两词指代正二次方，梅瑴成称这是“故异其词”([13]，页16a)。二，“或问歌彖”第三问求勾股时，因天元术左右可以互消，即f(x)=0可以转化为-f(x)=0，同时用了这两种形式，梅瑴成却感慨道：“何以参差如此乎？”([13]，页18b)。看来梅瑴成对天元术的了解并不深入。

李锐认为借根方不如天元术“简且易”([10]，李锐跋)，并在《测圆海镜细草》中批评馆案“惟知借根方法”([10]，卷三，页13b)。馆案受《赤水遗珍》的影响较大，如用天元术术语解释借根方。《细草》卷六第十二问“有草无法”，馆案补法用实、从、廉、负隅指代等式35200x+21504000=640x2-0.5x3各项，这与梅瑴成对天元术术语的误用如出一辙。对此，李锐提出了异议，“廉当云益廉，负隅当云隅。盖加减所得多少，与相消所得正负相反也”([10]，卷六，页11a)。这种看法是正确的。

李锐进而比较了借根方与天元术的异同([10]，卷二，页12b—13a)。借根方用“加减法”化简后的形式是f(x)=c(c>0)，天元术用“相消法”化简后的形式有两种f(x)-c=0(c>0)或0=c-f(x)(c>0)。若天元术常数项为正则两术中f(x)各项正负相反，若天元术常数项为负则两术中f(x)各项正负一致。李锐虽然指出了梅瑴成天元术术语使用的错误，却没注意到相消法与加减法在算理上的一致性(5)关于李锐的天元相消法，可参考：洪万生.《无异解》中的三案初探：一个HPM的观点.科学教育学刊，2000，第八卷第三期，215—224；郭世荣.中国数学典籍在朝鲜半岛的流传与影响，山东教育出版社，2009∶144—151.。此外，李锐强调相消“可以又数减寄左数，亦可以寄左数减又数”([10]，卷二，页12b)。这其实点明了天元开方式的正负可以整体互换，反驳了梅瑴成对朱世杰的批判。

焦循(1789—1820)赞同李锐借根方与天元术之殊的看法，但在天元相消问题上与之有间([14]，焦循序)。他说：“借根之用加减，与相消法异而数同……盖两边各减，仍不啻以左减右。”([14]，下，页24b)并用一个算术式来说明：有5+5=10，左侧+5为“多五”，相消法为5=10-5，加减法为(5+5)-5=10-5，两法结果均“相等”。相消得到的开方式，在这里竟成了等式，且两端均不为零，如其所说：“相消必分两畔者，缘两畔之相等也。”([14]，下，页24a)“两畔”除了具有等式两侧的涵义外，还表示开方式的各项按盈朒或和较所分成的两类。若把开方式表示为f(x)-g(x)=0，则f(x)和g(x)也为“两畔”。

焦循坚信天元相消不与直除同而与盈朒理同(6)关于盈朒与借根方的关系有很多论述，《借根方算法》认为借根方算题“用叠借、互徵法可以类推”。《数理精蕴·叠借互徵》把盈朒比作叠借互徵。《借根方比例》认为借根方“大意与借衰、叠借略同”。《里堂学算记·阮元序》称：“借衰即衰分之列衰，叠借即盈不足之假令。”，理由是“方程之直除，可同减异加，亦可异减同加。惟盈不足则止可同减，不可异减；止可异加，不可同加，天元一之相消亦然”([14]，下，页28a)。关于直除，骆腾凤(1770—1841)、安清翘(1759—1830)等算学家也有相同的认识。这里讨论的重点在加减，焦循有进一步的论述，“方程两色各备和较，故可以异加，亦可以同加，和较备则消息相通也。天元一本消之前，有和而较不备，其寄数、又数两列，不啻盈不足之有出率、有差数，故止可异加，必不可同加，亦如盈不足之必用同减异加也”[15]。这就是说，和、较备与不备是方程、盈不足、天元三术的差异所在。和、较概念的使用显然受到了梅文鼎(1633—1721)《方程论》的影响，其实就连所谓的“两畔”及对盈不足和方程术的关注，也都与梅氏密切相关。

骆腾凤声明了他与李锐的差异：“李氏谓借根方出于天元一术，其加减乘除之法并同，惟此相消法与借根方两边加减有异，不知借根方之异于天元一者，在正负多少之异，不在两边加减之异也。”([16]，卷一，页36b)他所谓天元术的正、负并没有实际意义，只是用来别同异、定加减的。借根方的多、少却对应着盈、朒，具有实际意义([16]，卷一，页38a—40a)。他还比较了两者加减运算时的差异，“四平方多四根与二平方少三根相加”问中借根方需要解释下式的实际含义：(4x2+4x)+(2x2-3x)，即“则于多四根内反减少三根，而多数大，仍为多，是为六平方多一根，盖名为加而实减也”([16]，卷一，页39a)。这继承自《借根方比例》。天元法则先变号后加减：4x2+4x+2x2-3x，即“则四正平方、四正元与二正平方、三负元相较，则同名相加，得六正平方；异名相减，得一正元矣”([16]，卷一，页39a)。由此，骆腾凤认为借根方窒碍，天元术直截了当。事实上，这种难易程度的不同主要由直观解释与符号化的差异所致。吊诡的是，二者这方面特征在此互换了。这种先变号的方法，使得天元术只能“同加异减”。骆腾凤对多、少的解释受到了焦循的影响，《开方释例》用天干表示大小数即来自《加减乘除释》[17]。焦循用“两畔”相等说明天元相消结果的做法，也被他采用了，如把“一立方多十三平方多三十根与二万七千一百四十四尺等”说成“正隅一、正廉十三、正方三十与负积二万七千一百四十四等”([16]，卷一，页38b)。

骆腾凤在“方城圆城求径法”中批评李锐：“惑于正负多少之说，而不知正负可以互用，遂以两边加减为误，其为不知天元法也，一而已矣。”([16]，卷一，页60b)此问为《测圆海镜细草》卷三第十题，原文求出天元开方式后，馆案用借根方等式把它翻译了一遍，使得常数项或根方项的正负有变。李锐对其用借根方解释天元术一事提出异议。李锐其实已明言天元开方式正负可以互换，骆腾凤的批判是不合理的，这与他滥用“正负可以互用”原则有关。事实上，骆腾凤念兹在兹的是，“正负者，加减之谓，非多少之谓也”([16]，卷一，页36a)。这里对正、负的看法是合理的，对多、少的看法有失偏颇，因为从《借根方算法》到《借根方比例》“多、少”一直都是“加减之谓”。造成这种误解的原因当然与焦循有一定的关系，但更主要的是：一，借根方用易与“大、小”相混的“多、少”来表示正负。二，《借根方比例》追求直观解释，“多、少”被赋予了实际意义。有趣的是，张文虎带着更大的误解把正负比作盈朒，并以此来批判骆腾凤“异在正负不在两边加减”的说法[18]。

汪莱(1768—1813)一直坚持使用借根方，他认为“夫天元一相消之后，其数已无，以其无数求其有数，非初学所易会。借根方相等之后，其数相对，以其对数寻厥真数，岂浅人所难解？”[19]这里的比较也集中在相消法与加减法的差异上。借根方加减之后等式两侧仍有“数”，天元相消则等式消失，开方式就不存在对应的“数”了。

安清翘《学算存略》、张作楠(1772—1850)《翠微山房数学》也有相关讨论，主要观点不出以上所述。

总而言之，乾嘉时期中算家的关注点较为集中，即相消法与加减法、正负与多少。事实上，他们并未抓住借根方与天元术异同的关键所在，如都可归为一元多次方程问题，如表达方式的区别，等等。究其原因：一，对相消法与加减法关注可以追溯到梅瑴成的《赤水遗珍》，对正负与多少的关注体现了符号化与直观解释取向的不同。二，算家无论对借根方还是对天元术都存在一定程度上的误解。三，梅文鼎《方程论》扮演了重要的角色，李锐对直除只可用减的看法、焦循和较概念的使用都与之有关，此二人的观点又在当时发挥着统领性的作用。

3 学术背景：古算的发掘与研究

自从乾隆下诏开设《四库全书》馆，古代算学著作陆续被发现、整理与研究。天元术被再次理解，焦循在给李锐的信中，说出了他对当时天元术和借根方的观察：“窃谓天元一之法，晦之已久，而西人借根法，学习者亦少。兄更宜推而详之，以彰明此绝学，弟所深望也。”[20]

中算家曾一度把秦九韶的大衍术、李冶的天元术混为一谈，认为李冶的天元术来自秦九韶。钱大昕(1728—1804)《数学九章·跋》及焦循《天元一释》都专门辨析了大衍术与天元术的异同，自此它们才被区分开来。焦循、李锐、张敦仁(1754—1834)、骆腾凤还都对大衍术进行了阐释[21]。

“谈天三友”是天元术复兴的功臣，焦循多次谈到他要使古学显著于海内，李锐也说：“锐于算学未有深得，而笃好立天元术，亟欲章而明之，则颇与里堂相似。”([14]，李锐序)焦廷琥(1782—1821)称：“秦、李之学所以复明者，府君与汪、李两先生证订之力也。”[22]

乾嘉时期中算学家反复强调开方术的重要性。他们多是通过《数理精蕴》才接触到借根方的，该书说：“借根方比例法中，开各乘方为最要。”([23]，下编卷三十二，页2)张作楠对借根方有所坚守，他的《量仓通法》重复了这种说法。阮元说：“少广著开方之法，方程别正负之用，立天元一者融会少广、方程而加精焉者也。”([10]，阮元序)这一说法在当时产生了不小的影响，易之瀚《开方释例》重述了这段话。罗士琳更是直接说：“不明正负开方者，不足与言天元。”[24]汪莱与李锐还在方程论问题上取得了很大的成就。

梅文鼎《少广拾遗》就是开方类的著作，自从乾嘉时期正负开方法被重新理解之后，中算家已经认识到了梅氏开方法的不足，对其多有微词。焦循明确地说：“梅勿菴《少广拾遗》发明诸乘方，于正负加减之际，厥而未备，故其廉隅繁琐，步算既艰，亦且莫适于用。”[25]由李锐《开方说·黎应南跋》和易之瀚《开方释例》可以看出，对中算家来说，正负开方法的优势主要体现在更具算理、更程式化两方面，这是借根方开方法无法相比的。张作楠虽然赞扬借根方查表法“简捷精妙，冠绝古今”[26]，但影响有限。

四元术相较于借根方有一定的优势，如可以解决不超过四元的多次问题。朱世杰《四元玉鉴》发现较晚，《畴人传》未提此书。嘉庆初年阮元在浙江访得《四元玉鉴》之后，嘱李锐校算，可惜李锐未完成就去世了。沈钦裴、罗士琳、徐有壬(1800—1860)、戴煦(1805—1860)也都研究过四元术。罗士琳《四元玉鉴细草》一书用了十多年的时间才完成，影响最大，虽然这样，却是沈钦裴的细草更符合朱世杰的本意[27]。

《九章算术》卷八为方程术，其中，消法可加可减；正负用来别同异，无实际涵义；正负用法有序，没有混乱的情况。此后，吴敬、程大位、李之藻、李笃培、李长茂、方中通等都倾向把正、负对应于正数、欠数，用焦循的话说就是，“元明以来，不知正负之旨。于是以空位立负，往往推之不可以通”[28]。不过，他们还是坚持方程消法可加可减这一原则。

梅文鼎看到了正负使用的混乱状况，他的《方程论》大有改旧弊的宏图，通观全书，他也确实做到了这一点，如其对正负的解释：“立正负以别同异，犹彼我也。”([29]，卷一，页15b)可是，在方程消法问题上，他却坚持只能用减，不能用加，焦循、骆腾凤、罗士琳都批评过这种看法(7)分别见：焦循《加减乘除释》卷五，页5b；骆腾凤《艺游录》卷二“方程正误”；罗士琳《续畴人传》“李锐论”。。梅文鼎的坚持与盈朒和阴阳观念有一定的关系，他说：“同名相减，即如盈朒章两盈、两朒相减也，异名相并即如盈不足相并也，岂有同加异减之理乎？”([29]，卷四，页9b)又说：“同名相减者，阴阳之偏，不得其配也。异名相并者，阴阳得类，雌雄相食也。是皆有自然之理焉，可以思古人立法之原矣。”([29]，卷一，页17a)

1676年，李子金(1622—1701)完成了《算法通义》，该书虽用正数、欠数解释正负，但对方程消法可加可减的认识及对正负的使用都是恰当的[30]。杜知耕《数学钥》(1681年)对方程的论述大体上出自此书。陈世明、屈曾发、屠文漪、吴兰修都对方程术发表过意见，与他们相比，却是戴震、李潢等校勘过《九章算术》的算家对方程术的理解更接近原意。

总而言之，天元术的发掘与整理是中算家态度转变的前提。算家认识到了大衍术和四元术的优势所在，这使他们更加坚信中算的价值，当然也包括天元术的价值。正负开方法与天元术密切相关，由第一节所引阮元语可知，它是天元术胜于借根方的关键之一。算家对借根方与天元术异同的比较与中算(如方程术、盈朒术)乃至更大的文化传统(如阴阳观念)有关。

4 观念的差异：对借根方的不同诠释

中西算家对借根方的诠释是不同的，这可从观念上的差异展开讨论。《借根方算法》重视借根方“设未知数”的特征，认为借根方与平常算法的差别在于前者“全以借根察所求之数”[31]，并用“相连比例数”(8)“相连比例数”对明安图、董祐诚、项名达等算家用“连比例率”来研究幂级数展开式有一定的影响。解释根方数的关系。书中虽有平方、立方、三乘方等术语，但它们与具体图形无关，只是用来描述数的类型。

1712年，法国耶稣会士傅圣泽(Jean-Francois Foucquet，1665—1741)为康熙写作《阿尔热巴拉新法》一文。该文认为新旧法的差异在于“旧法所用之记号，乃数目字样。新法所用之记号，乃可以通融之记号。如西洋即用二十二字母，在中华可以用天干、地支二十二字以代之”[32]。这无疑扩大了符号的使用范围，用天干表示未知数，用地支表示已知数，还用符号表示特定的对象。作者坚信“新法比旧法亦捷、亦简、亦总括、亦通融”[32]，“通融”即一般化，文中屡次提及。

然而，康熙否定了《阿尔热巴拉新法》，学者就其原因做过很好的分析[33]，此处提下我的浅见。康熙批评此书，“甲乘甲，乙乘乙，总无数目，即乘出来亦不知多少，看起来想是此人算法平平尔”(9)转引自参考文献[1].。这源于《阿尔热巴拉新法》原书：“单用字作加减乘除之法即毕，总无数目可见，似为无用。”[32]这里所说的新法没能计算出具体数值，有一定道理。其实此书开头就比较了算术法与新法的异同，算术式：12×12=144；新法式：(甲+乙)×(甲+乙)=甲甲+二甲乙+乙乙，甲、乙为满足两数和为12的任意正整数。可见算术法得到了具体数值，新法所求的只是解的结构，或者说是给出了运算程序，若想求出具体数值，还需再费一番功夫。傅圣泽无意于具体数值，运算至此就结束了。书中把系数全都用符号表示，其繁琐程度可想而知。傅圣泽明白若不求出具体数值，新法恐会沦为“无用”，但他追求的是由符号而达于通融，并不留恋于此。相较之下，康熙更在乎具体数值，在他看来只有如此才算最终解决了问题。

不难看出，符号应用范围的扩大是借根方发展的一个方向，晚清伟烈亚力对代数学发展历程的回顾可作为旁证，“是时，惟未知数用字代，已知数皆用本数。至肥乙大始尽以字代，是为今代数术之始”[34]。“肥乙大”即韦达(Franciscus Vieta，1540-1603)。韦达与前人的不同之处在于，他不仅用符号代替未知数，还用符号代替已知数，这就是伟烈亚力所谓“今代数”新之所在。

《借根方比例》则试图给借根方以直观解释：“要之，所谓一立方者即一正方体，而多平方、多根、少平方、少根即变正方体而为长方体、扁方体或为磬折长方体、扁方体。”([23]，下编卷三十三，页12)如此一来，脱离具体实意的天干符号就只好省略了。书中给出了带纵平方法的十二种不同类型的等式，并构造出了与之对应的几何图形。

《借根方算法》直接给出加减乘除的运算法则，不做过多解释。乘除法中用数值验证的步骤，只是用来保证运算法则的正确性，并不负责解释如此运算的原因。《借根方比例》则试着说明各法的实际意义，还有用图形解释乘法的例子。由于无法直观解释根方加减的实际意义，《借根方比例》对之避而不谈。

《借根方比例》认为三乘方不可知，梅瑴成《赤水遗珍》“圆田截积”则把其描述为“带一纵之长立方”，并画出了具体的图形([13]，页18b—20b)。其论证逻辑如下：因为x4=(x)·x3，若x的值为2，则x4=(x)·x3=2x3，此乃“两立方相接”，这就是说，三乘方的形状与x的值有关。带纵三乘方，因为x4+nx3=(x+n)·x3(n为自然数)，则x+n>x，所以纵“过于方根”。《同文算指》卷八“广诸乘方法”(10)钱宝琮主编的《中国数学史》认为《同文算指》开带纵平方与开多乘方等“没有超出我国古代数学的范围”(1964年，第237页)。严敦杰指出《同文算指通编》“十六乘通率”采Michael Stifel(1487—1511)的《整数算术》(Arithmetica Integera，1544)(李俨.《中算家的巴斯噶三角形研究》，《中算史论丛·第一集》，中国科学院出版，1954∶232)。潘亦宁在严敦杰的基础上认为，《同文算指》“广诸乘方法”底本为也来自《整数算术》。(潘亦宁.中西数学的会通——以明清时期(1582—1722)的方程解法为例[D].北京：中国科学院自然科学史研究所博士学位论文.2006∶42—46)但潘文未讨论多乘方图形解释法的来源，故此问题还需进一步研究。与焦循《乘方释例》《加减乘除释》都有类似的看法。这种解释有牵强的一面。

研读乾嘉算学著作会发现，即使像焦循一样痴迷追求算理，即使正负开方法已被重新理解与研究，中算家还是对直观解释情有独钟。就算是支持借根方最有成就的算学家汪莱也是如此，如其《衡斋算学》对梅瑴成的批评，如他对“可知”与“不可知”的考察。

可见，西方士人看重借根方符号化与算理的特征，中算家受中算重视直观解释的传统影响，更倾向用图形与算法来诠释借根方。这种差异导致中算家无法完全理解借根方。

5 结语

自从借根方传入中国之后，就遭遇了内容的缺失、误解、与天元术的比较或说是竞争、对其本意理解的偏差等等。在此基础上，我们看到了乾嘉算学家对借根方与天元术看法转变的复杂原因：一，天元术的再次被理解是前提条件。二，正负开方法、大衍术、四元术等与天元术密切相关，它们的发掘与整理使得天元术随之获得了更多的认可。以上两条又与编纂《四库全书》的社会背景密切相关。三，中算家对借根方和天元术异同的讨论，集中在相消法与加减法、正负与多少两个方面，未抓住问题的本质，这与中算及文化传统有一定的关系。四，中算家未能完全掌握天元术，这使得算理之外的因素更容易发生作用。五，借根方在传播过程中内容的缺失，导致它并非以全貌来与天元术比较。六、中算家对借根方的诠释与西方士人有差异，使得中算家未能完全吸收借根方的精义。当然还需加上学者已经注意到的原因，如从现代数学角度来看天元术在某些方面具有一定的优势，如乾嘉学派的影响等等。显而易见，社会背景、中算传统、思想观念等因素也都在这一转变过程中发挥着重要的作用，因而不妨把我们讨论的历程看作是，西方残缺的借根方遭遇到了中国的整个社会和文化。

致 谢本文承蒙业师韩琦研究员悉心指导，特致谢忱!