漫谈正多边形的尺规作图

徐惠杰

如何精确地作出正多边形呢？这是一个古老的几何问题.早在古希腊时代，人们就知道可以用不带刻度的直尺和圆规（尺规作图）作出几种正多边形.大家知道复杂的尺规作图都是由一些基本作图构成的，我们先一起探讨正四边形（正方形）的尺规作图的方法.

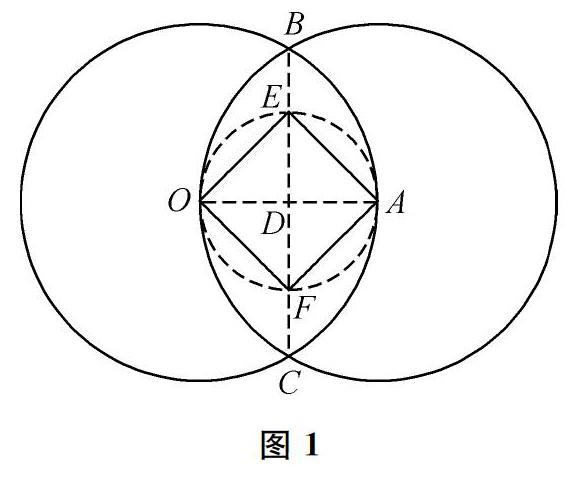
正方形该如何尺规作图呢？如图1所示，画圆○，作半径OA，以A为同心，OA为半径画圆，交于B，C两点，连结OA与BC交于点D，以D为圆心，OD为半径画圆交BC于E，F两点，则四边形OFAE为正方形，证明也较容易，

从上面的过程我们发现正方形的尺规作图还是比较容易的，但有关正五边形的尺规作图人们经历了一段探索过程.下面我们介绍正五边形的一种尺规作图方法：

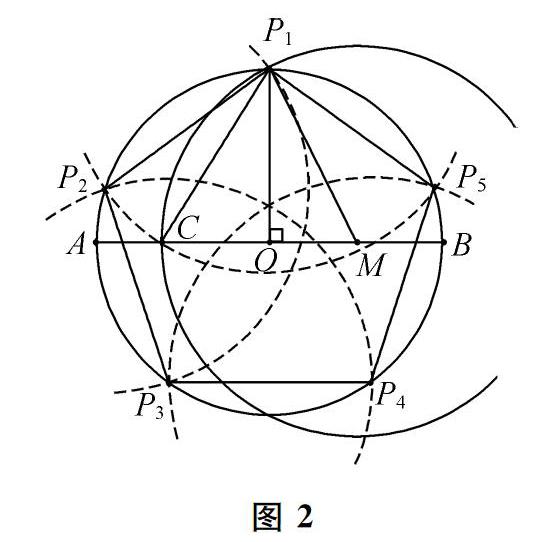
（l）设○是待作的正五边形的中心，P，是一个顶点，以○为 圆心、○P1为半径作网，它就是正五边形的外接圆，作直径AB垂直OP₁：

（2）以OB的中点M为圆心，MP₁为半径作圆，交OA于C点;

（3）以P₁为同心，CP₁为半径作圆，交外接圆于点P₂，P₅，它们就是正五边形的另两个顶点.

（4）以P₂为同心作同半径的圆，交外接网于另一点P₃，再以P₃。为圆心作同半径的圆，交外接圆于另一点P₄₁，顺次连结P₁P₂P₃P₄P₅，即得正五边形.

历史上，用尺规作图作正偶数边形如2ⁿ，3×2ⁿ，5×2ⁿ等正多边形并非难事，但对边数为奇数如7，9，11，13，15等的正多边形作图，在当时是件困难的事，而且并非都可以作图成功.

直到1796年，当时还是年仅19岁的大学二年级的高斯证明了正十七边形是可以用直尺和圆规作出的，这一发现震惊了当时的数学界，后来在1825年由费马给出并证明了正奇数边形的边数只有是费马素数或不同的费马素数乘积才可以尺规作图（费马素数是指形如F（n） =2²ⁿ+1的素数，其中n为非负整数）.

根据这个结论，对于我们早已掌握具体作图的正三边形、正五边形，现在还知道了它们为什么能用尺规作图，就因为3和5都是费马素数（3=F（0），5=F（1））;对于很久以来未找到办法来作出的正七边形，乃至于正十一边形、正十三边形，现在我们能有把握地说，它们不可能通过尺规作图作出，因为7，11，13都不是费马素数.

下面来点难度高的，对于正n边形，n=257，65537時，即使我们不知道具体如何作图，从理论上我们已经知道它们是可尺规作图的！

正多边形是美妙的图形，正多边形的尺规作图蕴含了丰富的数学知识，同学们不妨多多发挥自己的聪明才智，在几何图形的“精彩世界”里尽情遨游！