探究“雪花”曲线

张志勇

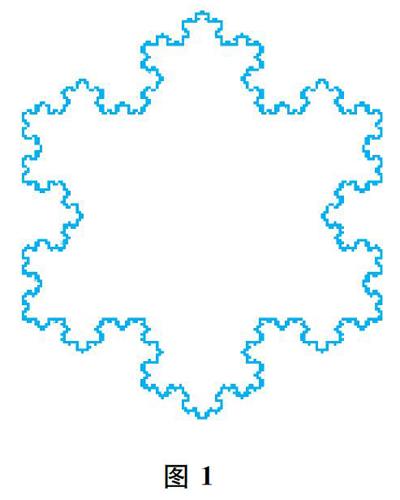
美丽的分形是大自然景物的抽象，它无比丰富的细节、绚丽多彩的结构常令我们流连忘返，图1中的科赫（Koch）雪花曲线等给我们以美的遐想.分形在多个领域有着广泛的应用，如物理中的湍流、化学中的高分子链、天文学中的星团分布、地理学中的河流与水系、生物学中的全息现象……

下面我们要探究的是美丽的分形背后的数学身影.

首先，我们来了解一点分形的科普小知识.提及分形，首先要涉及的是其自相似性，所谓自相似性即是指局部是整体成比例缩小的性质.通俗一点，就是当用不同倍数的照相机拍摄研究对象时，无论放大倍数如何改变，看到的照片都是相似的.由此，你能想象Koch雪花曲线的自相似性吗？

雪花曲线由瑞典数学家科赫于1904年构造，因为酷似雪花，所以叫“雪花曲线”.其构造规律是这样的：从图2-1所示的等边三角形开始（称为初始元），将三角形的每条边三等分，并在每条边三分后的中段向外作新的等边三角形（舍去中间的一段，保留两侧的两段，将中间的一段改成夹角为60。的两个等长的直线段，如图2—2），再细分便得到图2 - 3……不断重复这样的过程，隐去不要的部分，便可得到图1所示的雪花曲线.

从图形的构造过程不难理解雪花曲线的自相似性.其實在我们的教材必修《数学5》数列单元习题中，就有雪花曲线的构造.

雪花曲线的奥妙不仅在于它的自相似性，我们作出初始三角形的外接圆（如图3），可以发现雪花曲线永远不会超出这个圆，也就是说雪花曲线围成的面积是有限的，如果再告诉你，雪花曲线的周长却是无限长的，也就是说用一个无限长的图形围成一个有限的面积，是不是有点“难以置信”！

下面，我们用数列知识来证明这个结论，

我们设初始三角形ABC的边长为a，经过n次生长后，得到的小三角形的边长为a_n=

a（1/3）ⁿ，边数E_n=3·4ⁿ，面积为s_n=a²（1/3）²ⁿ，这样n次生长后总的周长之和为C_n=

a_nE_n=一3a（4/3）ⁿ，而所围成的面积之和s_n=a²（1/9）ⁿ·[8/5·9ⁿ-3/5·4ⁿ]=

a²[8/5-3/5（4/9）ⁿ]，这样生长无限次后，边长和即周长趋于无穷，而面积和则趋于定值

当然，要说明的是，这个令人惊异的结论，面积的有限性，要用到一丁点儿极限的知

识，但是我们可以这样想，在一张纸上画雪花曲线，不管生长多少次，它都不会超过一张纸

的，显然它的面积是有限的，

最后我还想告诉同学们的是，雪花曲线的神奇之处不仅如此.其身上还有很多不为人知的奥妙之处，如曲线上有许多折点，到处都是“尖端”;曲线虽然连续，但雪花曲线没有切线.

透过雪花曲线，我们可以深刻感受到：分形几何，不愧为“真正描述大自然的几何学”，它如此贴近我们的生活，不仅有外在之美，其内在深奥的数学之美更需要我们用数学的眼光去积极探索，随着我们学习的深入，或许会揭开其中更多的神秘面纱.