复杂框架结构工业厂房的静力弹塑性分析

李其成，徐敏，谢汝强，徐彬，沈小璞，

(1.安徽省工业工程设计院，安徽 合肥 230001；2.安徽建筑大学 土木工程学院，安徽 合肥 230031；3.建筑结构安徽省普通高校重点实验室，安徽 合肥 230001)

0 引言

地震灾害发生突然，破坏惨重，在时间、空间上具有不可预见性。为减少地震灾害造成的损失，耗能减震技术也在飞快发展。防屈曲支撑是一种良好的耗能装置，能够很好地耗散地震荷载下结构承受的静力及动力作用能量，提高其吸能耗能能力。Kimura[1]等人在1976年第一个提出了钢管内填砂浆来约束的防屈曲支撑，并做了滞回性能试验。霍雨佳[2]研究了三维钢筋混凝土高层框架结构Pushover分析方法的保证率。马来飞[3]针对宁德师范学院体育馆结构分别使用PKPM、MIDAS以及SAP2000软件对其进行计算分析，并进行了各软件计算结果的对比。本文基于SAP2000有限元分析软件平台，对某多层复杂框架结构进行模态分析、反应谱分析两种线性分析，同时进行了一种非线性静力弹塑性分析，即推覆分析方法(Pushover)。通过多种工况类型的静力弹塑性分析，得到了原结构和增设耗能装置结构的自振周期、层间位移角、顶点位移及塑性铰分布情况。通过对比原框架结构模型(一)和布置耗能装置框架结构模型(二)分析结果，得到了复杂工业厂房加设防屈曲支撑后，可有效提高结构的抗震性能等实用性结论。

1 工程概况

合肥市某垃圾处理厂车间建筑面积2790 m2，建筑总高度21.95 m，占地面积1142 m2，结构型式为八层(包括夹层)框架结构。楼板开洞率大，设备运行重量最大达300 t。分别在4.5 m、7.5 m标高处设有夹层；在标高14.2 m处设有人员操作走道；标高17.7 m处设有2台10 t的行车。车间柱网主要是10 m×10 m和12 m×12 m。为了研究防屈曲支撑在框架结构中是否起到良好的耗能作用，分别建立未加支撑的原结构模型和加设防屈曲支撑的耗能结构模型。并采用SAP2000有限元软件进行数值模拟分析，各层层高详见表1所示。

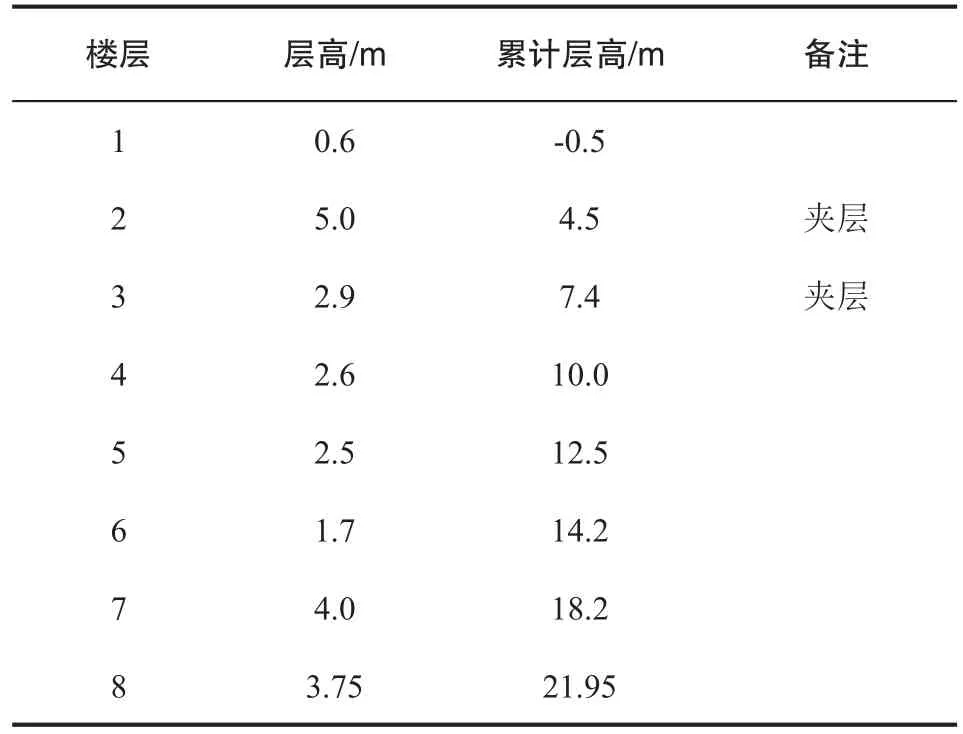
表1 结构层高

框架梁柱均采用C30混凝土，主筋采用HRB400，箍筋为HPB300；楼板厚度120 mm，框架柱截面尺寸分别为800 mm×800 mm和800 mm×600 mm两种，框架梁截面主要有250 mm×800 mm、400 mm×800 mm 和 350 mm×1000 mm三种。工程设计使用年限为50年，建筑抗震设防烈度为7度，设计基本地震加速度为0.10 g，设防地震分组为第二组，场地类别为Ⅱ类，特征周期为0.40 s。整个车间特点是层高大；柱网较大；设备运行重；有穿层柱；开洞率大，如第四层开有洞大，占整个楼层面积约40%，楼板缺失较多，结构刚度不均匀。

2 支撑构造及布置情况

模型(二)所采用的防屈曲支撑是一种新型耗能材料，由内芯、外围约束机制以及两者中间的无粘结材料三部分组成，无粘结材料通常采用硅胶，防屈曲支撑参数根据《建筑消能减震技术规程》[4]选取，如表2所示。支撑布置见图1-图8所示(红色虚线处为支撑所在位置)。

表2 防屈曲支撑参数

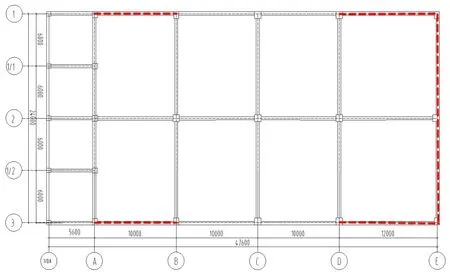
图1 标高‐0.5 m处支撑布置

图2 标高4.5 m处支撑布置

图3 标高10 m处支撑布置

图4 标高14.2 m处支撑布置

图5 标高18.2 m处支撑布置

图6 A轴线支撑布置

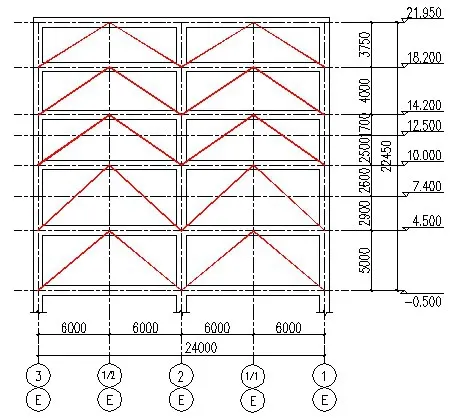
图7 E轴线支撑布置

图8 1、3轴线支撑布置

3 抗震性能分析

3.1 模态分析

模态分析给反应谱分析和时程分析提供分析的基础。而防屈曲支撑正是通过对框架结构动力特性的影响来提高结构的抗震性能。Ritz向量法可以避免高阶振型截取带来的误差，能获得更精确的计算结果[5]，则采用Ritz向量法进行模态解耦，得出结构前12阶的质量参与系数和自振周期，详见表3和表4所示。小于0.9，不满足基本振型下所需要达到的质量参与系数下限的要求。而加设支撑耗能结构后，即模型(二)的质量参与系数得到了较大提高，在X、Y方向各振型质量参与系数的累加值均大于0.9，满足“抗震设计规范”(以下简称“抗规”)[6]所需要达到的累计质量下限的要求。模型(二)的自振周期小于模型(一)，说明加设支撑耗能结构后的框架结构刚度增大。对比分析RZ与UX+UY的数值，可以看出模型(一)和模型(二)的第一振型、第二振型均分别以X向和Y向的平动为主的，而两者模型的第三振型均以结构的扭转振型为主[7]。模型(一)和模型(二)的第三振型与第一振型的比值分别为Tt/T1=0.6769和 Tt/T1=0.6823均小于 0.9，低于“抗规”中规定的结构扭转响应上限，降低了结构扭转效应潜在的破坏力，是满足抗震规范要求的。

表3 模型(一)的自振周期与质量参与系数

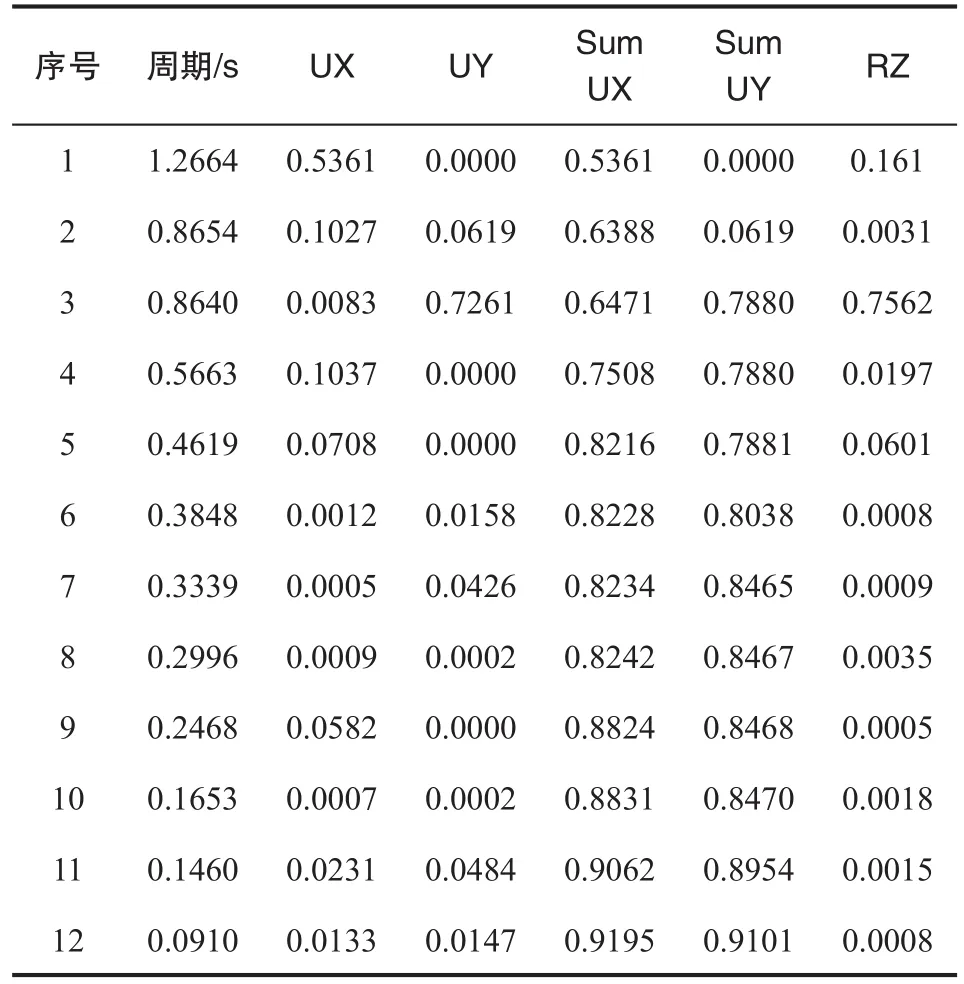
表4 模型(二)的自振周期与质量参与系数

3.2 振型分解反应谱法分析

振型分解反应谱法分析是一种拟动力分析方法，使用动力方法计算质点地震响应，再使用统计的方法形成反应谱曲线，本文根据合肥地区实际情况选取反应谱曲线，最后采用静力方法进行结构分析[8]。层间水平位移角是多遇地震作用标准值产生的层间最大弹性位移与层高的比值[9]。振型分解反应谱法分析得出的顶点位移与最大层间位移角计算结果详见表5所示。

表5 结构顶点位移和层间位移角

由表5中结果对比可知，加设防屈曲支撑后，顶点位移从50.81 mm降至19.9 mm，减少了60.83%。可见设置耗能构件可有效提高结构的变形能力，以此吸收和消耗地震能量。模型(一)最大层间位移角为1/305，大于“抗规”规定的层间位移角限制1/550。因此，在多遇地震作用下进入弹塑性阶段，模型(一)结构不满足规范规定。模型(二)结构最大层间位移角为1/724，是满足“抗规”规定的，结构能够保持弹性阶段工作，不受损坏[10]。两者最大层间位移角均出现在第二层，可知薄弱环节在是在第二楼层。

4 静力弹塑性分析

为了进一步分析在大震作用下两个模型结构出现弹塑性破坏的形态，采用了静力弹塑性分析方法。按一定的水平荷载加载方式，对结构施加单调递增的水平荷载，并逐步将结构推覆至预定的目标位移，分析结构的非线性性能，判别结构及构件的受力及变形是否满足设计要求[11]。文中截取单榀框架以便观察塑性铰分布情况，以此分析结构变形及抗震性能。

4.1 性能点分析

文中采用由位移控制进行加载控制，依据定义大震作用下的反应谱函数[12]。建筑的抗震设防烈度为7度，在大震作用下，水平地震影响系数最大值αmax=0.5，周期折减系数为0.8，阻尼比取0.05。在罕遇地震作用下能力谱曲线见图9-图10所示，性能点参数具体参见表6。

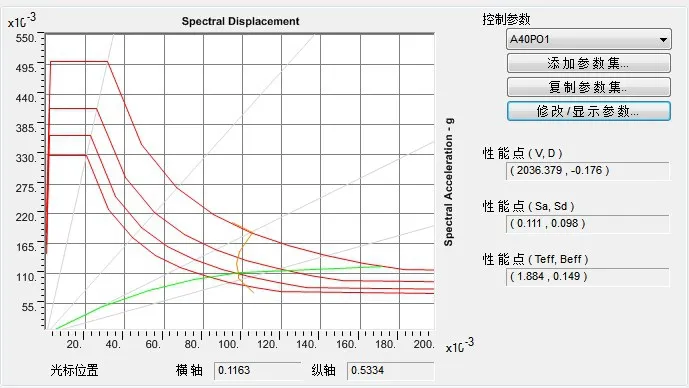
图9 模型(一)能力谱曲线

图10 模型(二)能力谱曲线

表6 性能点参数

从表6可知，在罕遇地震作用下，模型(二)的基底剪力远大于模型(一)，增大63.74%；而顶点位移相对模型(一)减少了91.48%；最大层间位移角相对模型(一)减少了82.36%，两模型都位于结构第二层。分析中可以看到模型(二)的抗侧移刚度更大、变形能力更强[13]。在从图10中可以看出，模型(二)能力谱曲线过早的穿出需求谱曲线，表明模型(二)能够抵抗大震下的地震作用，且仍然处于弹性阶段，满足抗震设防需求。

4.2 塑性铰分析

从表7～表8中可以看出，框架结构的塑性铰发展变化，对照表6中性能点的基底剪力以及顶点位移数值，分别找出模型(一)在大震作用下其性能点[14]位于第21步，模型(二)的性能点位于第24步。模型(一)在39步后的基底剪力基本保持不变，顶点位移减小，模型(二)在41步后的基底剪力基本保持不变，顶点位移减小，显示模型被推坏。各模型罕遇地震下框架结构达到极限破坏时的塑性铰分布情况见图11～图18所示。

表7 模型(一)塑性铰发展情况

图11 模型(一)A轴线塑性铰分布图

图13 模型(一)E轴线塑性铰分布图

图15 模型(一)1轴线塑性铰分布图

图17 模型(一)3轴线塑性铰分布图

图12 模型(二)A轴线塑性铰分布图

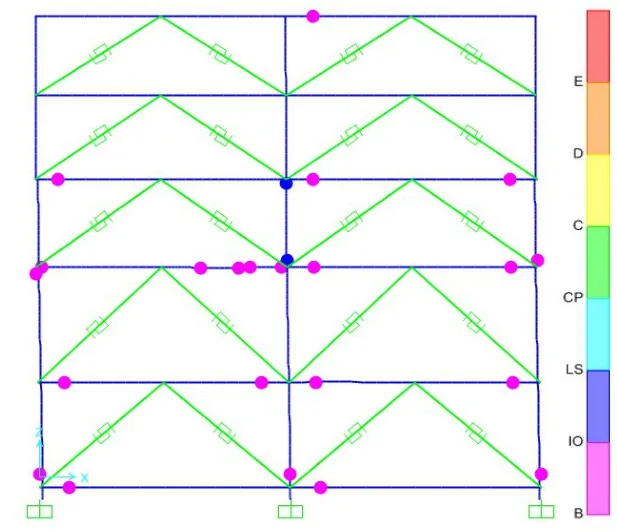
图14 模型(二)E轴线塑性铰分布图

图16 模型(二)1轴线塑性铰分布图

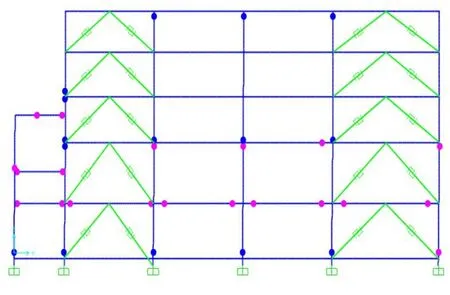
图18 模型(二)3轴线塑性铰分布图

两模型均在主梁起始端相对距离的0.1与0.9处设置了M3型塑性铰，柱起始端相对距离0.1与0.9处设置了PMM型塑性铰。柱有128根，梁有217根，因此共设置塑性铰690个。当达到极限破坏状态时，模型(一)出现了超过极限承载力的塑性铰，位于第二层。其中B-IO阶段塑性铰共148个，柱上有45个，梁上有103个。在IO-LS阶段中塑性铰共66个，其中在柱上出现21个，梁上出现45个。到达C-D阶段时，共有45个铰，柱上26个塑性铰，梁上19个铰，使得原结构在大震下发生破坏。在D到E阶段有14个铰，都出现在框架梁上。在原结构上增设防屈曲支撑后，在极限破坏状态时，模型(二)在B-IO阶段塑性铰共出现137个，有16个在柱上，其余121个出现在梁上。IO-LS阶段塑性铰共有105个，有4个出现在柱上，其余101个出现在梁上。在达到C-D阶段时，共出现了23个塑性铰，其中15个在梁上，8个在柱上，说明加上防屈曲支撑后，抗侧移刚度增大，显示出加设防屈曲支撑后的结构抗震性能有较大提升，且变形能力更强，达到在大震下作用下不倒塌的目的。由上述统计数据分析，结构在增设支撑后的抗侧移刚度增大，塑性铰较多的出现在框架梁上，充分体现出“强柱弱梁”的设计理念要求。从表6可以看出，原结构最大层间位移角为1/11，出现在结构第二层，不符合“抗规”中规定最大弹塑性层间位移角限值1/50要求，而加设耗能支撑构件后，结构最大层间位移角为1/63，满足抗震规范要求。

5 结论

文中结合实际工程，并针对两种不同结构模型利用模态、反应谱和静力弹塑性(Pushover)等方法进行抗震性能分析。所获得结果显示设置防屈曲支撑可以大幅提高抗侧移刚度和变形能力等性能指标，并显著提高结构的抗震性能。综上所述，得出以下几点结论：

(1)对比振型分解反应谱法以及Pushover法分析结果，发现结构和最大层间位移角都出现在第二层。

(2)在原结构分析过程中，最大层间位移角不满足“抗规”中的最大层间位移角限值；而在设置防屈曲支撑后，结构最大层间位移角符合“抗规”要求。由此可见，结构因刚度不足过早丧失结构承载力时，可设置防屈曲支撑增加结构的抗震赘余度，并能够在多遇地震作用下，使得结构具有良好的耗能能力。

(3)从Pushover分析结果可见，未设置耗能构件的原结构塑性铰在大震作用下塑性情况发展严重，导致结构倒塌。而设置防屈曲支撑后结构基底剪力增加，顶点位移大幅减小，且塑性铰大部分都出现在梁上，符合“强柱弱梁”的抗震设计理念；此外，通过对比分析对结构的破坏机制进行了量化评估，为基于性能的抗震设计和评价提供较为精确和有效的途径。