基于拱肋合理成桥状态的扣索索力优化计算

赵砥，胡成，刘梦迪

(合肥工业大学 土木与水利工程学院，安徽 合肥 230009)

0 引言

通常上承式拱桥结构主要包括主拱、主梁、立柱等主要构件，而拱桥结构整体的合理成桥状态就是其主要的受力构件均达到其各自的合理内力状态。

拱肋在不同的荷载工况组合下，要保证其成桥内力状态合理，就要控制恒载弯矩在较小的范围，尽量使得拱肋截面处于均匀受压状态。拱肋作为一种将竖向力转化为水平推力的结构，只有当拱截面内力主要以受压为主才能充分发挥这一特点。而拱肋截面偏心距的大小直接反映了拱肋的内力状态，因此主拱在成桥状态下应该保证较小的截面偏心距[1-2]。

本文的索力优化研究主要是以扣挂法悬拼拱桥整体成桥时拱肋的内力状态作为其合理成桥状态的控制目标，并以此来建立拱肋悬拼合龙前的索力优化分析模型，并借助白水江特大桥实际工程进行数值有限元分析，以证明该优化方法的准确及有效。

1 工程背景

白水江特大桥主桥桥面系跨径布置为22×16=352 m，主拱跨径330 m，是一座上承式钢箱桁肋拱桥[3]。桥型布置见图1所示。

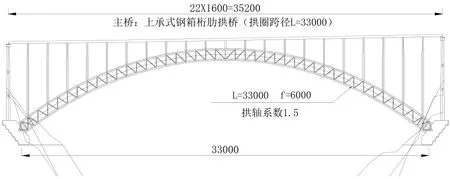
图1 主桥桥型布置图(单位：cm)

主桥拱肋为钢桁架结构，上、下弦杆为小钢箱截面，拱肋在横桥向分为三片，为等高桁架，桁高(上、下弦中心线间距)8.5 m，拱肋钢箱断面内轮廓尺寸为1.4 m×1.0 m，内部设有纵向加劲肋，钢桁拱肋上、下弦杆钢箱壁厚从拱顶至拱脚分节段变厚。

拱上立柱为三柱式钢箱桁架柱，立柱纵桥向间距为16 m，立柱截面为等截面钢箱，钢箱截面横桥向尺寸为1.0 m，顺桥向尺寸为1.6～1.26 m，内部设有加劲肋与横隔板。当立柱高大于12 m时柱间设置交叉斜撑，立柱顶与刚格构主纵梁焊接。

主跨桥面系钢梁采用钢混叠合梁，钢格构主梁主要由纵梁、次纵梁、横梁构成，横梁与纵梁之间采用栓焊结合的连接方式。

主桥拱肋依照排架立柱所处位置共划分为10对拱段和一个合龙段，均采用缆索吊装斜拉扣挂法施工。其悬拼总体布置图如图2所示。

2 非线性规划模型

2.1 概述

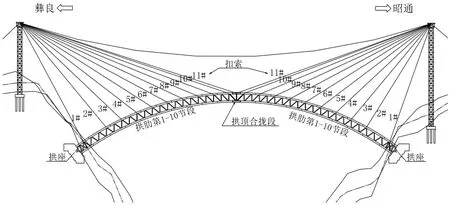
图2 悬拼总体布置图

非线性规划在做优化分析时，要明确工程实际中涉及的目标值、变量和约束条件三个因素，从而根据三者的关系建立起数学模型。非线性规划模型常见形式如式(1)表示[4]。

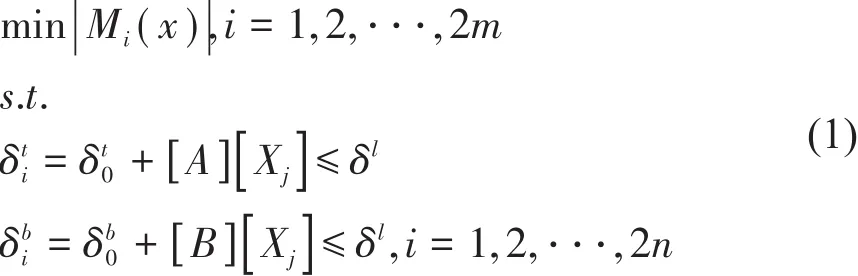
(1)设计变量

在建立优化模型时，需要根据实际工程选择特定的参数，其中用来改变自身数值来影响目标值改变的这组参数即为设计变量，设计变量常用X表示，在优化模型中一般用x1,x2,…,xn表示，构成向量X={x1,x2,…,xn}T。

(2)目标函数

目标函数要选择最能贴切反映研究对象目标状态的某一参数，而且目标函数与上述设计变量之间一定要有直接或间接的联系，目标函数常用minf(x1,x2,…,xi)表示。

(3)约束条件

约束条件可以使设计变量在一个相对合理且具有工程意义的范围内变化，起到限制的作用，约束条件常用gi(x1,x2,…,xn)=0和gj(x1,x2,…,xn)≥0来表示。

非线性规划的求解方法主要有罚函数法、障碍函数法等，本文主要借助Matlab软件编程进行目标函数的优化求解[5]。

2.2 悬拼拱桥合龙前索力调整优化模型

对于大跨径拱桥由于其拱肋节段数量较多，扣索索力调整的次数也随之增加，如果索力优化时仍然选择全部扣索进行索力调整将会继续增加施工工作量，也会降低施工安全性。因此本优化过程，只选择部分扣索进行索力调整，拱肋合龙前结构的计算简图如图3所示：

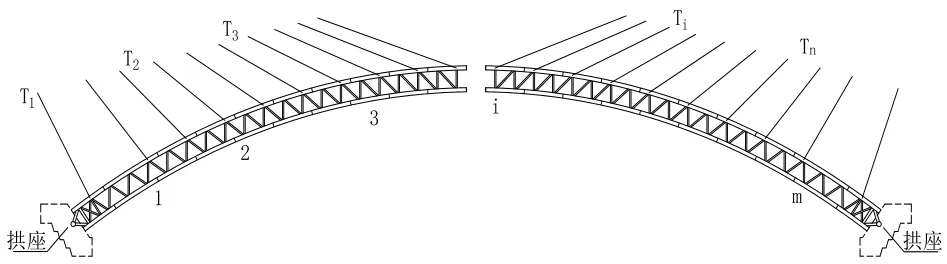
图3 拱肋合龙前结构计算简图

本优化模型选择的设计变量数目为n，即所选择的索力调整的扣索数目为n，设n根扣索的索力改变量分别为 Δx1,Δx2,…,Δxn，用向量 X 表示，形式如式(2)所示：

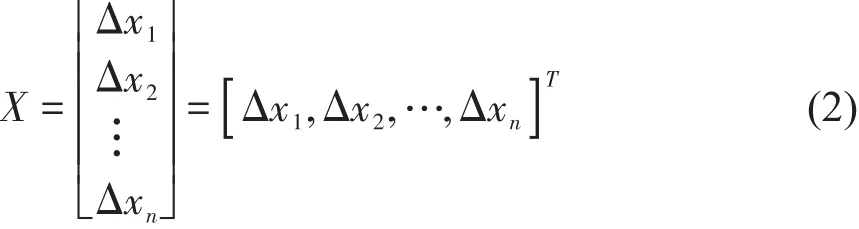
本模型以成桥后拱肋的内力状态作为控制目标，保证成桥后拱肋偏离弯矩较小以尽量使截面均匀受压。截面受压偏心距最能反映偏离弯矩的大小，因此以成桥后拱肋截面受压偏心距作为依据[6][7]。本文选取拱肋上m个截面作为偏心距控制截面，并求解其偏心距平方和的算数平方根。则目标函数如式(3)所示：

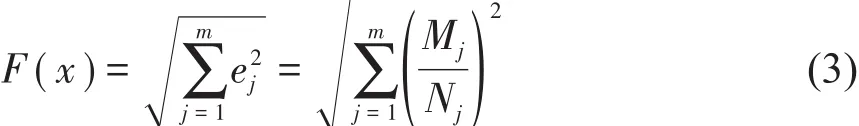
上式中，Mj表示为索力调整后的成桥拱肋的偏心距控制截面j的弯矩值，Nj表示为索力调整后的成桥拱肋的偏心距控制截面j的轴力值。

通过计算分析设计变量改变对目标函数的影响，可以得到目标函数与设计变量之间的关系。

选取未进行索力优化状态下成桥拱肋的最大应力截面作为应力控制截面，假设该截面为p个，选取其截面应力为约束条件。

2.3 优化模型求解过程

(1)合龙前大悬臂状态下不进行索力调整，得到成桥时拱肋偏心距控制截面的弯矩值M0j、轴力值N；再计算提取应力控制截面的上缘应力0j及下缘应力

(2)将设计变量中的相关扣索改变单位力，得到成桥后拱肋偏心距控制截面的弯矩影响矩阵A和轴力影响矩阵B，应力控制截面上缘应力影响矩阵C和下缘应力影响矩阵D；

(3)由上述过程得到成桥状态下拱肋偏心距控制截面的弯矩及轴力表达式；再计算目标函数偏心距平方和的算数平方根以及约束条件中截面上、下缘应力表达式；

(4)通过Matlab软件，结合求得的目标函数以及约束条件表达式，建立针对非线性规划问题的数学模型。

2.4 Matlab求解流程编制

Matlab中有很多适用于解决不同目标函数的已编译程序可以进行直接调用，如求解非线性规划问题中的最小值求解程序fmincon函数[8]。

可直接调用上述优化函数fmincon，建立白水江特大桥合龙前索力调整求解主程序，具体可见文献[3]。

2.5 计算要点

(1)由于白水江特大桥拱肋是由上、下箱形截面弦杆和竖向腹杆拼接的桁架结构，因此控制截面的弯矩值M和轴力值N以及其改变量，可由该处上、下弦杆(箱形截面)弯矩值和轴力值及其改变量的平均值来代替，而上缘应力即取值上弦杆顶板应力，下缘应力即取值下弦杆底板应力。

(2)为了避免实际张拉时扣索张拉次数过多，只选择空间上分布较远的几根扣索作为设计变量，以减小扣索之间的互相影响。白水江特大桥合龙前的索力优化调整选取两岸3号、6号、10号共6根扣索进行局部索力调整分析。

(3)白水江特大桥拱肋偏心距控制截面为9个，即彝良岸拱脚截面、L/8截面、L/4截面、3L/8截面、L/2截面、5L/8截面、3L/4截面、7L/8截面、昭通岸拱脚截面。

(4)选取成桥后拱顶截面上缘和拱肋L/4截面下缘作为应力控制截面，并将这两处截面应力作为优化模型的约束条件。

(5)fmincon函数的初始设计变量值可取x0=()10,10,10,10,10,10，即6根索力值可从10 kN开始迭代，为保证索力调整时拱肋线形不至于发生过大变化，索力改变量下限值取-300 kN，上限值取+300 kN(计算影响矩阵时单位力取1 kN)。

2.6 优化模型计算

将上述规划模型参数代入到Matlab优化程序中，经过了69步迭代之后输出了目标函数最优值和对应的设计变量值。迭代过程及计算结果如图4所示。

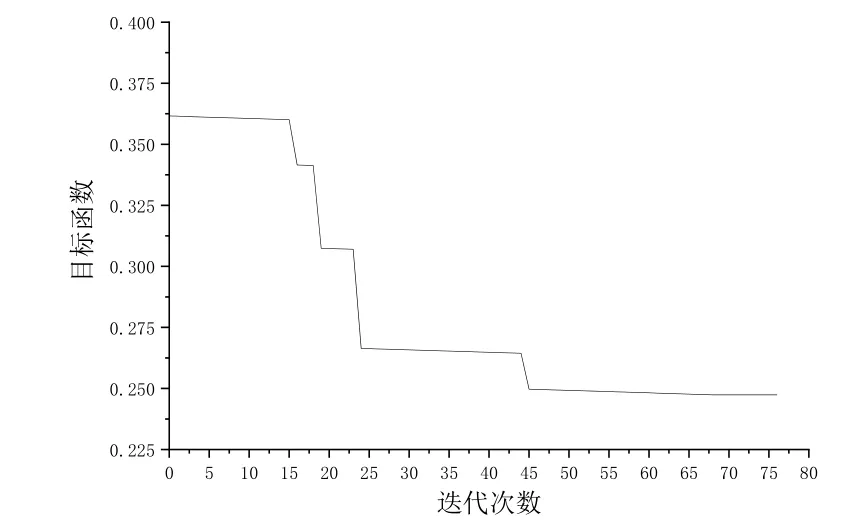
图4 目标函数迭代过程图

白水江特大桥目标函数在数学模型优化前后目标函数值如表1所示。

表1 数学模型目标函数优化前后对比

如表1所示，未优化状态下的目标函数为0.3616，优化之后目标函数变为0.2474，优化比例达到31.58%，说明拱肋偏心距控制截面的偏心距整体减小，拱肋均匀受压性能有所改善。

3 有限元法验证

为证明上述优化方法的准确性，进一步使用Midas Civil软件进行全桥建模计算，如图5所示。

在本算例全桥有限元模型中选择梁单元建立模型，全桥共2717个单元，1433个节点。

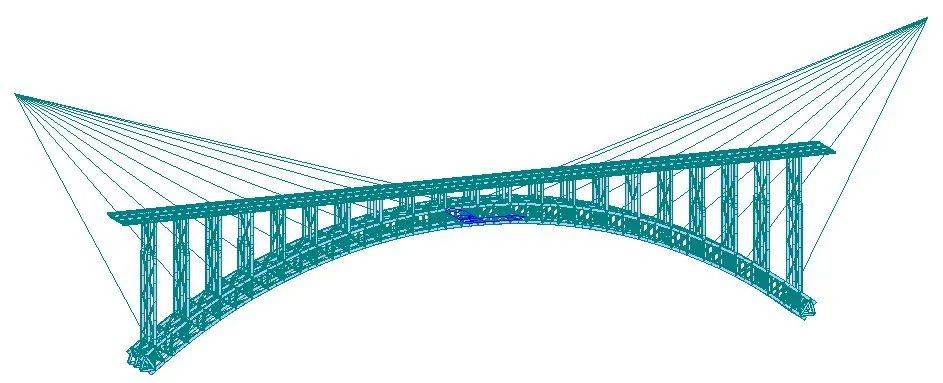
图5 Midas Civil全桥模型示意图

3.1 目标函数优化结果

通过上述Matlab程序计算后输出得到的设计变量值：x1=196.46 kN，x2=272.91 kN，x3=-164.88 kN，x4=-170.86 kN，x5=282.41 kN，x6=192.44 kN，将所得的这6根扣索的索力调整值代入有限元模型中计算，得到成桥后拱肋偏心距控制截面的内力和弯矩，并计算目标函数值。目标函数值优化前后如表2所示。

表2 正装模拟目标函数值优化前后对比

分析表明，初始迭代值为0.3616，优化后目标函数减小为0.2512，优化比例达到30.53%。与表1相比两表中得到的目标函数值不同，是因为在计算轴力、弯矩影响矩阵的时候是逐根张拉扣索进行求解得到的，即不考虑设计变量之间的互相影响，这与实际张拉情况并不完全一致，因此将得到的索力调整值代入有限元模型计算得到的目标函数与优化模型得到的结果有所差异。但对比可知，该差异值较小，因此利用该数学模型进行优化计算是准确的。

3.2 成桥后拱肋内力优化

优化前后的成桥拱肋内力结果如表3及图6所示(图中横坐标1～64表示从彝良岸至昭通岸各控制截面)。

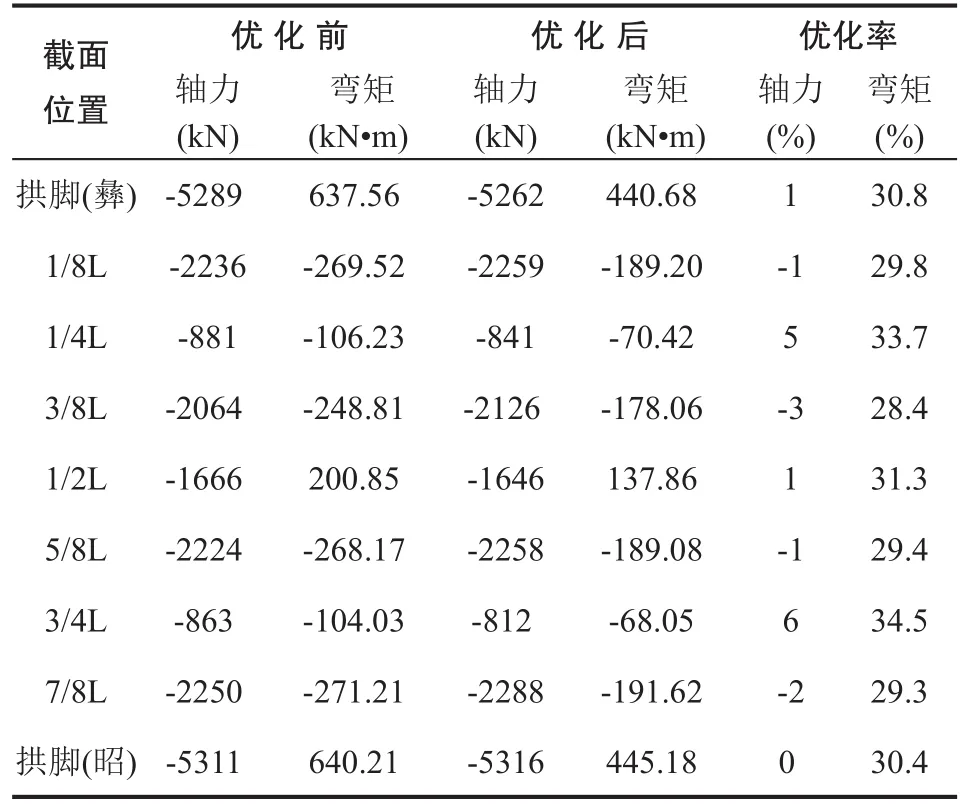
表3 恒载作用下控制截面内力优化前后对比

由表3可看出，虽然索力优化后对拱肋轴力的影响值较小，但是各截面弯矩绝对值均得到有效减小，优化幅度达28%以上。

优化前后的成桥拱肋弯矩对比如图6所示。优化前拱脚处的弯矩较大，优化后两岸拱脚截面的弯矩得到有效控制，偏心距较大的L/4处拱肋截面弯矩也得到了大为减低，表明拱肋合龙前选择较少数目的扣索进行调整即可达到优化拱肋成桥内力的作用。

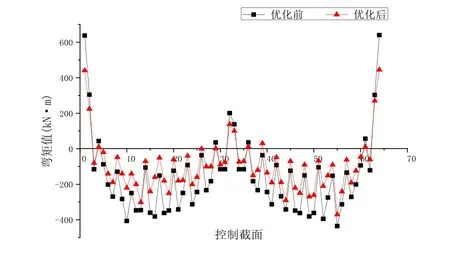
图6 Midas Civil全桥弯矩分布图

优化前后的成桥拱肋截面上、下缘应力变化分别如图7、图8所示，图中横坐标1～64表示从彝良岸至昭通岸各控制截面。

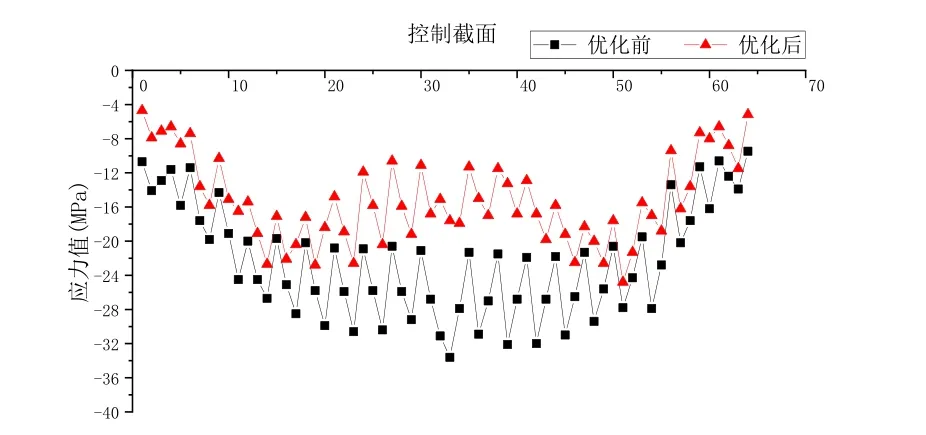
图7 拱肋截面上缘应力优化前后对比图

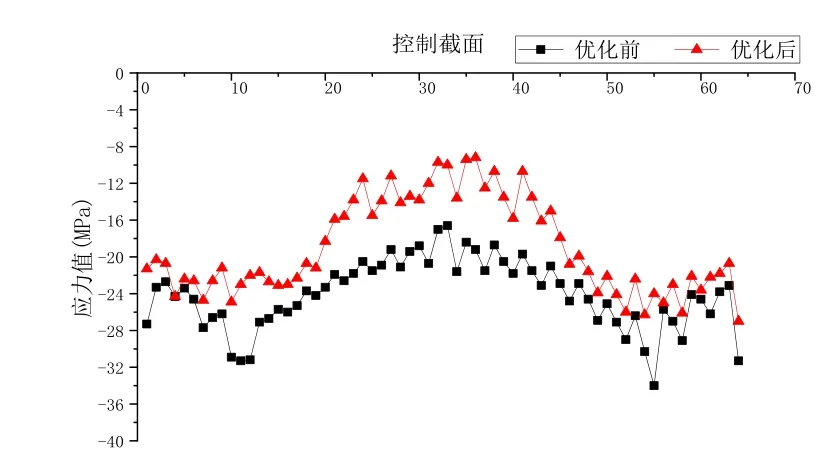
图8 拱肋截面下缘应力优化前后对比图

分析可知，合龙前进行局部扣索索力优化调整后，成桥时拱肋截面上缘最大压应力为-24.8 MPa(小于优化前-33.59 MPa)，拱肋截面下缘最大压应力为-27.0 MPa(小于优化前-34.0 MPa)，拱肋截面上、下缘应力均有所降低。

4 结论

本文以实现白水江特大桥合理成桥状态所进行的合龙前的扣索索力优化为研究对象，阐述了利用非线性规划和Matlab来解决优化问题的具体分析过程，并结合此工程项目进行计算分析，得出以下结论：

(1)扣挂法拱桥悬拼施工的索力优化调整在编制优化模型的求解程序时可直接调用Matlab软件中提供的已编译函数fmincon，计算结果可行。

(2)以成桥后拱肋偏心距控制截面的偏心距平方和的算数平方根作为目标函数构建的合龙前索力优化的非线性规划模型符合实现拱肋合理成桥状态的要求。

(3)有限元计算及分析对比表明，本文的索力优化模型是合理可行的。通过局部的索力优化即可使拱肋成桥内力状态得到了较好的改善，拱肋截面更接近均匀受压，同时截面弯矩值降低幅度可达28%以上。