基于影响矩阵法的钢斜拉桥二次调索

严 松，王 耿

（中交第二公路勘察设计研究院有限公司，湖北 武汉430052）

1 概述

密索体系的整体式扁平钢箱梁斜拉桥不仅具有传统斜拉桥塔、梁、索合理协同受力的特点，还因自重轻、抗扭和横向抗弯刚度大且便于工厂化生产等优点正成为现代城市桥梁发展中的翘楚，可满足景观需求。

钢箱梁斜拉桥施工过程中大多伴有结构体系变化和结构荷载随工序增加的特点。施工监控和及时纠偏是直接影响成桥状态结构力学性能的与设计要求符合性的关键因素[1]。鉴于斜拉桥施工工序的复杂性以及各类施工综合不利因素的影响，成桥阶段主梁线形或索力状态与设计理想状态存在误差，需进行二次调索以进行误差调整。国内大多数斜拉桥施工中尽量保证线形并兼顾结构内力不超限，而在成桥后通过索力调整结构内力状态[2]。

影响矩阵法已广泛应用于斜拉桥和系杆拱桥的二次调索计算，其实用性已被许多工程实践所验证。斜拉桥成桥阶段二次调索的索力调整量相较于被调前的索力小得多，且被调前的结构布置和内力状态确定，运用线性假定结合单位荷载法并通过有限元模型计算可提取调整前结构的影响矩阵。选定不同的被调参数得到的影响矩阵的含义有所不同，调整参数与被调参数的相对大小也直接关系到方程组的求解方法。文章以国内某双塔单索面钢箱梁斜拉桥为工程背景，提出基于关心截面处索力调整的影响矩阵法，对成桥阶段索力进行二次索力调整以满足工程设计要求。

2 影响矩阵法

2.1 索力调整的矩阵表达式

二次调索前选取作为控制变量的某些关心截面上n个独立结构特性参数所组集的列向量称为调值向量{E}，其中的单个元素可指定为内力调整量或位移调整量。结构中被调截面上指定调整以引起调值向量发生变化的m个独立未知量所组集的列向量称为被调向量{x}，其中的单个元素为被调截面的内力或位移。影响矩阵[A]中（m×n阵）元素aij表示被调向量中的第j个元素发生单位变化引起调值向量中的第i个元素的变化量，见式(1)。二次调索的初始索力{T0}为成桥阶段由频率法原理实测的索力，二次调索后的目标索力{T}为设计索力。对于索力调整计算而言，我们关注的是截面位移以及索力变化量，将[A]矩阵关于关心截面处的位移元素依次置于末行，则{T}-{T0}对应于调值向量{E}中除位移行的索力调值向量部分。

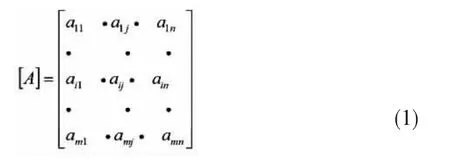
在前述线性假定条件下，根据线性叠加原理，索力调整方程组的矩阵形式可写为：

成桥阶段索力计算调整时，被调向量个数m一般大于调值向量个数n，仅凭(2)式不能得到被调向量的唯一解。需提出索力优化的目标函数，采用优化算法求解对应目标函数的被调向量，即最优的索力调整向量。后文中将论述成桥阶段以索力控制为主，标高控制为辅进行成桥阶段误差调整的方法，此时[A]矩阵中只包含关心截面处的索力元素，仅凭(2)式则可得到被调向量的唯一解。实际调索计算中通过有限元软件结合Matlab可十分方便地进行索力调整计算。

2.2 影响矩阵的提取

二次调索阶段结构存在初始索力，张拉任一根索对其余索的索力均有影响，主梁关心截面上的标高也会相应变化。如图（1）b所示，i索两端施以单位力P=1后，索内内力变化为 ΔF，图（1）c中 i索端实际外力P=1-ΔF，故由图（1）b所求得的控制点调值向量除以1-ΔF即可得到影响矩阵中第j列的向量。需要注意的是，根据拟定的合理调索顺序对斜拉索逐根张拉得到的影响向量中包含了关心截面对应位置处位移变化量的元素，一般将其写在向量的末端。则需控制位移变化量的关心截面数量即为m-n个。

图1 影响向量计算示意图

而对于成桥索力调整计算而言，特别对于塔梁墩固结体系的斜拉桥而言，若成桥后靠近主塔附近梁段的整体标高与设计有较大差距时，成桥阶段对于索力的调整难以使成桥线形准确达到设计线形，而主要以成桥索力控制为主，避免因过度调整标高造成局部梁段应力超限或冗余度过小，影响运营期主梁安全。

2.3 施调向量{TS}的计算

成桥阶段二次调索前、调索后的设计索力列向量为{T0}、{T}，索力施调向量为{TS}，不含位移元素的索力影响矩阵为[A]，则索力调整计算式写为：

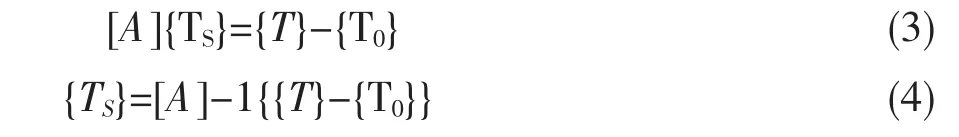
实际施工监控中对成桥索力的调整计算需要建立准确的有限元模型，通过索力施调向量的不断迭代计算，最终得到一组满足索力误差要求的成桥索力，而不可能与设计成桥索力完全一致。同时，根据局部调索过程中现场实测索力变化与理论计算值的差值，可实时调整模型中下一批索力施调量，在不断的实测与理论计算对比调整过程中通过一次索力调整到达全桥索力调整的目标。施调向量{TS}的具体计算过程如下。

二期恒载下，计算模型中以拟定的最佳调索顺序，根据影响矩阵法原理逐一施工阶段对拉索施加固定力值的拉力，并逐一提取每阶段全桥索力的变化量，对所有索力张拉施工阶段的索力增量结果进行归一化处理后即可得到索力影响矩阵[A]。

根据索力影响矩阵[A]和式(4)，通过影响矩阵法和Matlab矩阵运算求出一次施调向量{TS1}，得到的成桥索力向量{T1}与成桥设计索力向量{T}作差后再次代入式(4)，计算出增调向量{FS1}，则有：

从而模型中二次迭代计算的施调向量 {TS2}可写为：

Midas模型计算时，用施调量{TS2}替代{TS1}，即以原来调索顺序将每个调索施工阶段中的索力值换成{TS2}向量对应的索力值重新运行计算，得到的成桥索力向量{T2}，可以发现{T2}更加接近于成桥设计索力向量{T}。同理，以索力向量的差{T2}-{T}再次代入式(4)，计算出增调向量{TS2}，依次类推迭代若干次后，{Tn}-{T}逐渐减小，当满足设计要求的误差限值时，则最后一次迭代计算得到的施调量{Tn}即可作为施调向量{TS}。

3 工程应用

某双塔单索面钢箱梁斜拉桥跨径布置为50+96+192+70＝408m，中心梁高3.0m，箱梁顶板宽29.5m，结构总体布置如图2所示。

图2 结构总体布置图

3.1 全桥有限元模型的建立

采用MIDAS/CIVIL桥梁计算软件建立有限元模型，梁单元模拟塔、梁和墩构件，只受拉桁架单元模拟全桥28对拉索，拉索、索塔与主梁节点之间均采用刚性连接。有限元模型如图3所示。

图3 有限元模型

3.2 提取索力影响矩阵[A]

成桥阶段索力二次调整张拉过程中，遵循近塔端至远塔端对称张拉的原则，拟定设计张拉顺序为 ：B1.Z1/B14.Z14→B2.Z2/B13.Z13→B3.Z3/B12.Z12→B4.Z4/B11.Z11→B5.Z5/B10.Z10→B6.Z6→B7.Z7→B8.Z8→B9.Z9。在Midas施工阶段中以此张拉顺序单独设置每对拉索施加单位力(10kN)为一个工况，逐工况叠加计算后再逆施工阶段提取索力值作差后即可整理出索力相关影响矩阵。限于全部矩阵较大，现只列出16组的索力影响矩阵见表1。

表1 16组（共28组）索力影响矩阵

3.3 计算施调向量{TS}

由以上单位荷载法结合有限元软件计算得到本例斜拉桥28阶索力影响矩阵，结合Matlab矩阵运算得到二次调索最终索力施调向量{TS}，即可由二次调索前全桥索力{T1}达到满足成桥设计索力{T}的精度要求的最终成桥索力{T3}，见表2，误差不超过10%。

表2 二次调索索力施调向量以及成桥索力

3.4 二次调索结果

由表2调索结果可知：通过本文拟定的二次调索顺序，结合索力影响矩阵法和有限元计算方法对成桥索力进行终调可在较少迭代次数条件下快速达到全桥索力的二次准确调整。索力调整前后对比如图4所示。

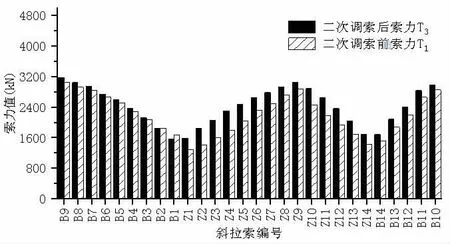
图4 索力优化前后对比

4 结论

文章斜拉桥索力监控的二次调索计算中，基于成桥索力误差调整阶段线性假定条件，采用单位荷载法求解索力优化的影响矩阵，并结合有限元模型计算得到遵循近塔端至远塔端对称张拉原则的索力施调向量，对全桥索力进行了准确的二次索力调整。

现场监控计算过程中通过有限次的有限元模型迭代计算便可快速达到设计索力的精度要求，成桥索力误差限在10%以内，表明本文提出的索力二次调整计算的方案能满足索力优化目标的基本要求，可作为施工监控的首选方案。