降低解析几何运算量“四化”

广东省吴川市第一中学(524500) 柯厚宝

笛卡尔(Rene Descartes)于1637年创立了解析几何,使得几何问题可以归结成代数问题,也可以通过代数转换来发现、证明几何性质.几何图形的最基本元素是“点”,建立平面直角坐标系,把“点”转换为“坐标”计算是其核心思想.从而“跟踪点坐标”便成了研究解析几何问题的基本方法.然而,我们在跟踪点坐标的过程中常会出现两种情况,一是所跟踪的点坐标是易算或可算的,二是所跟踪的点坐标是难算或不可算的.前者难度不大,但后者若计算方法不当,容易带来极其繁杂的计算,易无果而终.对如何降低解析几何运算量的研究,已有了不少结果,如文[1]、[2],此类文章对于优化解析几何运算在宏观上作了很好的研究,但在实际操作中还稍有欠缺.本文结合笔者的教学实践及研究,梳理一些更具操作性的方法,与同仁交流.

1.弦长问题程序化

直线与圆锥曲线相交,通常涉及弦长的计算.此类问题可将其总结为一种计算程序,降低运算量.

例1 已知直线l经过椭圆C∶的右焦点F,且与椭圆相交于A,B两点,求|AB|的最小值与最大值.

解析椭圆C的右焦点为设直线l∶由得此函数关于t2单调递增,当t=0,即直线AB⊥x轴时,|AB|min=1,当t2→+∞,即直线AB与x轴重合时,|AB|max=4.

点评以上解法重点关注计算(t2+4)y2+-1=0与∆=16(t2+1),其他按程序抄写即可.常规解法还需要把y1+y2=代入计算.另外,若把直线设为运算量稍大,还要讨论的情况.

事实上,对于涉及圆锥曲线弦长的计算问题,我们可作如下程序化处理：

第一步：设出弦所在的直线方程.①直线l过x轴上的点(x0,0)设为x=ty+x0(不含直线y=0); ②直线l过y轴上的点(0,y0)设为y=kx+y0(不含直线x=0); ③直线l过点(x0,y0)(x0,y00)设为y=kx+(y0-kx0)(不含直线x=x0);

第三步：计算弦长.其中a2k2+b2是第二步所得的一元二次方程二次项的系数,k是直线y=kx+m中x的系数.

对于直线x=ty+m与椭圆b2x2+a2y2=a2b2(a＞b＞0)的相交弦长问题,类似地有,|AB|=其中b2t2+a2是所得一元二次方程二次项的系数,t是直线x=ty+m中y的系数.

以上程序也适用于计算直线与双曲线、抛物线的相交弦长问题.

2.双向坐标同向化

涉及线段的长度或直线的斜率问题时,通常会同时出现横向坐标x1,x2与纵向坐标y1,y2,直接计算,运算量较大,可转化为x1,x2或y1,y2进行计算.

例2 (2018年广东二模理)设过抛物线y2=2px(p＞0)上任意一点P(异于原点O)的直线与抛物线y2=8px(p＞0)交于A,B两点,直线OP与抛物线y2=8px(p＞0)的另一个交点为Q,则

图1

解析如图1,设点Q,O到直线OP的距离分别 为d1,d2,则设 直 线OP∶y=kx,由得由得则所以即

点评相似三角形的性质是实现坐标同向化的一个常用工具,本题若直接计算运算量非常大.

例3 过点M(0,1)的直线l与椭圆或相交于A,B两点,且|MB|=2|MA|,求直线l的方程.

图2

解 析(1)当 直 线l与y轴重合时,不合题意;(2)当直线l与y轴不重合 时,如 图2,设l∶y=kx+1,A(x1,y1),B(x2,y2),由得(9k2+4)x2+18kx-27=0,则

① 当k＞0 时,不 妨 设A在x轴 的 上 方,由|MB|=2|MA|得-x2=2x1,即x2=-2x1,所 以消 去x1得解得由k＞0得

②当k＜0 时,同理得

所以直线l的方程是

点评由相似三角形的性质,我们将|MB|=2|MA|转化为-x2=2x1,简化了|MB|与|MA|的计算.一般而言,若直线l过y轴上的定点,需同化为横坐标计算,若直线l过x轴上的定点,需同化为纵坐标计算,若直线l过原点,同化为横坐标或纵坐标计算均可.

例4 (2015年全国卷第20 题第(2)问)已知曲线C∶y=与直线y=kx+a(a＞0)交于M,N两点,O为原点,在y轴上是否存在点P,使得当k变化时,总有∠OPM=∠OPN? 说明理由.

解析存在符合题意的点,证明如下：

设P(0,b)为符合题意得点,M(x1,y1),N(x2,y2),直线PM,PN的斜率分别为k1,k2.由得x2-4kx-4a=0.所以x1+x2=4k,x1x2=-4a.所以k1+k2=当b=-a时,有k1+k2=0,则直线PM的倾斜角与直线PN的倾斜角互补,故∠OPM=∠OPN,所以P(0,-a)符合题意.

点评本题我们用了抛物线方程x2=4y将y1,y2转化为横向坐标x1,x2实施计算,运算量比用y=kx+a将x1,x2转化为纵向坐标y1,y2计算低不少.一般而言,椭圆、双曲线用直线转化,抛物线优先用抛物线转化.

在处理解析几何的计算问题中,经常会遇到涉及双向坐标的计算,如x1x2+y1y2、x1y2+x2y1.|x1y2-x2y1|等,选用对应的方法,将双向坐标同向化,是解决问题的有效途径.

3.同类问题推算化

在对解析几何问题的计算过程中,常会遇到不少同类型的计算问题,只需算好一种情况,其他情况只需对最后结果作简单推算即可得到结果.

例5 (2018年广东二模理第20 题第(2)问改编)若过椭圆的左、右焦点F1,F2分别作两条互相垂直的直线交椭圆于A,B和C,D,设线段AB,CD的长分别为m,n,证明：是定值.

解析可得F1(-2,0),F2(2,0),当直线AB,CD的斜率不存在或为0 时,当直线AB,CD的斜率存在且不为0 时,设AB∶x=ty-2,CD∶x=过点F2作直线l//AB与椭圆相交于M(x1,y1),N(x2,y2),则|AB|=|MN|=m,且MN∶x=ty+2,由得(t2+2)y2+4ty-4=0,则y1+y2=所以|AB|=|MN|=同理得所以综上,

点评本题原本不能由|AB|=m的结果通过同理推算出|CD|=n的,原因是x=ty-2 与并非仅存在t与的差异,但通过过F2作直线MN//AB,根据椭圆的对称性得到|MN|=|CD|,而直线MN的方程为x=ty+2,它与CD∶x=+2 仅存在t与的差异,转化为同类问题,使得所有计算过程类同,实施同理推算,有效降低了运算量.

例6 (2018年广州二模理第20 题第(2)问)过点R(0,2)的直线l与抛物线C∶x2=2y相交于A,B两点,与直线y=-2 交于点M,抛物线C在点A,B处的切线分别记为l1,l2,l1与l2交于点N,若△MON是等腰三角形,求直线l的方程.

解析设直线l∶y=kx+2,A(x1,y1),B(x2,y2),N(x0,y0),由y=得y′=x,则切线l1∶y-y1=x1(x-x1),即y=x1x-y1,所以y0=x1x0-y1,同理得y0=x2x0-y2,所以直线AB∶y0=x0x-y,即y=x0x-y0,又直线l∶y=kx+2,故即N(k,-2),由-1,得OM⊥ON,所以|OM|=|ON|,即所以k=±2,所以直线l∶y=±2x+2.

点评求得切线l1∶y=x1x-y1即可同理推算出切线l2∶y=x2x-y2,又l1,l2均过点N(x0,y0),于是知两点A,B均在直线y0=x0x-y上,两点确定一条直线,故有直线AB∶y=x0x-y0,与l∶y=kx+2 是同一直线,即可得到N(k,-2),从而解决了问题,运算量非常低.

在计算的过程中,若发现计算方法类同时,不必重新计算,只需分析问题的差异,直接从已得到的结果作替换推算即可得到想要的结果.

4.复杂最值换元化

不少解析几何最值问题,通过换元转化可达到化繁为简的效果.但在换元的过程中需关注所换变量取值范围的变化.

例7 已知直线l经过双曲线C∶x2-y2=1 的左焦点F1且与双曲线C的左支交于A,B两点,F2为双曲线C的右焦点,求△ABF2的面积的最小值.

解析设l∶由得

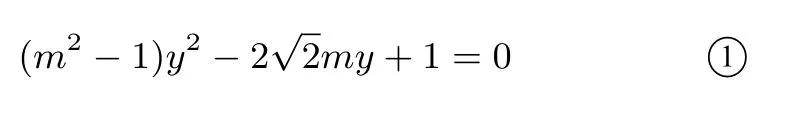
由直线l与双曲线C的左支交于A,B两点,知方程 ①必有一正一负两个实根,所以所以m2＜1,而∆=8m2-4(m2-1)=4(m2+1),

所以

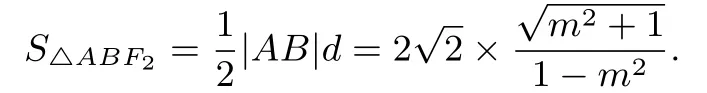
点评对于求型的最值问题,作换元后,可能出现以下三种情形：一是变形为(分子为常数),求h(t)的最值即可;二是变形为h(t)±运用基本不等式或函数单调性可求最值;三是变形为(结构比简单),运用导数研究函数的单调性可求最值.