追根溯源—数列的周期是如何形成的?

广东省江门市培英高级中学(529000) 邹庆榕

周期性是高中数学中函数的一个考点;周期数列是特殊的函数,也是竞赛题中一个考点.但我们对周期数列的有关性质却研究不多.解决周期数列问题一般是通过迭代列举有限项求其周期,但对于周期大的数列,容易被误判为非周期的.本文探索形成周期的两类源头：(1)周角(T=2π)给出数列周期性的判定定理,可直接求周期,避免大量计算; (2)整除(模[1])等有限的背景给出周期数列的例子.

函数的迭代周期概念是现代数学混沌概念产生的基础,另外周期数列在图论,傅里叶级数,动力系统,图像压缩,分形几何等高等数学中有大量应用,值得深入研究.鉴于笔者水平有限,仍有很多周期数列的问题有待研究,如分段函数形式的周期数列和著名的角谷猜想生成的数列等等,希望能与各位同仁共同研究.

定理1 若an+1=(0,n≥ 1),则是以为公比的等比数列,其中x12,都满足x2-Ax-B=0;

(1)若A=0,则数列{an}是周期数列,周期T=2;

(2)若∆=A2+4B＜0,且0,则

①a1=xi(i=1,2),则an=xi(i=1,2);

②记E=则|E|=T-1,aT-1=0;若a1∈E,数列在不超过T-1 项后没有意义;

③记tan|θ|=且存在N ∈Z+,使得且a1/∈E,则数列{an}是周期数列,周期T=N;

证明(1)利用函数思想an+1an=B,an+2an+1=B,两式相除得an+2=an,则T=2.

(2)由xi(xi-A)=B,i=1,2,an+1-xi=则

证毕.

例1an+1=5+

(1)a1=5,求a2018;(2)a1=1,求a2018.

解(1)迭代计算得各项为：不存在,a2018不存在.

例2 已知数列的递推关系为

(1)a1=1,求a2018; (2)a1=i,求a2018;

(3)a1=求a2018; (4)a1=求a2018.

解则T=6,所以a2018=a336×6+2=a2.

1 2 3 4 5 6 7 2018 a1=1■3-1■3-1-1■3+1■3+1 1■3-1 a1= i ■3+i 3■2 3+i 4■3+i 3■3+i ■2 3+i i ■3+i a1=■3+i 2■3+i 2■4 3+i 2■7 3+i 2■7 3+i 2■4 3+i 2■3+i 2■3+i 2 a1=■3 2■3 3■3 2■3 3 0不存在不存在不存在

例3 已知以下数列的递推关系,判断它们是否具有周期性：

解(1)

(2)令cn=an+1,cn+1=转化为(1),则T=3;

(3)换元后同(1);

(4)x2=-x-1,x1,2=tan|θ|=

(5)cn=1-an,cn+1=-2x+2=0,x1,2=1±i,T=4;

(6)换元后同(5);

(7)令cn=1+cn+1=2-x2=2x-4,

(9)cn=1+an,cn+1=T=2;

(10)x2-3x+3=0,x1,2=T=6,本题在参考文献[2]中的证明比较繁琐;

(11)x2=x-2,x1,2=找不到相应的θ,根据定理1 可预测这不是一个周期数列.其通项公式：其中(a12).但它的实用性不强.借助qbasic 等软件,给定a1可以检验这个数列应该无限不循环.事实上给定θ ∈R,并不都可写成整数分之π的形式(如θ=1),这也说明非周期数列是怎么产生的.

定理1 是关于相邻两项分数型的递推关系,它是以正切函数为原型的.对于相邻多项的线性递推关系,我们已有特征根定理[3],再利用欧拉公式得到以正(余)弦函数为原型的定理2：

定理2 数列{un}满足aun+2+bun+1+cun=d,其特征根方程为ax2+bx+c=0,若∆=b2-4ac＜0,记且存在N ∈Z+,使得则数列{an}具有周期性,且最小正周期

证明特征根其中记则对给定u1,u2,存在p,q,s,有un=pxn1+qxn2+s=rpenθi+rqe-nθi+s=r[(p+q)cosnθ+(p-q)sinnθ]+s=其中tan所以周期

实际上定理2 是以正(余)弦函数为原型,因此|θ| ∈(0,π).

例4 已知以下数列的递推关系,判断它们是否具有周期性：

(1)an+1+an-1=0; (2)an+1=an-an-1;

(3)an+1+an+an-1=6; (4)an+1×an-1=an.

解(1)x2+1=0,x1,2=±i=事实上,存在p,q,s,an=in[p+(-1)nq]+s,显然T=4;

(2)x2=x-1,x1,2=所以

(3)x2+x+1=0,x1,2=所以

(4)两边取对数后同(2).

下面我们来看3 个“有限”背景的问题：

例5a1=3,a2=1,当n≥1 时,an+2等于an·an+1的个位数字,则求a2018.

逐项计算数列的项可知周期为6,则a2018=a2=1.

但是学生问,若首两项改变了,它还是周期数列吗? 这是一个“有限”问题(个位数只有10 个数,也说明这个数列最多只是这10 个数的排列组合问题),只要相邻两项重复出现一次就能说明周期性,周期不会超过A210.考虑到若首2 项若有5,则数列从第3 项起恒为0 或恒为5,则不考虑首2 项有5 的情况.记[x]为10 的同余类[1],即[x]={t|t-x整除10},由整除性[xy]=[x][y],[xn]=[x]n,问题转化为[an+2]=[an·an+1].

实际上,记A={1,2,3,4,6,7,8,9},O={1,3,7,9},B={2,4,6,8},an+6=an+5· an+4=a2n+4· an+3=a2n+4·an+2·an+1=a2n+4·a2n+1·an=a2n+3·a2n+2·a2n+1·an=a4n+3·an,则

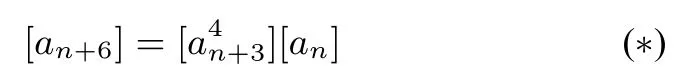
显然若b ∈B,c ∈O：[6×b]=[b],[b4]=6,[c4]=1.

①a1和a2∈O：则an ∈O,an+3∈O,[a4n+3]=1,则由(∗)式[an+6]=[an];

②a1或a2∈B：则an ∈B,an+3∈B,[a4n+3]=6,则由(∗)式[an+6]=6×[an]=[an](n≥3).

综上可知,1°首2 项都是奇数时,是周期为6 的数列;2°首2 项有偶数时,去掉前2 项后是周期为6 的数列.

可以验证，共有6个顺时针的“封闭列”：

例6（2011年高考江西卷文科第6题）观察下列各数：的末两位数字为多少？

解法1计算则所求为43；

解法2因为又所以下同.

例7是的小数点后第n位数，求

解逐个计算可得周期为3，答案为1.事实上，个位数是从0～9这10个数字中选取，的表达式中没有数字0，而且有2个4，因此与此4相关的位数循环形成周期.