“合一”何须“分二”—例谈数学解题中的“整体”策略

江苏省姜堰第二中学(225500) 张新志 周春霞

数学解题重在两大能力,一是审题能力,学会审题,即要知道问题给出哪些信息—关键词与数量关系,还需要把握问题的结构(算法结构、联系结构、空间结构、策略结构等),为解题制定策略打下基础;一是运算能力,学会观察运算方向、运算简化途径等,还需要从整体上认识问题、把握问题本质.

整体思想是指在数学解题时,站在整体的立场上心怀全局,注重对局部研究的同时,通过研究整体的结构和形式,把握数学问题的本质,寻找解决问题的途径.在高中数学的解题教学中,整体思想可以让复杂的问题简单化,突破学生的思维障碍,提高数学解题的速度,现从审题、解析、解读三个角度体验整体思想在高中数学核心知识(数列、函数、三角函数、立体几何、解析几何)的应用.

1.在数列中的应用—整体变形与运算

等差等比数列的通项公式及前n项和公式,共涉及五个量a1,an,d(q),n,Sn,知道部分量求其它未知量,就体现了用方程的思想解决问题.数列的通项公式和前n项和公式在解题中起到变量代换作用,用两个基本量表示已知和未知是常用方法,如果整体看待式子,整体变形和运算,解题将会收到奇效.

例1 在各项均为正数的等比数列{an}中,a1+a2+a3+a4+a5=4,a21+a22+a23+a24+a25=3,则a1-a2+a3-a4+a5=____.

审题可以设数列的公比为q,数列{a2n}也是等比数列,利用等比数列求和公式写出前两个等式,所求也为等比数列,利用整体思想即可快速求解.

解析设数列{an}的公比为q,由已知得到则所以4S=3,S=即a1-a2+a3-a4+a5

解读乍眼一看,此题是等比数列问题,运用基本量就可以解决,正所谓“一叶障目”,没有从整体上看问题,许多学生都是设基本量,利用解方程组的方法进行求解,致使无数考生“误入歧途”,所以从结构上认识变量间联系,整体上处理是一种数学智慧.

例2 在等比数列{an}中,若a1+a2+a3+a4=8,则a1a2a3a4=____.

审题利用等比数列的前n项和公式写出两个等式,两式相除,再进行平方即可求出值.

解析设数列{an}的公比为q,由已知得到两式相除得到a21q3=4,a1a2a3a4=a41q6=16.

解读本题采用化“二”为“一”的整体思想,两式相除是关键,再接下来观察所求式子的形式为相除所得等式的平方.

2.在函数性质中的应用—整体把握函数结构

“双层”最值函数问题一直是各种考试的热点,因为其具有一定的综合性,对学生的能力要求比较高,所以深受命题者的青睐.解决此类问题的策略大多是引入变量,建立函数关系,从里到外、循序渐进、逐层突破.笔者采用整体研究的解题策略,从整体研究内层函数,结合不等式再研究外层最值函数.

例3a＞0,b＞0,c＞0,记M的最小值是____.

审题本题要求两个表达式的较大者的最小值,解题策略是把相加,再利用基本不等式求出M的最小值.

解析由题意知所以2M≥所以M≥2,当且仅当a=b=c=1 时等号成立,故M的最小值为2.

解读本题涉及“双层”最值问题,内层两个表达式都涉及三个变量,单独的求某一个表达式最值则无从下手,根据max{x,y}的含义把两个表达式整体相加,再利用基本不等式求出M的最小值.

例4 已知a＞0,b＞0,且其中min{a,b}表示数a,b中较小的数,则h的最大值为____.

审题根据min{a,b}的含义,将不等关系转化为再结合基本不等式求出h的最大值.

解析由题意知,0＜h≤a,所以当且仅当即时等号成立.

解读审题发现题目条件不足,思维遇到障碍,切忌纠结单个表达式,分层构建不等关系是本题的关键,再利用基本不等式求出最大值,解题策略是抓住整体特点,巧妙构思,局部量有着整体上的联系,直接从整体出发去解决问题.

3.在三角函数中的应用—整体代换或配置

三角函数是高考必考内容,命题规律为通过拆角凑角等方法,利用两角和与差的正余弦公式直接求值.分析所求角和已知角的关系,用整体代换的思想,建立已知和未知的桥梁,巧妙的求出三角函数的值.

例5 已知cos求cos(α+β)的值.

审题观察已知角和所求角α+β的关系,得出利用两角差的余弦公式求出的值,由倍角公式求出cos(α+β)的值.

解析因为所以所以sin又所以

所以cos(α+β)=

解读利用“拆角”的方法对α+β进行分拆,再由整体代换的思想进行求值.由角的范围求其三角函数值采用“两步”策略,第一步确定角的范围,第二步由已知的三角函数值,利用同角三角函数的关系求其它三角函数值.

例6 求cos 20°cos 40°cos 80°的值.

审题三个余弦函数值,一般都是从角度间的联系入手解决问题.换一个视角,从三角函数配对是否可以有新的突破呢?

解析设x=cos 20°cos 40°cos 80°,y=sin 20°sin 40°sin 80°,则

0,所以

解读观察所求式子的特点,三个角成等差数列,采用整体策略,设出三个角的正弦的乘积,再利用倍角公式和诱导公式进行求值.

4.在立体几何中的应用—整体处置或补形

立体几何是高中数学核心知识之一,表面积和体积常被考察的知识点,考查类型往往是定型和定性,往往通过三视图和折叠与其它几何体相结合的组合体的样式呈现,这类题目对空间想象要求较高.通过两例谈谈用补形的方法,完善几何体,利用整体思想使问题简便求解.

例7 (2018年高考新课标I 卷理科第10 题)图1来自古希腊数学家希波克拉底所研究的几何图形,此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB,AC.△ABC的三边所围成的区域记为I,黑色部分记为II,其余部分记为III,在整个图形中随机取一点,此点取自I,II,III 的概率分别记为p1,p2,p3,则()

A.p1=p2B.p1=p3C.p2=p3D.p1=p2+p3

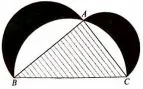
图1

审题首先设出直角三角形的三个边长分别为a,b,c,根据其为直角三角形得到三边的关系,求出各个区域对应的面积,再根据面积的大小根据几何概型的概率公式确定p1,p2,p3的关系,从而得到关系.

解析设AC=b,BC=a,AB=c,则有a2=b2+c2,△ABC的面积为黑色部分的面积为S2=其余部分的面积为所以p1=p2,选A.

解读结合数学史呈现的题目很耀眼,黑白对比强烈,阴影部分为对应的半圆面积减去对应弓形面积,而单独求每个弓形的面积又比较困难,若把整个弓形看作为一个整体,把整个阴影部分看作为一个整体,则弓形的面积为以BC为直径的半圆的面积减去△ABC的面积,阴影的面积为以AB,AC为直径的半圆的面积和减去弓形的面积,即可得到选项.

例8 已知正四面体的棱长为四个顶点在同一个球面上,求此球的表面积.

审题一个特殊的几何体—正四面体,有许多特殊的位置关系与度量关系,与正四面体相关联的几何体是正方体,是否可以从整体上突破呢?

解析如图2将四面体补成正方体,则正方体的棱长是1,正方体的体对角线的长为则球的表面积为

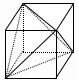
图2

解读本题的解题策略是把四面体补成正方体,二者的外接球是同一个,正方体的体对角线的长,就是球的直径,利用整体思想,求出球的表面积.

5.在解析几何中的应用—合二为一整体处置

解析几何不仅涉及几何知识,更多的涉及代数知识,因为其综合性较强,能力要求较高,是各级各类考试的必考题.解法无非是几何法和代数法,然而学生在解决这类题目往往会受阻,终究是解题方法和思维的受阻,从这个角度而言就需要合“二”为“一”的整体教学策略的养育.

例9 已知圆C∶x2+y2-2x+4y-4=0,直线l的的斜率为1,且l被圆C截得弦AB,若以AB为直径的圆过原点,求直线l的方程.

审题设出过点A,B的圆系方程,再由圆以直线l与圆C的相交弦AB为直径,得到所求圆的半径最小,即2λ2-(4b+12)λ+36 的值最小,半径最小时λ=b+3,再由圆过原点得到λb=4,解方程求出直线方程.

解析设直线l的方程为y=x+b,设过点A,B的圆的方程为x2+y2-2x+4y-4+λ(x-y+b)=0,整理得到圆的方程为x2+y2+(λ-2)x+(4-λ)y+λb-4=0,又圆以AB为直径,所以(λ-2)2+(4-λ)2-4(λb-4)=2λ2-(4b+12)λ+36的值最小,由二次函数的单调性知λ=b+3 时最小,又因为圆过原点,所以λb=4,即(b+3)b=4,所以b=-4 或1,当b=-4 时,圆心到直线的距离b=1 时,圆心到直线的距离所以直线l的方程为x-y+1=0 或x-y-4=0.

解读遵循常规思路,首先设出直线方程,再把直线和圆联立方程组进行消元,再设出点的坐标A(x1,y1),B(x2,y2),再利用=x1x2+y1y2=0,利用韦达定理求出直线方程.这种方法运算量偏大,对学生的运算能力要求较高,设出圆系方程,利用整体思想,简化运算.

例10 (2018年高考新课标I 卷理科第19 题)设椭圆的右焦点为F,过F的直线l与C交于A,B两点,点M的坐标为(2,0).

(1)当l与x轴垂直时,求直线AM的方程;

(2)设O为坐标原点,证明：∠OMA=∠OMB.

审题首先对直线的倾斜角进行讨论,再设直线的方程,采用设而不求的方法,考虑到kMA+kMB=0,再由x1x2,x1+x2的整体性,利用韦达定理整体代入证明.

解析(1)略; (2)当直线l与x轴垂直或重合时,∠OMA=∠OMB,当l与x轴不垂直时,设直线l的方程为y=k(x-1),A(x1,y1),B(x2,y2),直线MA,MB的斜率之和为kMA+kMB=将直线代入得,(2k2+1)x2-4k2x+2k2-2=0,x1+x2=代入2kx1x2-3k(x1+x2)+4k==0,所 以∠OMA=∠OMB.

解读常规方法是设出直线方程,再把直线和椭圆联立方程消元后,用直线的斜率表示出点A,B的坐标,再利用kMA+kMB=0 证明∠OMA=∠OMB,此种做法运算量大.巧妙的采用设而不求的整体策略,首先确定证明的突破口,再由结构的整体性优化解题思路.

从上述各问题的审题—解析—解读可见,整体性教学要求教师在教学中灌输“整体”到“局部”再到“整体”的教学整体思想,先对问题的结构和形式进行审题,纵观全局研究问题,把握“题眼”,正所谓见了树木又见森林.采取化“二”为“一”的解题策略,反其道而行之,化难为易简化运算,注重视角调整力促问题解决.