对圆锥曲线中一类定值问题的探究

江苏省无锡市运河实验中学(214000) 韩 郡

笔者现举出一道模拟题对其中一类定值问题的背景进行探索研究.

图1

模拟题如图1,已知椭圆的离心率且经过点抛物线C2∶x2=2py(p＞0)的焦点F与椭圆C1的一个焦点重合.

(I)过F的直线与抛物线C2交于M,N两点,过M,N分别作抛物线C2的切线l1,l2,求直线l1,l2的交点Q的轨迹方程;

(II)从圆O∶x2+y2=5 上任意一点P作椭圆C1的两条切线,切点为A,B,证明：∠APB为定值,并求出这个定值.

解(I)略;

(II)在第一问可以求出椭圆标准方程为：

① 当两切线的之一的斜率不存在时,根据对称性,设点P在第一象限,则此时P点横坐标为代入圆的方程得P点的纵坐标为此时两条切线方程分别为此时∠APB=若∠APB的大小为定值,则这个定值只能是

综上可知：∠APB的大小为定值得证.

通过上题,我们发现在上述圆上任取一点P作椭圆的两条切线,那么这两条切线相互垂直.

思考如果作给定椭圆的两条相互垂直的切线,那么两条切线的交点的轨迹是否是一个定圆?

变式如图2,已知椭圆C1∶过椭圆外一点P(x0,y0)作直线l1,l2分别于椭圆C1相切于A,B两点,且l1⊥l2,证点P在一个定圆上,并求出轨迹方程.

图2

证设过点P(x0,y0)的直线方程为：y-y0=k(x-x0),联立椭圆方程代入整理得：(a2k2+b2)x2+2ka2(y0-kx0)x+a2k2x20-2ka2x0y0+a2y20-a2b2=0,∆=4a2k2(kx0-y0)2-4a2(a2k2+b2)[(kx0-y0)2-b2]=0,经化简得：(kx0-y0)2=a2k2+b2,继续整理成关于k的一元二次方程：(x20-a2)k2-2x0y0k+y20-b2=0,因为过点P作的两条切线l1⊥l2,所以k1k2=-1,根据韦达定理得：x20+y20=a2+b2.当其中一条切线斜率不存在时,点P坐标为(a,b)在上述圆上.所以点P在以原点为圆心,为半径的圆上,圆的方程为x2+y2=a2+b2.

结论1 对于给定椭圆作椭圆两条相互垂直的切线,两条切线的交点的轨迹为一个定圆,定圆的方程为x2+y2=a2+b2.我们把这个定圆称为椭圆的“伴随圆”.同样地,如果取圆x2+y2=a2+b2上任意一点,作椭圆的两条切线,那么这两条切线互相垂直.

笔者对定圆进一步研究发现,如果延长其中一条切线交定圆为点Q,则

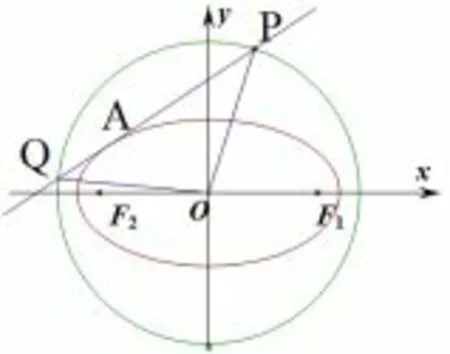
图3

证明如图3,设椭圆的切线方程为y=kx+m,直线与圆O∶x2+y2=a2+b2的两交点为P(x1,y1),Q(x2,y2),联立椭圆方程整理得：(a2k2+b2)x2+2kma2x+a2m2-a2b2=0,因为直线与椭圆相切,所以∆=4k2m2a4-4a2(m2-b2)(a2k2+b2)=0,即

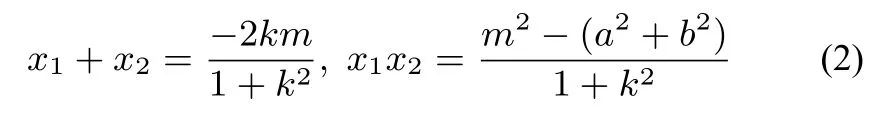
结论2 椭圆的一条切线与其“伴随圆”相交于P,Q两点,则

此时再回顾一开始的模拟题第二问求∠APB为定值,我们现在直接利用结论2 就可以快速得出结果：

方法二如图4,设过点P的两条切线分别与圆相交的两个交点为Q,S,由结论2 可知,kOP kOQ=同理可得kOP kOS=则kOQ=kOS,则O.Q.S三点共线,所以QS为圆O的直径,即

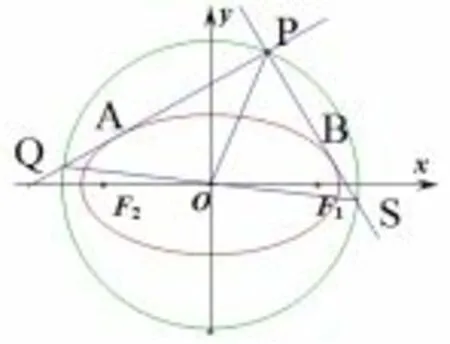
图4

下面笔者给出两道模考题,供读者练习使用：

(I)求椭圆C的方程;

(II)设P为圆E∶x2+y2=4 上任意一点,过点P作椭圆C的两条切线l1,l2,设l1,l2分别交圆E于点M,N,证明：MN为圆E的直径.

(1)求椭圆C的方程和“伴随圆”E的方程;

(2)过“伴随圆”E上任意一点P作椭圆C的两条切线PA,PB,A,B为切点,延长PA与“伴随圆”E交于点Q,O为坐标原点.

①证明：PA⊥PB;

②若直线OP,OQ的斜率存在,设其分别为k1,k2,试判断k1k2是否为定值,若是,求出该值;若不是,请说明理由.