Si3 N4结合SiC耐火陶瓷裂纹萌生细观数值分析

袁 虎，杨自春，赵 爽，孙文彩

(1.海军工程大学 舰船高温结构复合材料研究室，湖北 武汉 430033；2.海军工程大学 动力工程学院，湖北 武汉 430033)

1 引 言

Si3N4结合SiC耐火陶瓷性能优良，广泛运用于船舶增压锅炉炉膛耐火砖内衬等重要结构中。但其具有高脆性，在高低温腐蚀、机械振动、烟气冲刷和热冲击等恶劣环境中承受载荷时，裂纹将由应力高度集中的裂纹尖端迅速扩展开来，且不能通过塑性变形得到松弛。因此，探究该类材料在高温环境工况下的受热损伤的机理，寻求此类材料抗高温疲劳损伤的改良方案，无论对延长材料的使用寿命和还是提高所应用设备的运行安全稳定性，都具有较大的参考意义。

Shihua Nie等[1]根据材料的微观结构，综合其界面转变区及宏观有效性能，探究了颗粒状复合材料的损伤机理；C.Vinet等[2]提出的细观力学基本损伤模型，将材料的损伤与微裂纹的尺寸、密度等微观参数很好地关联起来；甘荣飞等[3]结合材料的细观均匀性，对其变形性、损伤性和失稳性等破坏过程进行数值模拟；郑恒伟等[4]结合Esheby均匀弹性体中球形夹杂区的内、外应变场，建立了可预测复合材料相关特性的细观力学损伤模型；袁硕伟等[5]在Voronoi网格基础上选用Eshelhy等效夹杂理论，建立了增压锅炉耐火砖衬的微观结构模型，通过表征材料在不同数量级粒径下的颗粒，较好地解释了耐火陶瓷受热冲击时的损伤机理。

应力-应变曲线是材料力学性能在受载环境下的重要表征。近年来，曹卉等[6]运用分子动力学方法，探究了γ-TiAl合金在不同加载速率下的应力-应变关系；邵彬彬等[7]在常温下通过冲击力学实验，探究了不同短切碳纤维含量的C/SiC陶瓷基复合材料的动态应力-应变关系。迄今为止，在连续变化的环境工况下运用试验方法直接求取材料温度与力学性能之间的关系还尚未成熟[8-9]。

本研究基于Si3N4结合SiC耐火陶瓷在不同受热损伤环境下的应力-应变关系，对其损伤过程进行细观模拟。并对离散温度下材料的损伤性能进行探究，以求取高温条件下该类材料受热损伤参数与界面相参数之间的函数关系。

2 细观损伤模型的建立

2.1 复合球模型

为方便运用完美粘合的本构关系描述非完美粘合界面等效力学性能，将材料三相复合系统中的SiC颗粒相和界面相结合，以生成复合球模型，如图1所示。模型中，材料具有各向异性，可认为球形颗粒间的力学性能通过球形界面进行传递。结合材料抗拉和抗压损伤特性，为方便从细观角度描述相互作用的球形颗粒对粘合不完美的两相复合材料的等效力学性能和材料从界面完全粘合到完全脱粘状态的过程，首先将基质相与结合后的颗粒相的弹性模量比定义为界面相参数q。相关参数的表达式见下式[10]。

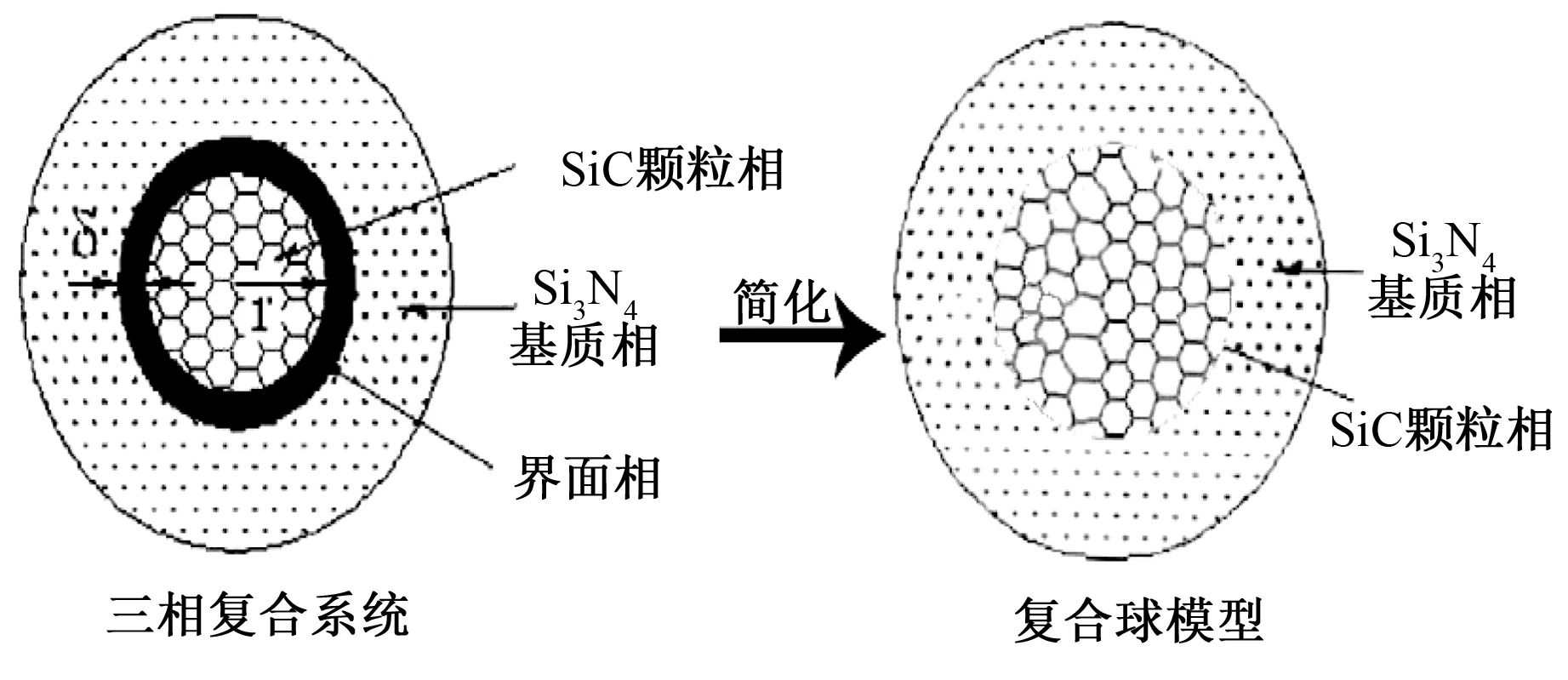
图1 复合球模型的建立过程Fig.1 Establishment process of composite sphere model

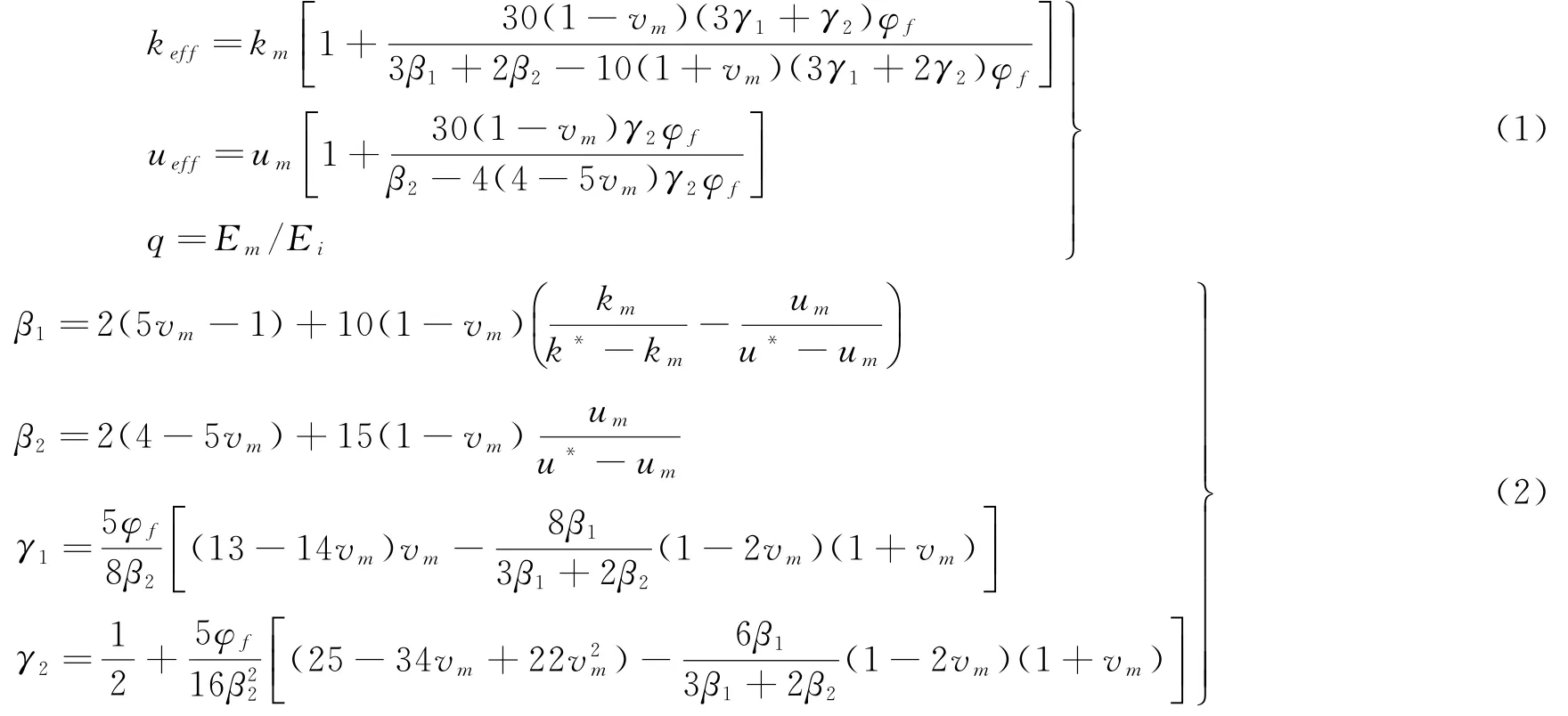
k、u、E和v分别为材料的体积模量、剪切模量、弹性模量和泊松比；φf是填充颗粒的体积分数；E为弹性模量；β1、β2、γ1、γ2可由式(2)中的方程组联立求解得；下标m和i分别代表Si3N4基质相和同界面相结合后的SiC颗粒相；k*和u*分别为体积模量和剪切模量的等效量。

2.2 损伤模型

为方便表示各参数间的关系，本研究在复合球模型的基础上引入弹性模量E的变化来定义损伤参数D。

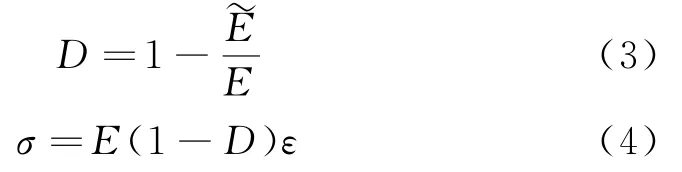
式中，E～为材料受损伤后的弹性模量；σ为试件所受外界载荷；ε为外界载荷作用下所产生的应变。

结合复合球模型和损伤模型不难看出，当q=0时，材料各相界面之间完美粘合；当q→∞时，试件各相逐渐脱粘[11-12]。

3 确定相关物性参数

Si3N4结合SiC耐火陶瓷的相关物性参数如表1所示[13]。

表1 Si3 N4结合SiC耐火陶瓷物性参数Table 1 Physical properties of Si3 N4 Bonded SiC Refractory Cerimic

4 受热损伤模拟

高温环境下，Si3N4结合SiC耐火陶瓷的力学性能受温度影响十分显著。根据物理假设对离散温度点下的损伤性能进行模拟，可使问题得到简化：材料高温下的初始弹性模量将降低、弹性模量变化范围将减小；材料在高温下产生的初始应力趋于损伤极限；各相热膨胀系数在任意相同温度下无明显变化；材料在受拉时的应变区间为[0，0.0006]，受压时的应变区间为[-0.0032，0]。

基于上述假设，结合锅炉炉膛升降温的运行工况，本研究将分别对拉压载荷下材料的受热损伤过程进行数值模拟。

4.1 模拟的过程

运用复合球模型的简化，确定颗粒相和基质相的弹性性能以及各相的体积分数；

计算温度为T时的损伤起始应力σ[14]：

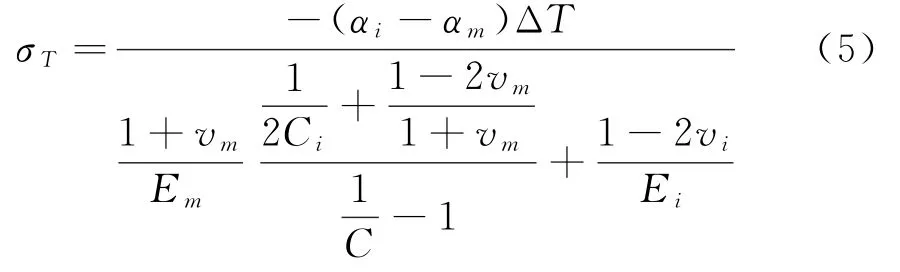
式中，ΔT为室温和试验温度之间的温度差，C为材料常数。

T温度时对应于临界热膨胀系数αc下的材料破坏时的临界应力σfT为[14]：

若αm＜αi，损伤发生在颗粒相和基质相之间的界面处；若αm＞αi，损伤发生在基质相。

根据物理假设，求取任意温度下的起始应力值和达到破坏时的临界应力值，模拟任意温度下材料的应力-应变曲线。

根据材料的应力-应变曲线，推导其弹性模量-应变曲线，并模拟界面参数-应变曲线，从而求取损伤参数与界面参数的联系。

4.2 受拉损伤模拟

选取炉膛负荷突增时，Si3N4结合SiC耐火陶瓷迎火面自然冷却后的稳定温度(439℃)进行受拉损伤演化模拟。结合表1和式(5)，求得此时材料中的初始热应力：σ439=9.46MPa。根据式(6)，进一步求取该温度下材料承受载荷破坏时的应力值。根据物理假设，可将材料的应变分6档计算，模拟出的应力-应变曲线如图2所示，表达式见下式：

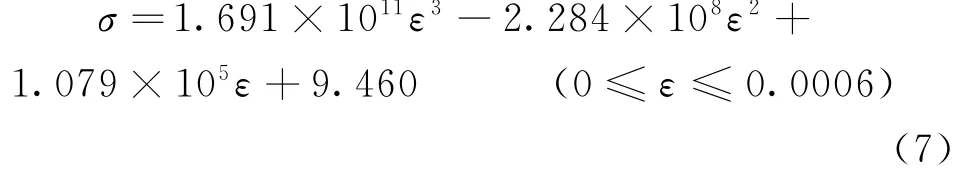
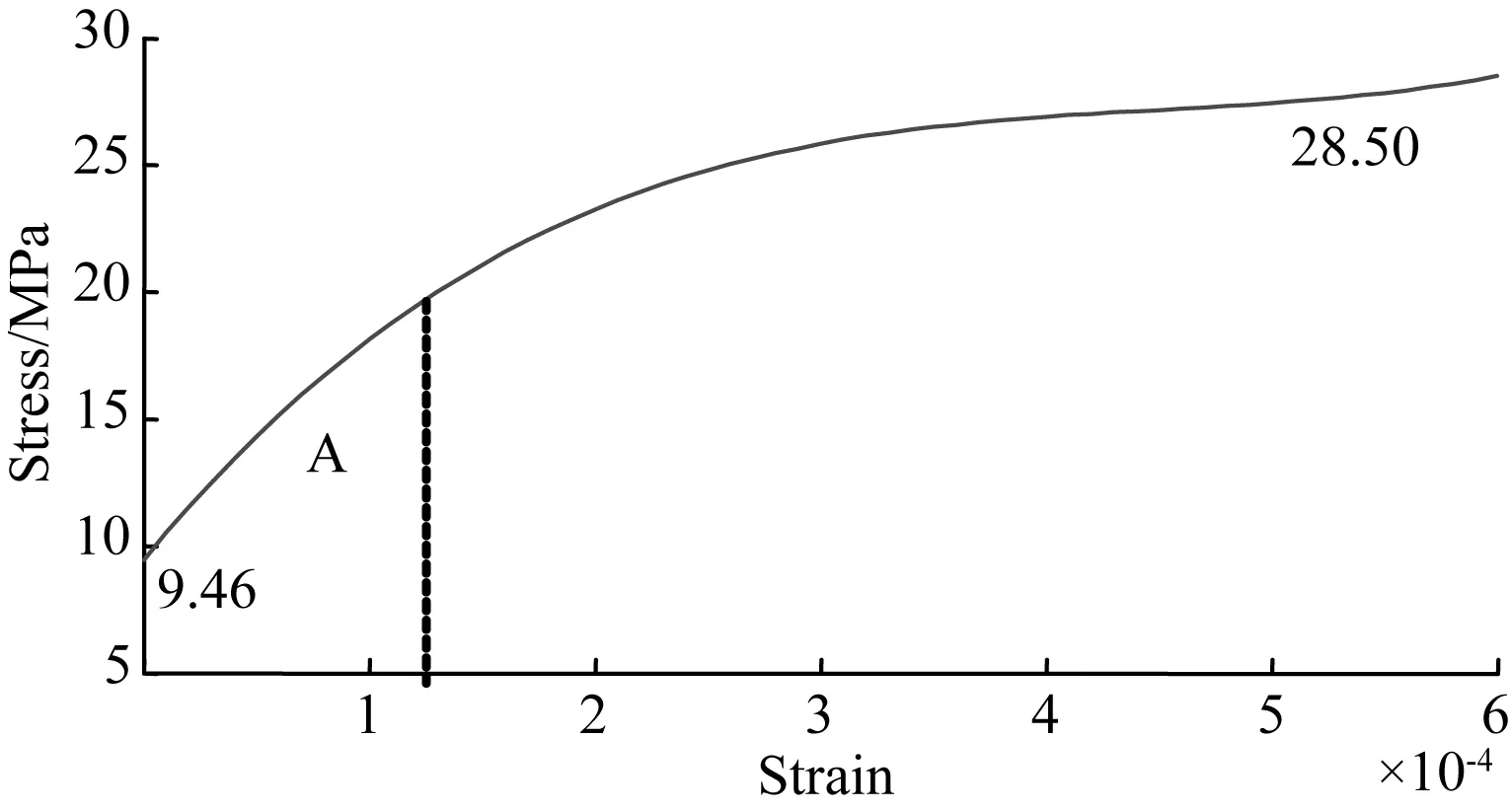
图2 耐火陶瓷439℃时的应力-应变曲线Fig.2 Stress-strain curve at 439℃

从图2可见，较小应变时，曲线是线性的，如图中A区域所示。过了这一阶段后，曲线即表现出很强的非线性，在应变为6×10-4时，应力为28.50MPa，达到最大。

根据式(7)推导材料的弹性模量-应变曲线如图3所示，其关系见式(8)，从中可知，材料的弹性模量随着应变的增加总体呈下降趋势，最后略有上升。

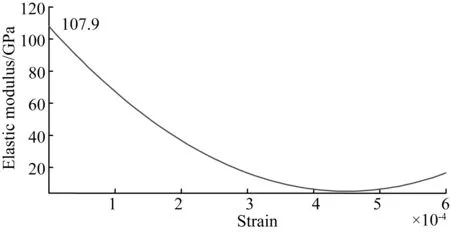
图3 耐火陶瓷439℃时的弹性模量-应变曲线Fig.3 Elastic modulus-strain curve at 439℃

将上述关系式与复合球模型相结合，可模拟出如图4所示的弹性模量与界面相参数q的关系。

将图3中的应变区间划分为若干个点对应到图4上，可得到若干个439℃时的界面相参数值，进而可推知应变与界面参相数的对应关系，如表2。

根据表2，拟合应变ε关于1gq的3次多项式，曲线如图5所示，所得表达关系见式(9)。

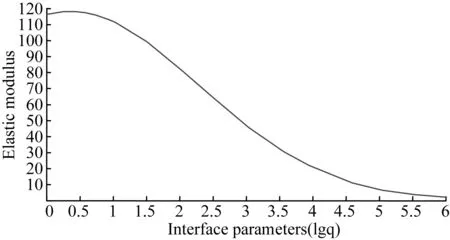
图4 弹性模量与界面相参数间的关系Fig.4 Relationship between elastic modulus and interface phase parameters

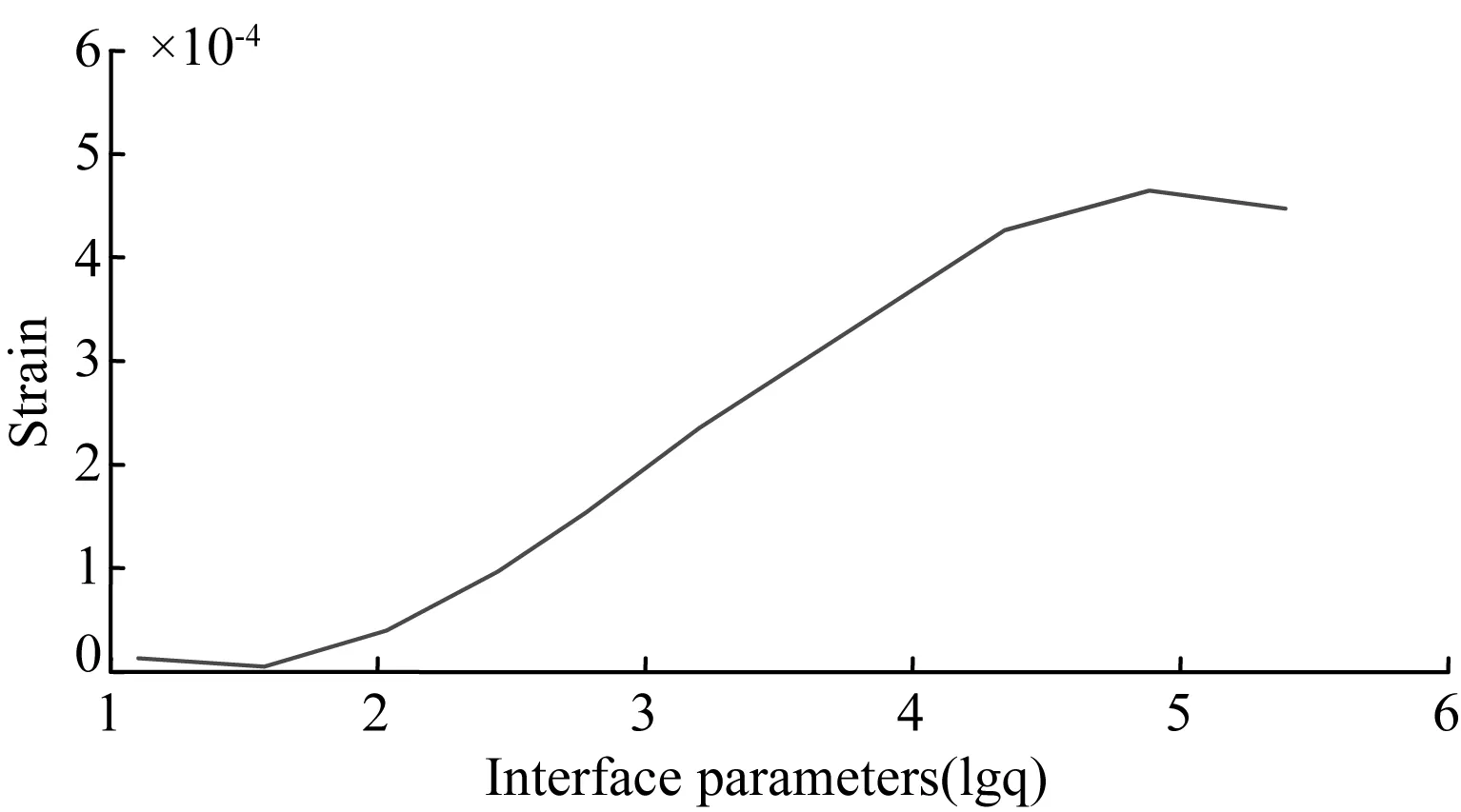
图5 界面相参数与应变的关系Fig.5 Relationship between interface parameters and strains

表2 应变和界面相参数q的对应关系Table 2 Corresponding relationship between strains and interface parameters q

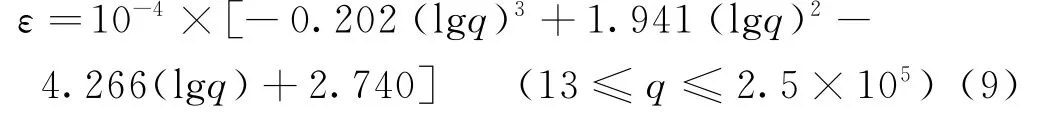
将式(8)导入式(3)，求取的损伤演化方程式：

结合式(9)和(10)，可得到Si3N4结合SiC耐火材料439℃时受拉损伤演化方程式为：

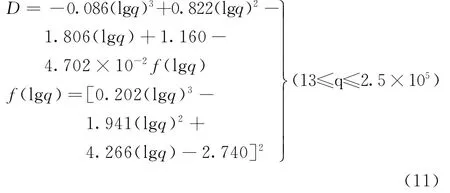
从Si3N4结合SiC耐火陶瓷受拉损伤模拟中可知，当拉应力小于临界值时，材料弹性模量达到最大，但内部没有损伤演化，所有裂纹只发生弹性变形，不发生扩展，即为细观损伤的线弹性阶段。当拉应力在临界值与材料的最大承载值之间时，材料的损伤主要是非线性的，内部发生连续分布的损伤，即已到达损伤非线性强化的阶段。随着外界载荷的增加，应力一旦超出界面强度极限，越来越多的微裂纹将在界面处出现并扩展，最终导致材料界面脱粘，甚至均匀开裂，丧失承载能力。

4.3 受压损伤模拟

选取炉膛负荷突降时，Si3N4结合SiC耐火陶瓷迎火面的中间温度(1200℃)和最高温度(1546℃)情况下分别进行受压损伤演化模拟。根据式(5)，求得此时试件的初始热应力分别为：σ1200=-26.93MPa、σ1546=-34.91MPa。根据式(6)，分别求取两个温度点下试件承受压载破坏时的应力。本处首先模拟1200℃时耐火材料的受压损伤情况。根据物理假设，可将材料的应变区间分为10档计算，模拟出的应力-应变曲线如图6所示，其关系式见式(12)：

结合式(10)推导出试件弹性模量与应变之间的关系，其曲线如图7所示，关系式见式(13)，当-0.0032≤ε≤0时：

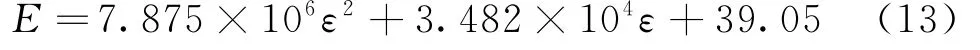
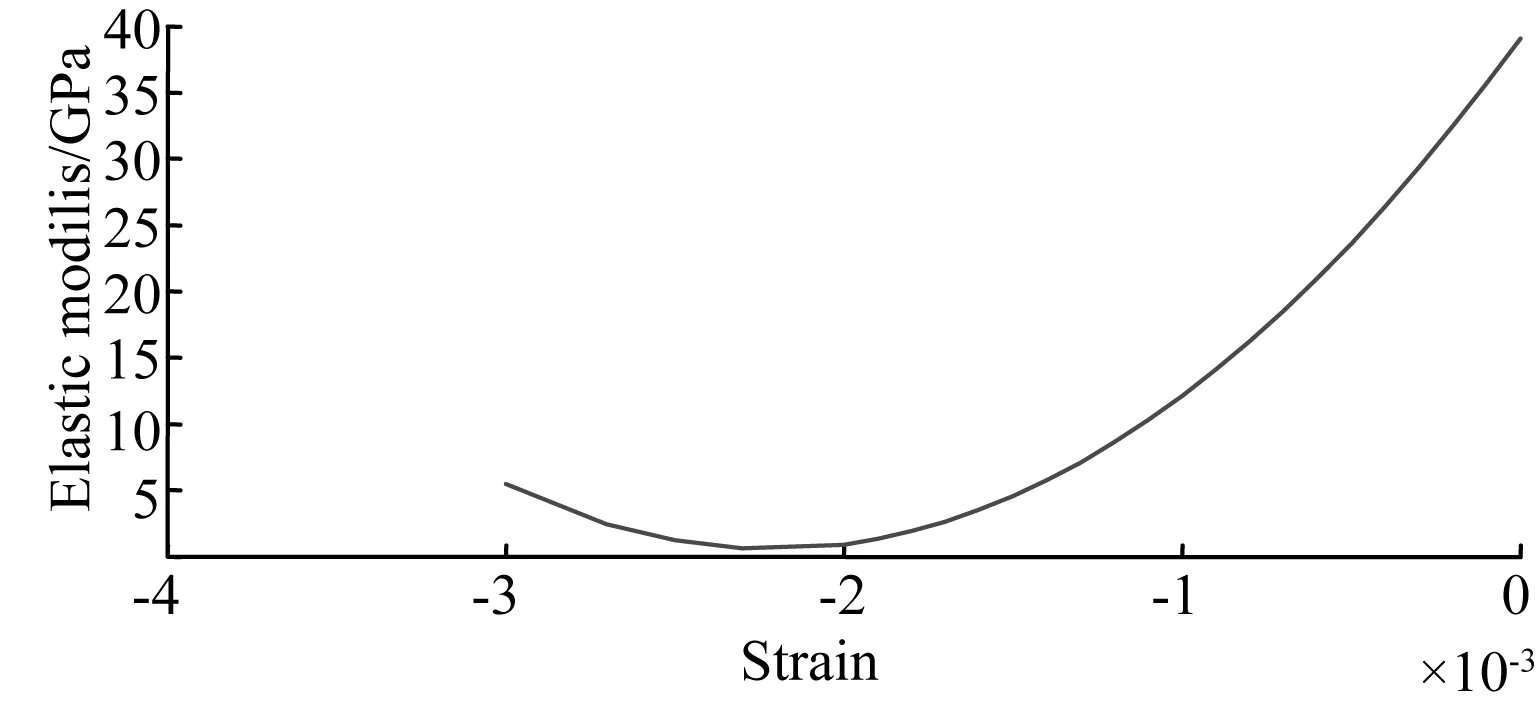
图7 炉膛耐火陶瓷1200℃时的弹性模量-应变曲线Fig.7 Elastic modulus-strain curve at 1200℃

在图7中将应变区间划分为若干个点对应到图4上，可得到若干个1200℃时的界面参数值，进而可推出应变与界面参数的对应关系见表3。

根据表3中的数据，拟合应变ε关于lgq的3次关系式，曲线如图8所示，所得的表达式见式(14)，当103≤q≤8.0×105时：

表3 应变和界面相参数q的对应关系Table 3 Corresponding relationship between strains and interface parameters q

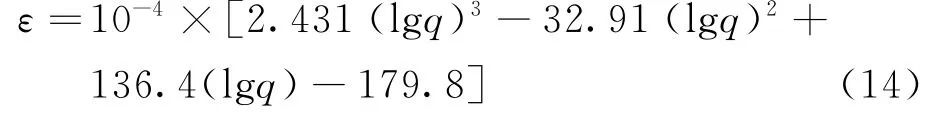
将式(13)导入式(3)，求得的损伤演化方程为式(15)，当-0.0032≤ε≤0时：

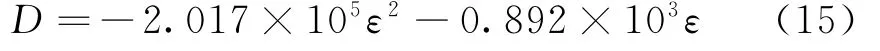
结合式(14)和(15)，求取Si3N4结合SiC耐火材料439℃时受压损伤演化方程，当103≤q≤8.0×105时：

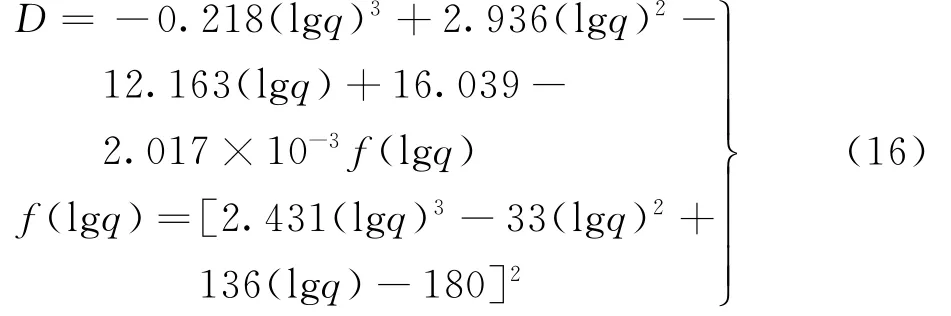
同理，也可模拟出1546℃时Si3N4结合SiC耐火材料的损伤演化方程，见下式，当97≤q≤8.2×105时：

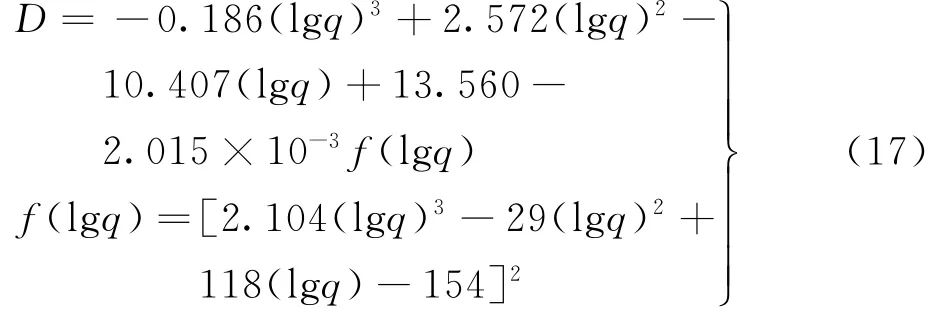
从Si3N4结合SiC耐火陶瓷受压损伤模拟中可知，当压应力小于临界值时，试件的弹性模量也最大，材料仍处于损伤破坏的线弹性阶段，如图6中B区域所示。当压应力在临界值与材料的最大承载值之间时，虽然损伤趋于平缓，但已达到非线性损伤强化阶段。由于此类材料的界面强度高于基质强度，受压时基质将先出现微裂纹并传递至界面。基体裂纹出现后将很快聚集成核，随后扩展至稳态尺寸。

在实际工况中，Si3N4结合SiC耐火陶瓷受热损伤后的断口形貌如图9所示。从中选取任一条裂纹进行分析，可见，基体裂纹首先在箭头A所指的孔隙等缺陷处聚集成核，随后沿B箭头所指的路径扩展至稳定尺寸。在此过程中，微裂纹不断形核、扩展，最终导致界面脱粘，间接证明上述研究的可靠性。

图9 Si3 N4结合SiC耐火陶瓷的断口形貌照片Fig.9 Fracture surface morphology of Si3 N4 Bonded SiC refractory ceramic

5 结 论

本研究将Si3N4结合SiC耐火陶瓷的三相复合系统简化为复合球模型，引入损伤模型中从细观角度求取了材料受热损伤时的界面相参数与损伤参数之间的函数关系，得出了如下定量描述此类材料裂纹萌生机理的一般性结论：

1.在受热损伤时，Si3N4结合SiC耐火陶瓷在高温下的抗压强度比抗拉强度大得多，因此，在此类材料实际应用中应尽量避免温度骤冷造成的剧烈冲击；

2.无论承受拉载还是压载，当σ＜σC和σC＜σ＜σ∞时，此类材料都先后经历着无损伤演化的线弹性阶段和微裂纹扩展区逐渐增大的损伤强化阶段，此时应采取降低外载等积极措施，预防或延缓损伤进一步加剧；

3.若应力达到最大承载值后仍继续增大，某些取向上的微裂纹将穿越晶界的束缚发生二次扩展，导致材料的损伤过渡到损伤局部化阶段，微裂纹损伤局部化的连续即是材料宏观裂纹萌生的开始，此时应加强对材料性能的监测力度。