三点弯曲模式下C/SiC复合材料界面脱粘强度的数值模拟

宿树达，任成祖，李远辰

(天津大学先进陶瓷与加工技术教育部重点实验室，天津 300072)

1 引 言

连续纤维增韧陶瓷基复合材料具有耐高温、低密度、高比强、高比模、抗氧化和抗烧蚀等优异性能，近年来成为航空航天等国防装备发展不可缺少的新型战略性材料，在航空发动机热端部件，如喷管、燃烧室、涡轮和超声速飞行器热防护系统等方面都有着重要的应用[1-3]。

由脆性基体和纤维组成的陶瓷基复合材料之所以能表现出非脆性断裂行为，是因为纤维与基体之间的界面起着决定性作用。界面相的性能决定了碳纤维与基体间相互作用的强弱和增韧效果的优劣：如果纤维与基体的界面结合强度太弱，难以实现力的传递；如果纤维与基体的界面结合强度太强，就达不到增韧效果。因此陶瓷基复合材料的界面有一个最佳强度[4]。国内外研究者对复合材料界面进行的研究主要包括两个方面：一是界面的微观结构和性质，如杨序纲等[5]利用拉曼光谱和扫描电镜对SiC纤维增强碳化硅、JG6玻璃和Pyrex玻璃复合材料界面的微观结构进行了研究；Manocha等[6]利用扫描电镜观察分析了不同热处理条件下C/C复合材料的微观结构。二是界面应力传递，如Mueller等[7]利用单纤维压出实验研究了界面的断裂韧性；Jäger J等[8]研究了复合材料塑性变形对纤维压出实验的影响；Hannes Kessler等[9]对微滴包埋拉出实验进行了研究。由于界面结构尺寸微小，分析复杂，实验研究难度很大，近年来许多研究者开始采用有限元仿真方法结合实验对复合材料界面进行研究，如Wei Y等[10]提出了一种界面层过渡模型；陶永强等[11]采用剪滞分析理论预测了二维编织陶瓷基复合材料在双向等轴拉伸载荷下的应力-应变关系；Mi Y等[12]提出了内聚力模型；Zhang等[13]等利用内聚力模型模拟界面进行了复合材料的渐进损伤分析；Bienias等[14]利用XFEM方法研究了纵向拉伸CFRP过程中的断裂行为；Liu C等[15]、寇剑锋等[16]研究了内聚力单元的参数；张立峰[17-18]、李巾锭等[19]进行了C/SiC复合材料单纤维压出实验及有限元仿真研究。

本研究采用内聚力模型模拟C/SiC纤维/基体界面，通过有限元仿真模拟了三点弯曲模式下界面的脱粘过程，并研究了纤维方向、界面厚度对三点弯曲过程中界面强度的影响规律。

2 有限元模型的建立

2.1 PyC(热解碳)界面本构模型

界面的本构模型选用Mi Y等[12]提出的双线性本构模型(Bilinear Traction Separation Law)，其中牵引力是脱粘位移的函数，其先随着脱粘位移增大而增加，当牵引力达到强度失效准则时，内聚力单元进入损伤失效模式即刚度弱化形式，随着内聚力单元分离的继续进行牵引力将逐渐减小至零，此时内聚力单元完全失效，内聚应力-分离位移关系如图1所示。曲线峰值应力，即分离强度；曲线与横轴包围面积，即断裂能。

本构关系见下式：

图1 张力-位移关系曲线图Fig.1 Traction-separation curve

式中，损伤变量d从0到1单调增加，d=0代表未损伤，d=1则代表完全破坏。

损伤变量d的表达式为：

式中：δm为加载过程中的最大等效位移，分别为材料初始损伤和完全失效时的等效位移。

初始损伤判据采用最大主应力准则MAXS，见式(3)。当应力达到最大应力值(图1中三角形的高)时单元承载能力下降，损伤开始：

随着损伤演化当超过界面临界断裂能时单元完全破坏，见式(4)：

2.2 几何建模

单向C/SiC复合材料扫描电镜放大5000倍后的图像见图2。当纤维方向垂直于基体与负载方向构成的平面时称为横向(Transverse)，如图2(a)所示；当纤维方向平行于负载方向时称为法向(Normal)，如图2(b)所示。对复合材料的研究可采用多尺度建模，研究复合材料整体性能常采用宏观建模方式，研究界面强度一般需建立微米级的模型。图3是根据图2电镜所示复合材料的微观结构和文献[17]，用ABAQUS软件构造微观有限元模型，该模型的建模尺度与实际微观模型近似一致，模型尺寸单位为μm，其它单位进行相应换算。由于实际的压头、支架尺寸远大于纤维和界面的尺寸，为了模拟在微观情况下的三点弯曲实验，采用对材料施加弯矩的方法。

图2 单向C/SiC复合材料显微形貌图Fig.2 SEM images of the C/SiC composites

图3 ABAQUS中的复合材料微观模型Fig.3 Composite microstructure in ABAQUS

在本模型中，纤维和基体选用结构化网格划分，单元类型为CPS4R；在PyC界面处进行适当的网格细化，并选用扫掠网格划分，采用内聚力单元(cohesive)，类型为COH2D4。材料属性见表1和表2[20，21]。

表1 SiC基体和C纤维的材料属性Table 1 Material properties of SiC and carbon fiber

表2 PyC界面的材料属性Table 2 Material properties of PyC

3 结果与讨论

3.1 仿真结果与实验结果对比

三点弯曲实验如图4所示进行，实验采用型号为CSS-44001型的电子万能试验机，工件由山东工程陶瓷研究院采用CVI工艺制作，通过控制温度和压力使PyC(热解碳)界面厚度为0.2μm。纤维体积分数为40%，尺寸为60×5×3mm，跨距为40mm，纤维方向为横向，采用位移加载。

将实验得到的结果转化为应力-应变曲线并与仿真得到的结果进行对比，如图5所示。

仿真得到的纤维方向为横向时的界面强度为28.3MPa，略大于实验得到的结果，仿真结果与实验结果误差最大约为7.6%，原因可能是材料沉积过程并不能达到非常好的致密度(见图2)，复合材料中存在孔隙导致强度变小。

图4 三点弯曲实验图Fig.4 Three point bending test

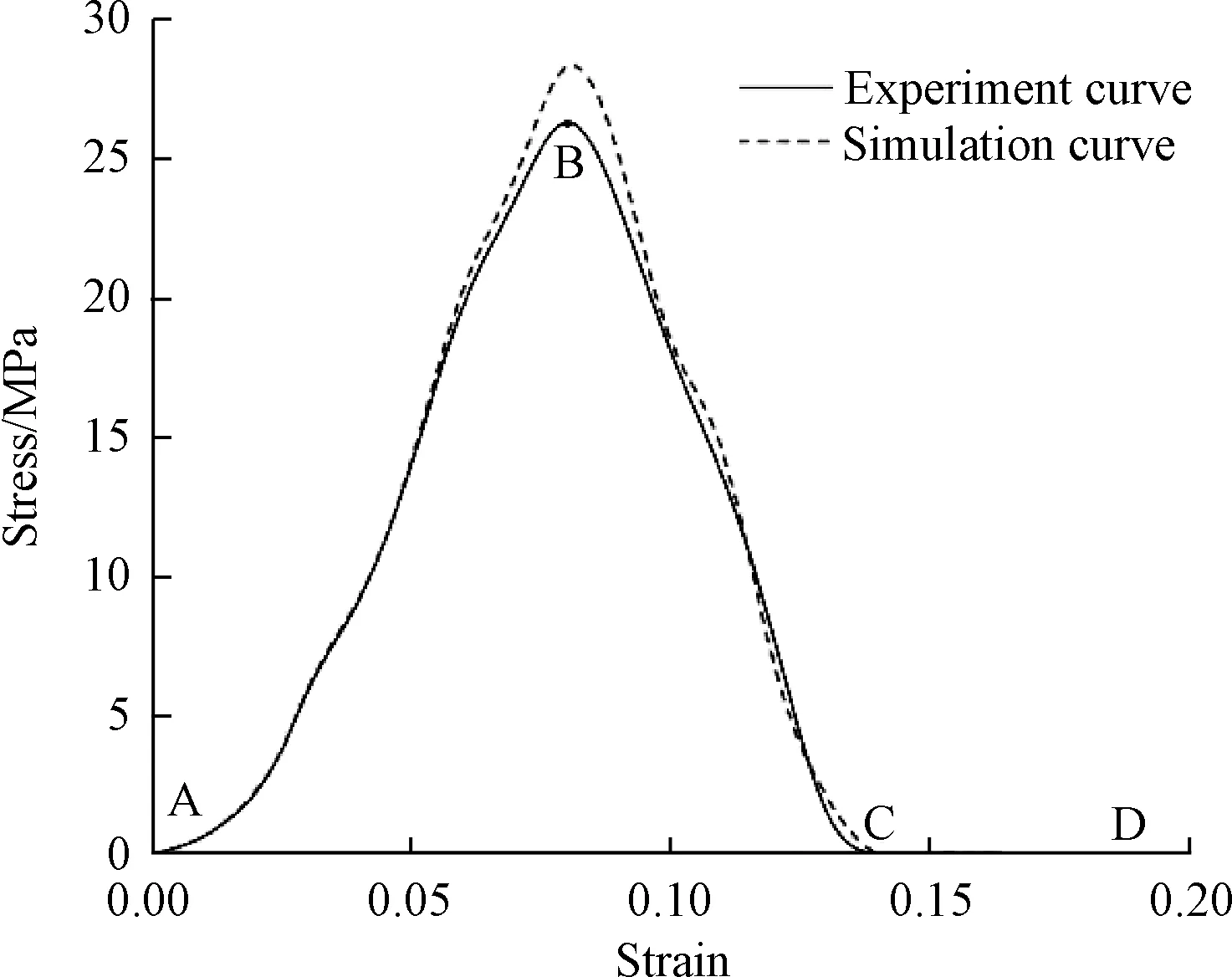
图5 仿真结果与实验结果的应力-应变曲线对比图Fig.5 Comparison of stress-strain curves between simulation and experiment

3.2 PyC(热解碳)界面脱粘过程模拟

根据实验所测得的界面处的应力应变行为以及许多复合材料研究者的研究结果表明，复合材料界面的刚度跟单一材料有很大的区别，它随着纤维和基体由结合到分离的过程而发生变化。本研究采用双线性内聚力模型来模拟界面进行仿真得到了与实验较吻合的结果。对复合材料施加与实验相同的弯矩，随着界面位移的增加，界面发生刚度退化和脱粘，纤维方向为横向和法向时C/SiC复合材料界面的变形过程基本相同，对应于图6，7中的三个阶段。

在图6，7中：(a)～(b)为线弹性阶段：此阶段应力应变呈线性关系，界面刚度不变(即图5中的曲线上升阶段)。(b)～(c)为刚度退化阶段：当应力达到最大值时，界面开始损伤，刚度变小(即图5曲线最高点和下降阶段)。(c)～(d)为界面脱粘阶段：此时界面应变达到最大，界面完全破坏，纤维与基体分离。

3.3 不同纤维方向下的PyC(热解碳)界面脱粘强度

纤维方向为横向和法向时的应力-应变曲线如图8所示，曲线峰值即为对应的界面脱粘强度。仿真得到的纤维方向为横向和法向时的界面脱粘强度分别为28.3及27.8MPa，从图可见，纤维方向横向或法向对界面脱粘强度影响不大。

图6 纤维方向为横向时的应力云图Fig.6 Stress nephogram of transverse fiber direction

图8 不同纤维方向的应力-应变曲线Fig.8 Stress-time curves of different fiber orientations

3.4 不同界面厚度下的PyC(热解碳)界面脱粘强度

ABAQUS在cohesive建模中使用了很“人性化”的设计，实际问题中界面可能很薄或者需要改变界面厚度时，可以通过定义cohesive section中的厚度来改变界面厚度，而不用重新建模。在纤维方向为横向和法向时，不同界面厚度下的界面脱粘强度如图9所示，界面脱粘强度随界面厚度增大而增大，当界面厚度约为0.2～0.3μm时，界面脱粘强度达到最大，此时再增大界面厚度并不能明显增大甚至会减小界面的脱粘强度。

图7 纤维方向为法向时的应力云图Fig.7 Stress nephogram of normal fiber direction

图9 界面脱粘强度随界面厚度的变化曲线Fig.9 Variation of interfacial debonding stress with coating thickness

4 结 论

1.利用ABAQUS软件对C/SiC复合材料弯曲过程的研究是可行的。仿真得出的纤维方向为横向和法向时的界面脱粘强度大致相等，约为26～28MPa。

2.PyC(热解碳)界面脱粘强度随着界面厚度的增大而增大，当界面厚度约为0.2～0.3μm时，界面脱粘强度达到最大，此时再增大界面厚度并不能明显地增大甚至会减小界面的脱粘强度。

3.仿真结果与试验对比表明，内聚力模型用于表征C/SiC复合材料的界面比较合理。