基于卷积神经网络算法的自动地层对比实验

徐朝晖，刘钰铭，周新茂，何辉，张波，吴昊，高建

1 中国石油大学(北京)地球科学学院 北京 102249

2 中国石油勘探开发研究院 北京 100083

3 阿拉巴马大学地球科学系 塔斯卡卢萨 美国 35487

0 引言

油气藏内井间地层对比是油藏描述与储层表征的关键步骤之一，对比结果直接决定油藏格架并进一步控制了油藏内储集体的空间分布，最终影响油气藏的开发[1]。地层对比的核心工作主要由地质工作者依据标志层、沉积旋回和岩性组合等测井曲线特征，通过建立覆盖全油田所有井的相互交叉的连井剖面完成[2]。然而，油田进入开发中后期钻井增多，地层对比工作量十分繁重。目前，已有商业软件辅助地层对比工作，但其主要贡献限于井数据库和对比剖面的建立，而对于单井地层划分和连井剖面上井间地层对应关系分析这一核心工作，主要通过地质工作者眼、手、脑并用进行综合分析完成。其不足在于：一是带来眼力、体力和脑力上的极大耗费；二是主观性强，对比结果高度依赖于地质工作者个人的相关知识和经验。近年来，有学者采用模糊数学[3]、层内差异与聚类分析法[4]、沃尔什变换[5]、测井信号相似性对比[6]以及神经网络[7]等方法尝试实现自动地层对比，但并未取得明显的可应用于工业实践的成功。地层对比不仅仅是测井曲线形态的对比，本质是测井曲线所隐含的地质信息的对比，而许多地质信息(如多级沉积旋回)往往比较抽象难于用数学语言来表达。

当前，人工智能(Arti ficial Intelligence，简称AI)的浪潮正在席卷全球，深度学习(Deep Learning，简称DL)方法是推动这一轮浪潮的核心力量[8]。深度学习善于从原始输入数据中挖掘抽象的特征表示，而这些表示具有良好的泛化能力[9]。卷积神经网络(Convolutional Neural Networks，简称CNN)是以卷积为计算核心且具有深度结构的前馈神经网络，是深度学习的代表算法之一，因其强大的特征学习与分类能力在图像分类[10]、目标检测[11]、图像语义分割[12]等领域取得了一系列突破性的成功，其原理与人工地层对比中对测井曲线进行特征提取与分析有相通之处。本文采用卷积神经网络算法，开展自动地层对比实验研究，以探索人工智能在油气地质研究中的效果。

1 实验工区

实验工区选择大庆油田喇嘛甸油田，构造位置位于松辽盆地大庆长垣北端(图1)，已开发四十多年，先后部署了基础井网、一次加密、二次加密等多套井网，钻井、测井资料齐全。对比目标井段属于中白垩统嫩江组，沉积环境为大型河流三角洲前缘，主要发育分流河道砂体[13]。储层岩石类型以细砂岩、粉砂岩和泥岩为主，纵向上整体表现为“泥包砂”特征。选取地层对比井段为某含油层系(记为S)，地层厚度约200 m，进一步划分为4个油层组(如S1)、10个砂层组(如S11)、30个小层(如S111)。其中，单一油层组厚度25～50 m，单一砂层组厚度10～20 m，单一小层厚度 5～10 m。

图1 区域沉积背景及研究区位置图Fig.1 Sedimentary background and location of study area

在喇嘛甸油田内部选取长9 km、宽5 km的实验区(图2)，该区内未发育断层，表现为大型背斜，构造相对简单。以实验区内分布较为规则的基础井网和一次加密井为实验对象井，总井数463口(图2)，并将这些井重命名为W1、W2、……、W463。实验对象井均完钻于1970年代，其分层数据历经四十多年开发实践的检验，具有较高的可靠性。

实验对象井测井资料齐全。基于“岩心刻度测井”方法，选择对岩性敏感的自然电位曲线(SP)和微电极曲线(ML1、ML2)作为地层对比基准曲线(图3)。

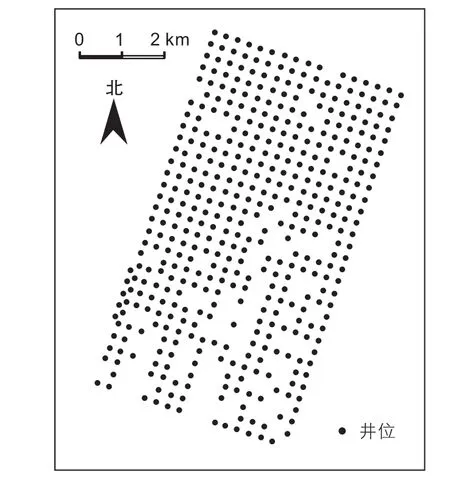
图2 研究区实验井位图Fig. 2 Well locations for automatic stratigraphic correlation experiments

图3 过W1-W2-W3井地层对比剖面示意图Fig. 3 Sketch of stratigraphic correlation pro file through well W1, W2 and W3

2 实验原理

2.1 卷积神经网络的基本原理

1989年，LeCun等人在论述神经网络的网格结构时首次提出了“卷积”一词[14]，标志着“卷积神经网络”的诞生，LeNet是一种多阶段全局可训练的人工神经网络模型，可以从经过简单预处理的、甚至原始的数据中学习到抽象的、本质的和高阶的特征。2006年，Hinton提出了深度学习的概念[15]，基于深度神经网络在大量的数据中自动提取、学习高层特征。

卷积神经网络是一种具有深度结构的前馈神经网络，具有局部感知、权值共享、降采样的特点。典型的卷积神经网络结构包括输入层、卷积层、池化层、全连接层和输出层(图4)。卷积层的本质是特征提取，如同模仿眼睛扫描物体进行图像特征提取的过程；池化层，即降采样层，实现特征数据的降维处理，在减少数据同时保留有效信息，如同闭上眼睛回忆看到的事物的最重要的特征，是压缩图像并保留重要信息的过程。全连接层位于网络模型末端，用于对各卷积和池化层特征的回归、分类等处理，并汇总为特征向量。

图4 卷积神经网络模型的基本结构Fig. 4 Structure of convolutional neural networks model

图5 SegNet网络结构示意图Fig. 5 Schematic diagram of SegNet model

2.2 卷积神经网络模型及参数选择

随着深度学习理论的不断完善，卷积神经网络引入了多类学习和优化理论，在结构上不断加深，先后提出了多种算法。SegNet模型是一种应用于像素级别的图像分割任务的卷积神经网络模型[16]。地质研究中，地层划分与对比可看作为一种图像分割任务，故本实验选用SegNet网络模型对地层进行自动划分。

SegNet网络模型由Badrinarayanan于2016年提出，该网络通过端到端的方式实现目标体的分类。SegNet网络结构包括编码网络和解码网络两部分(图5)。编码网络主要由一系列基于非线性处理的层组构成，每个层组由卷积层、分批归一化层、激励函数层和最大池化层组成，主要通过卷积对输入数据图像的特征信息进行提取，并通过池化操作不断缩小输入数据规模。解码是编码的反过程，同样由一系列基于非线性处理的层组构成，每个层组由上采样层、卷积层、分批归一化层、激励函数层组成，主要目的是对输入数据进行上采样，还原原始输入数据图像。网络结构参数选择是保证试验效果的关键。根据SegNet网络相关原理，结合地层划分中的地质特点分析认为，影响实验效果的主要参数为非线性处理层组的数量选择、卷积核大小、卷积核数量等。

非线性处理层组的数量取决于处理井段的厚度和采样点数据量。在编码网络中，每经过一非线性层组，数据都会减半；而在解码网络中，每经过一非线性层组，数据大小都会翻倍。根据参数调整经验，编码网络中最后的非线性层组的数据量大小为地质层位数量(在输入数据中为标记类别数量)的1到2倍时效果最好。假设平均厚度为20 m的一套地层，按照测井系列数据8点/m得采样频率，则其数据大小为160×1；按照油组级别地层单元，标记类别数量为4；此时设计10组非线性处理层组(编码网络5组，解码网络5组)，则第一非线性层组输出数据大小为80×1，而第二非线性层组输出数据大小为40×1，依次类推，至第五组非线性处理层组时输出数据量大小为5×1。实验分析表明，此时网络训练效果会比较好。

卷积核均为n×1数组，其数量和大小根据参数调整的经验确定。在编码网络中，第一层卷积核大小为50×1，自第二层开始依次减小，最后一层卷积核大小降为3×1；卷积核数量上，各非线性层组并不相同，一般后面层组的数量大于或等于前一层组数量，如第一层组为64个，后面层组可依次增大为128个、256个、512个等。在解码网络中，每层的卷积核大小和数量变化趋势与编码网络中各层相反。

2.3 自动地层对比思路

人工在连井剖面上进行地层对比时，往往要先通过大量的观察在测井曲线上找出标志层、沉积旋回等可用于对比的地质信息，然后利用这些信息连接井间地层。而对于卷积神经网络而言，在研究过程无法像决策树、回归等传统的机器学习算法一样，确定每一非线性层组的具体物理意义。根据卷积神经网络算法原理，自动地层对比实验分“训练和预测”两大部分(图 6)。

图6 基于卷积神经网络的自动地层对比试验设计思路Fig. 6 Flow chart of automatic stratigraphic correlation using convolutional neural networks

第一部分，训练。针对选定的已知分层的井，将测井曲线作为数据输入(Data)，以各井对应的单个地层单元的分层数据为标注(Label)，通过SegNet网络算法，自动提取各地层单元的特征信息，并建立卷积模型。本次研究，我们选择了自然电位(SP)、微电极(ML1、ML2) 3条测井曲线。输入数据文件4个，其中3个Data文件、1个Label文件。Data文件分别代表三条曲线，每个文件为n×1数据，其中n代表了测井数据的数据量。Label文件为确定的地层分层数据文件，代表了现有的分层结果，用于样本学习。

第二部分，预测。针对未知分层的井，将测井曲线(Data)作为数据输入，基于训练建立的卷积神经网络模型，开展测井曲线图像的分割分类，匹配到可能性最高的地层单元，从而实现地层自动划分。

3 实验方案设计

表1 实验井数和比例Table 1 Number and proportion for experimental well

图7 训练井与预测井平面分布Fig. 7 Well location map for training and testing

实验中，随机选取部分实验对象井作为训练样本，对未参与训练的实验对象井进行自动地层对比预测，并与原始分层数据比对进行误差分析。按照训练样本的实验对象井数据比例65%、40%、20%和10%将实验分为a)、b)、c)、d)共4组(表1)。作为训练样本的实验对象井随机抽取，其平面分布如图7所示。

为揭示实验效果，每组实验针对油层组、砂层组和小层三个级次地层单元进一步设置3个相互独立的实验，即实验为4组，每组3个，共12个。

4 实验结果

4.1 单井预测准确度

将单井全井段预测的结果与原始分层数据进行比对，并计算准确度。单井预测准确度Aw定义为

公式(1)中，预测正确的点数，是指就测井曲线上每个点而言，若预测的地层归属与原有分层数据一致，则该点计为预测正确的点。可以看出，单井预测准确度也可以理解为预测结果与原有分层结果一致的厚度与总厚度的百分比。以W345井砂组级地层单元预测为例(图8)，其在训练井数为65%、40%、20%和10%等4组实验中预测准确度分别为98.3%、98%、97.7%和92.5%。

分别计算了12个实验所有井预测结果的准确度，采用算术平均方法求取每个实验的平均单井准确度(表2)。整体上，对于就某一特定的地层级别而言(比如砂组)，单井准确度随训练量降低而降低；就某特定的训练量而言(比如40%)，单井准确度随地层单元细分而降低。具体地说，在训练量大于等于20%时，油组和砂组级别的单井预测准确度，都超过了90%，说明只需要20%的已知分层数据就可以较为可靠进行砂组和油组级别的自动地层对比。对于小层级别的地层单元而言，当训练量小于等于40%时，其预测准确度都低于70%，说明小层级别的自动对比需要较多的训练数据。

图8 WA井砂组单元预测结果与原始分层对比示意图Fig. 8 Correlation of original and predicted Stratigraphic unit for well WA

4.2 单一地层单元预测准确度

对于某一级次的单一地层单元而言，其预测准确度As定义为：

公式(2)中，单井上，某特定地层单元预测是否正确取决于该地层单元顶面、底面与原始分层数据的决定，若顶、底面绝对误差之和不超过2 m，则认为该井预测结果准确；反之，则不准确。之所以把可容忍的最大误差定为2 m，是因为该区单个有效砂体的厚度往往都大于2 m，即正确的预测结果不会改变2 m以上砂体对应的地层单元归属。

统计发现，油组级别的单层预测准确度在训练量为65%、40%、20%和10%时均大于等于90%(图9)，说明只需要10%的训练量就可以对油组级地层单元进行可靠预测。

表2 自动对比实验平均单井预测准确度统计表Table 2 Average prediction accuracy of single well for automatic stratigraphic correlation

图9 油组级地层单元单层预测准确度Fig. 9 Prediction accuracy of stratigraphic units for formation level

砂组级别的单层预测准确度随预测量的降低依次降低，训练量为65%时砂组级单层预测准确度不小于90%；训练量为40%时砂组级单层预测准确度在82%～97%，10个地层单元中有5个准确度不小于90%；训练量为20%时砂组级单层预测准确度在75%～95%，10个地层单元中有4个准确度大于90%，有1个小于80%；而训练量为10%时砂组级单层预测准确度在44%～94%，10个地层单元中有3个准确度大于90%，有2个小于60%(图10)。

图10 砂组级地层单元单层预测准确度Fig. 10 Prediction accuracy of stratigraphic units for sand group level

小层级别的单层预测准确度随预测量的降低依次降低，训练量为65%时，30个小层中11个准确度大于90%，14个在80%～90%，5个小于80%；当训练量为40%时，30个小层中有17个小层准确度小于80%；当训练量为20%和10%时，准确度进一步降低(图11)。

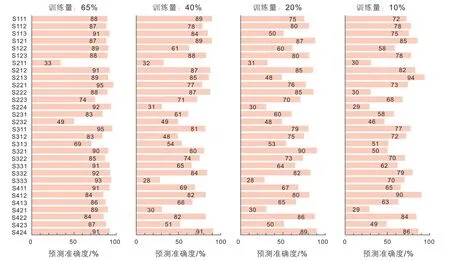
图11 小层级地层单元单层预测准确度Fig. 11 Prediction accuracy of stratigraphic units for single layer level

此外，相对于油组与砂组而言，小层级别的单层预测准确度的层间差异较大，进一步分析发现该差异与小层砂体平面分布相关。如图12所示，砂体或非储层分布较为均匀的S121、S424小层其准确度较高，而砂体和非储层分布相对不均匀的S211小层其准确度较低。

图12 小层砂体厚度平面图Fig. 12 Sketch maps of sand thickness for single layer

5 结论与展望

5.1 结论

(1)训练量越大，自动对比效果越好；地层级别越高(厚度越厚)，自动对比效果越好。

(2)对于砂组及以上级别地层单元而言(厚度不小于10 m)，20%的训练量就可以较为可靠地进行自动地层对比。说明卷积神经网络算法能有效应用于依据测井曲线图像进行油藏规模地层自动对比，具有良好的发展前景。

5.2 展望

目前，尚未见有采用人工智能方法进行地层自动对比的研究报道。本文提出的采用卷积神经网络进行自动地层对比的探索性实验表明，该方法对于构造简单、测井响应特征明显的砂泥岩储层适用性好，自动地层对比结果能够满足生产实践需要。然而，深度学习算法对于复杂储层的自动地层对比的适用性和效果有待进一步落实。为进一步提高自动地层对比效果，应基于实际的地质规律进一步改进算法：

(1)地层单元在垂向上有分级控制的旋回性，采用预测准确度更好的高级次(如砂组)对比结果约束进行低级次(如小层)地层对比，可进一步提高低级次地层对比的准确性。

(2)本次实验中用于训练的井和用于预测的井在平面上是随机选取的，若能在预测时考虑训练的井与预测的井的空间关系，并结合沉积物源等地质信息对预测过程进行干预，可能会提高预测准确度。

(3)本次实验未考虑地层对比中较为常见的断点问题，下一步可结合地震解释或断层信息，在预测过程中考虑各井的空间位置，实现断点自动对比。