核心素养立意是高考数学命题的基本原则

□赵思林柴文斌胡富雅

（1.内江师范学院数学与信息科学学院，四川内江 641112；2.四川省遂宁中学，四川遂宁 629000）

40多年来，我国高考数学命题的立意经历了从“知识立意”到“能力立意”，再到“数学核心素养立意”的发展与转变.以数学核心素养立意的高考命题，就是首先确定试题在数学核心素养和能力方面的考查目的，然后根据核心素养和能力考查的要求，选择适当的知识和技能，设计恰当的情境和问题．以“核心素养立意”的试题一般不会只考查某一个核心素养，比如考数学抽象素养，那么命题的一般思路是以考查数学抽象为主，兼考其他一个或多个核心素养.分析2018年高考数学全国卷发现，很多题目同时考查六个核心素养中的几个素养，单独只考某一个核心素养的题目比较少.下面从六个核心素养的角度，对2018年高考数学全国卷部分试题的立意作分析和点评．

一、以数学抽象立意

高度的抽象性是数学的基本特征．数学基本概念的形成、公理体系的建立等都必须经历抽象的过程．数学抽象在几何（如平面几何、立体几何等）、代数（如函数、不等式、排列组合等）、向量、导数中都有广泛的应用．数学抽象可以把具有生产生活背景的实际问题抽象为数学问题，并能够将实际问题用抽象的概念和符号表示成数学模型．因此，数学抽象素养是高考的重要考点．

例1（2018年全国卷Ⅱ理科11题）已知f(x)是定义域为(-∞,+ ∞)的奇函数，满足f(1-x)=f(1+x).若 f(1)=2，则 f(1)+f(2)+f(3)+…+f(50)=____．

A.-50 B.0 C.2 D.50

立意与分析1：本题考查抽象函数的奇偶性（对称性）、周期性、数列求和等知识，考查数学抽象、逻辑推理、数学运算、直观想象等核心素养 .由 f(1-x)=f(1+x)可知，函数f(x)的图象关于直线x=1对称，这里需要具有直观想象素养．又由f(x)是奇函数，可以推出函数f(x)是一个以4为周期的周期函数．

解法1：（略）．

立意与分析2：由立意与分析1知，函数f(x)是一个以4为周期的周期函数.本题也可以采用特殊值法，即把函数f(x)看成（当成）一个特殊的函数.怎样找到（或构造）这个特殊的函数呢？首先，注意到f(x)是周期函数，容易联想到三角函数；其次，由f(x)是定义域为(-∞,+ ∞)的奇函数，可联想到正弦型函数Asin(ωx+ φ)，由周期可取从而，这个正弦型函数可能是Asin(

π2x+ φ )；接着，注意到f(0)=0，因此可猜想这个正弦型函数可能是最后，由f(1)=2，可把f(x)看成到此，就构造出满足题设四个条件（定义域是(-∞,+ ∞)，奇函数，f(1-x)=f(1+x)及f(1)=2）的一个具体函数了，问题就容易解答．

解法2：（用特殊值法）构造易知h(x)满足题目的所有条件，因此可以取f(x)=h(x).计算得，h(1)=2,h(2)=0,h(3)=-2,h(4)=0．

所 以 f(1)+f(2)+f(3)+…+f(50)=12［f（1）+f（2）+f（3）+f（4）］+f（1）+f（2）=2.

故选C．

评注：本题以抽象函数为载体，以周期函数为背景，主要考查了数学抽象素养，也兼考逻辑推理、数学运算、直观想象等核心素养.具体地说，为考查数学抽象这一核心素养，题目设计了一个具有奇偶性、对称性、周期性等的抽象函数f(x).由于题目中的函数符号f(x)、函数方程f(1-x)=f(1+x)，以及求和形式f(1)+f(2)+f(3)+…+f(50)都具有抽象性，因此考生只有破解这些抽象性，才能得到答案.考生要想破解这些抽象性，可以考虑运用“形”的直观性，即是说，利用“f(x)是定义域为(-∞,+ ∞ )的奇函数”等价于“f(x)的图象关于坐标原点对称”，“f(1-x)=f(1+x)”等价于“函数f(x)的图象关于直线x=1对称”，通过画图不难发现f(x)是一个周期函数，并且一个周期为4.至此，问题的解答就容易了.对于数学抽象的考查一般有两种方式：一是考查对问题及在问题解决过程中需要运用的数学抽象的方法，如引入符号、把问题一般化等才能解决问题；二是考查对抽象的符号、抽象的函数、抽象的方程、抽象的代数式等的认识、处理和运用，特别应重视充分发掘抽象的数学结构的几何意义.特殊化、直观化、具体化等是解决数学抽象问题的基本思维策略与方法．

二、以逻辑推理立意

逻辑推理是数学根本特色.推理包括合情推理和逻辑推理.逻辑推理是数学思维的基本形式之一.逻辑推理是培养学生理性思维的基本策略和重要抓手.绝大多数高考数学试题都与逻辑推理有关，或能找到逻辑推理的影子．

例2（2018年全国卷Ⅲ理科16题）已知点M(-1,1)和抛物线C:y2=4x，过C的焦点且斜率为k的直线与C相交与A,B两点，若∠AMB=90°，则k=___．

立意与分析：本题考查斜率公式、直线方程和抛物线等基础知识，主要考查数学运算等核心素养.若用“算”的方法，需解消元，得k2x2-(4+2k2)x+k2=0，接着用韦达定理，并用直角坐标或向量法可以做下去，但计算过程较为烦琐.若用抛物线定义和平面几何知识，就可推出抛物线y2=2px(p＞0)的一个重要性质：以焦点弦AB为直径的圆与抛物线的准线相切，并且MF⊥AB.利用MF⊥AB，可大大减少运算量，达到多想少算的目的．

解：设点A,B在准线上的射影点分别为A1,B1，弦AB的中点为K，则AA1B1B为直角梯形（图略）.显然，点M在准线x=-1上．

又因为∠AMK=90°，

因此，MK是直角梯形AA1B1B的中位线．

所以，点M为A1B1的中点，且MK//AA1．

所以，∠MAA1=∠AMK．

又由MK=AK，知∠AMK=∠MAK．

所以∠MAA1=∠MAF．

因此△MAA1≌△MAF（“边角边”）．

从而可得，MF⊥AB．

评注：本题立意是考查解析几何基本思想方法，即以解析几何知识为载体考查数学运算等核心素养.解析几何的基本思想方法是用代数方法研究几何问题，就是以“算”为主，这当然是通性通法.但对本题而言，这并不是最佳方法.若用抛物线定义和平面几何知识，就可演绎推出MF⊥AB，这样就可以极大地减少运算量，享受“多想少算”的乐趣.本题作为填空题，只要画一个草图，上述逻辑推理的每一步的结论都可以在草图上直观地看出来（并不需要一步一步写出来），这需要考生具备直观想象素养．

三、以数学建模立意

数学建模肩负培养和考查学生数学应用意识的重任．修订后的高中新课标在高考和学业水平考试建议中，要求应有一定数量的应用问题，重点考查学生的思维过程、实践能力和创新意识，问题情境的设计应自然、合理．因此，考查应用意识或考查数学建模是一条长期坚持的命题原则．

例3（2018年全国卷Ⅱ理科18题）下图是某地区2000年至2016年环境基础设施投资额y（单位：亿元）的折线图.为了预测该地区2018年的环境基础设施投资额，建立y与时间变量t的两个线性回归模型.根据2000年至2016年的数据（时间变量t的值依次为1,2,…,17）建立模型①：ŷ=-30.4+13.5t；根据2010年至2016年的数据（时间变量t的值依次为1,2,…,7）建立模型②：ŷ=99+17.5t．

（1）分别利用这两个模型，求该地区2018年的环境基础设施投资额的预测值；

（2）你认为用哪个模型得到的预测值更可靠？并说明理由．

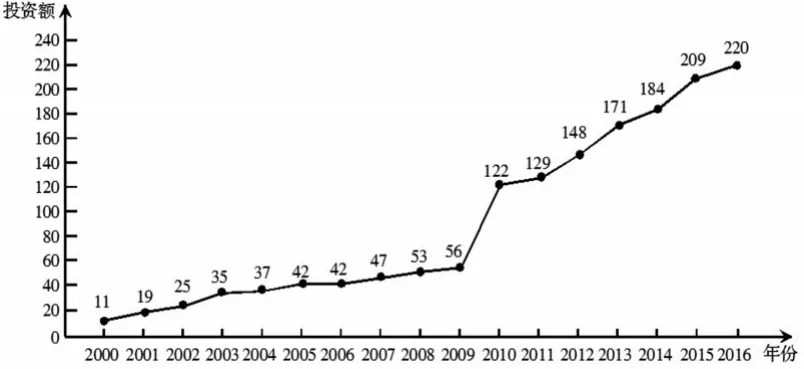
立意与分析：本题考查概率统计中的线性回归模型、折线统计图等基础知识，考查数据分析、数学运算、统计评价等数学素养.由已知数据来预测未来的数据，要求考生具有一定的数据分析能力．

简解：（1）模型①：当 t=19 时，ŷ=226.1（亿元）．

模型②：当t=9时，ŷ=256.5（亿元）．

（2）利用模型②得到的预测值更可靠．其理由是不唯一的，从略．

评注：本题属于“给定数学模型”的问题．第（1）问较简单，只要不把t的值取错，且运算能力过关，就不会有什么困难.第（2）问有几大亮点：一是考查了考生的预测能力，预测能力是杰出人物的重要心理品格.有格言说“预则立，不预则废”，这里的“预”是预测的意思，预测是对事物未来发展（趋势）的提前把握，概率统计具有预测功能.二是考查统计评价，体现统计的预测功能和实用价值.三是通过本题考查考生的高级认知能力，从认知的角度看，评价属于高层次、高水平的认知能力.通过概率统计的学习培养学生高层次认知能力，是一条非常有效的教学策略.四是考查考生的书面表达能力.五是第（2）问是一个（结论）开放性问题，这是因为第（2）问的理由的说明方法不唯一，属于结论开放性问题．开放性问题是高中新课改和教育部考试中心大力倡导的，应予重视．

四、以直观想象立意

想象是人类大脑最奇妙的现象之一.想象是人类进行创造性思维活动最基本的思维方式.直观想象是指借助于图形（图象）、表格、模型等数学直观性材料而产生的想象.直观想象包括利用图形描述、立意与分析数学问题等.想象包括直观想象和非直观想象.立体几何承担着培养和考查空间想象能力的重任.在学习立体几何时，看图、画图、判图（判断图形）、想图（想象图形）、用图（应用图形）、构图（构造图形）等是培养空间想象素养的有效方法.数形结合是训练直观想象有效的途径．在教学中，不能只重视通过几何的学习来培养直观想象素养．教师也应适当关注非直观的想象的培养，让学生把不直观的数学对象想象成直观的对象，把直观的数学对象想象成不直观的对象，这需要非凡的想象力．

例4（2018年全国Ⅰ卷理科12题）已知正方体的棱长为1，每条棱所在直线与平面α所成的角相等，则α截此正方体所得截面面积的最大值为（ ）．

立意与分析：本题以正方体为立体模型，考查了直线与平面所成的角的概念、多面体的截面、多边形的面积等知识，考查了直观想象、逻辑推理、数学运算等核心素养.先考虑把正方体切去一个大角（就是把同一顶点所引的三条棱全部都切掉），切去的这个大角上的三条棱所在直线与这个截面所成的角都相等，由此推出，切去大角的截面与正方体的每条棱所在直线所成的角都相等.再由正方体的对称性，找出与此截面平行且全等的另一个截面，则最大截面应位于这两个平行截面的正中间，如图所示．

解：（略）．

五、以数学运算立意

数学运算体现“量化”的数学观，是数学重要的基本素养之一.运算能力是高考考查的重点之一，大部分题目对运算能力都有一些要求.数学运算一般是逻辑推理、数学建模和数据分析的基础性素养.数学是需要算的，但并不提倡硬算、蛮算、繁算，而是提倡“算”“想”结合，多想少算．

例5（2018年全国卷Ⅲ理科12题）设a=log0.20.3，b=log20.3，则（ ）．

A.a+b＜ab＜0 B.ab＜a+b＜0

C.a+b＜0＜ab D.ab＜0＜a+b

立意与分析：本题考查对数的运算、对数函数的性质和不等式的性质，主要考查数学运算等核心素养.题目中两个对数式的真数相同，以及各选项中都含有a+b,ab结构，因此考虑把a+b,ab化成含有的形式.不难得到即可获解．

解：观察发现：题目中两个对数式的真数相同，考虑到对数的底数相同时才便于运算，换底得再注意到各选项都含有a+b,ab结构，因此可考虑把a+b,ab化成含有的形式.易知log0.30.2+log0.32=log0.30.4＞1.又因为 a＞0,b＜0，所以ab＜0,a+b＜0，因此ab＜a+b＜0，故选B．

评注：本题明显有考查运算能力的意图，然而直接计算或估算都比较麻烦.观察到a,b的特点即a,b的真数相同但底数不同，底数不同不便于对数的运算，因此考虑运用换底公式把a,b分别变成的形式.从上面的解答可以看出，本题并不是直接要求考生对a+b,ab进行计算（或估算），而是希望考生设计或挑选出简便的算法，要设计或挑选出简便的算法就必须弄懂算理．

六、以数据分析立意

数据分析是指能够从题目数据中提取关键信息，对已知数据进行细致的分析，从而建立相应的模型，进而解决问题．数据分析离不开逻辑推理和数学运算这两大核心素养．

例6（2018年全国卷Ⅲ理科18题）某工厂为提高生产效率，开展技术创新活动，提出完成某项生产任务的两种新的生产方式．为比较两种生产方式的效率，选取40名工人，将他们随机分成两组，每组20人，第一组工人用第一种生产方式，第二组工人用第二种生产方式．根据工人完成生产任务的工作时间（单位：min）绘制了如下茎叶图：

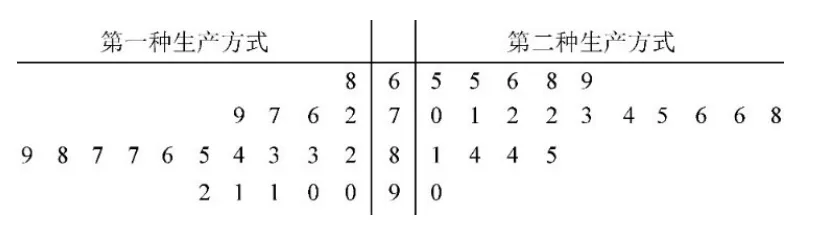
（1）根据茎叶图判断哪种生产方式的效率更高，并说明理由；

（2）求40名工人完成生产任务所需时间的中位数m，并将完成生产任务所需时间超过m和不超过m的工人数填入下面的列联表：

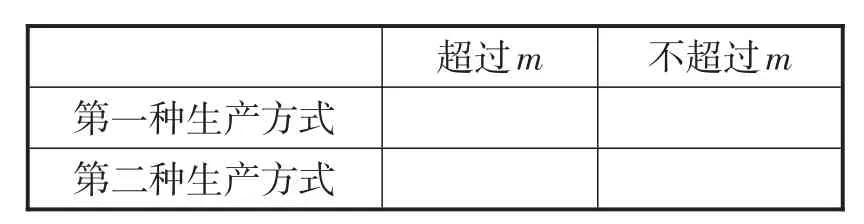
第一种生产方式第二种生产方式超过m 不超过m

（3）根据（2）中的列联表，能否有99%的把握认为两种生产方式的效率有差异？

P(k2≥k)k 0.050 3.841 0.010 6.635 0.001 10.828

立意与分析：本题以“技术创新”为背景，设置一个接近真实的问题情境，考查茎叶图、独立性检验等基础知识，考查考生运用概率统计知识分析和解决实际问题的能力，考查数据分析、数学运算、统计评价等数学素养．第（1）问可以根据茎叶图的数据特征分析如计算两种生产方式的平均时间.第（2）问只需计算出中位数，再根据中位数补全列联表．第（3）问利用k2直接判断．

第（3）问则根据已给的公式计算出k2，再与已给表k进行比较可得结果．

简解：（1）第二种生产方式的效率更高．理由的答案不唯一，从略．

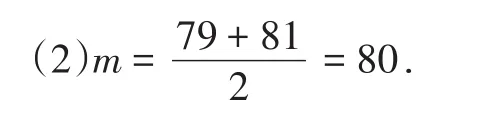
列联表如下：

第一种生产方式第二种生产方式超过m 15 5不超过m 5 15

评注：第（1）（2）问需要经历数据统计、整理、计算的统计过程.第（1）问得到结论是不难的，但其理由的回答不唯一，具有开放性，故此题属于（结论）开放性问题.第（2）问计算中位数m和填表都较容易.第（3）问的运算量不大.第（1）（3）问涉及统计评价．

总之，核心素养立意是高考数学命题的基本原则．高考设计试题一般以某个核心素养为主，兼考其他一个或多个核心素养.即是说，高考命题重视六个核心素养的综合性、交汇性．