数学运算素养下的一题多解

□王淼生 黄 勇

（厦门第一中学，福建厦门 361003；福建教育学院数学研修部，福建福州 350025）

一、数学运算

核心素养是我国新一轮课程改革的主要方向，体现高中课程的总体目标，标志着我国基础教育进入以培养核心素养为中心的新阶段．数学核心素养是未来合格公民应具备的最基本、最重要的学科素养.基于数学学科特点，《普通高中数学课程标准（2017年版）》首次明确提出数学抽象、逻辑推理、数学建模、数学运算、直观想象和数据分析等六大数学核心素养，其中数学运算历来是课程和教学的重点内容．数学运算是指依据运算法则，对数字、式子和量等运算对象进行代换或变换，强调解决问题的过程．数学运算并不仅仅是指数学计算，也不能理解为一般意义上的数学计算．数学运算不仅包括数字的简单计算，还包括各种数学式子及方程的变形，以及极限、微积分、逻辑代数的运算等.因此数学运算的核心就是理解运算对象、掌握运算法则、探究运算方向、选择运算方法、设计运算程序、求得运算结果.下面以一道题的一题多解为例，阐述数学运算素养的培养.

二、题目呈现

如图1所示，AB是半圆O：x2+y2=1（y≥ 0）的直径，点C为半圆上任意一点，延长AC到点P，使得CP=CB．

当点C从点B运动到点A时，动点P的轨迹的长度是（ ）．

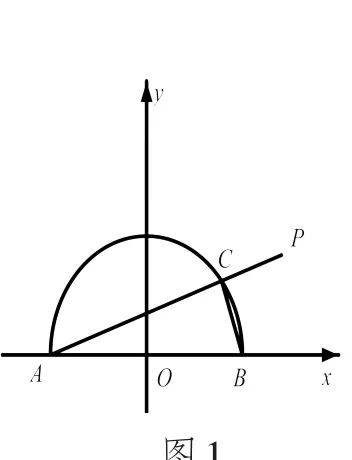
图1

三、题目分析

（一）运算对象

理解运算对象是实施数学运算的前提，否则数学运算就成为无源之水、无本之木.例题涉及解析几何中的直线、圆及它们之间的位置关系；涉及直线的方程、倾斜角、斜率；涉及平面几何中的圆、等腰三角形、直角三角形相关性质；涉及动点轨迹及弧长等运算对象．

（二）运算法则

掌握运算法则是实施数学运算的基础．对于直线与圆相交可以联立并解方程组，或运用韦达定理，或借助点到直线的距离公式；对于斜率可以利用k=tanα，也可以利用点的坐标来表示；对于几何问题，可以借助平面几何中的性质、定理（如三角形全等、相似）来处理．

（三）运算方向

实施数学运算关键在于探究运算方向，只有方向明确，才能保证运算在正确的轨道上运行.厘清问题本质是探究运算方向的基石.例题本质就是求满足条件的动点轨迹，主要有定义法、代入法、参数法、几何法、交轨法等，其中尤其关注轨迹纯粹性．

（四）运算方法

在明确运算方向的背景下，任何数学运算最终必须落实到具体方法与操作流程．解题教学中不仅要向学生阐述构思历程，而且要展示详细运算过程，这既是数学运算核心素养的基本要求，也是培养运算能力的具体操作，更是优化思维品质，提升核心素养的途径．

（五）运算程序

实施数学运算是理解运算对象、掌握运算法则、探究运算方向、选择运算方法之后面临的关键问题．设计有效、恰当、简捷的运算程序是破解具体问题的必由之路，更是解决同类及相似问题的普遍方法，达到举一反三、触类旁通的效果，是实施高效解题教学的重要策略．

（六）运算结果

数学运算最终目的是求解结果，不仅运算结果正确，而且追求最佳、最简结论，同时要善于反思、勇于质疑．反思是解题教学的核心．反思解题思路，培养思维发散性；反思解题过程，培养思维严谨性；反思解题结果，培养思维批判性；反思解题规律，培养思维创造性．

四、一题多解

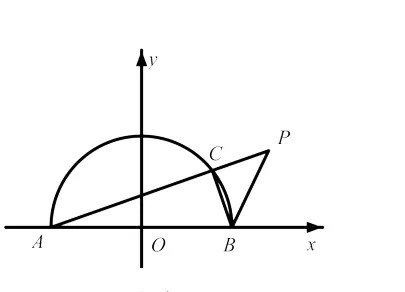
图2

解法1：本文约定半圆O与y轴正半轴交于点M；设 P(x,y)（x＞-1，y≥0 ） ； C(x0,y0)（x0＞-1）；设 ∠CAB=α由图 2得到 ∠PBX=∠PAB+

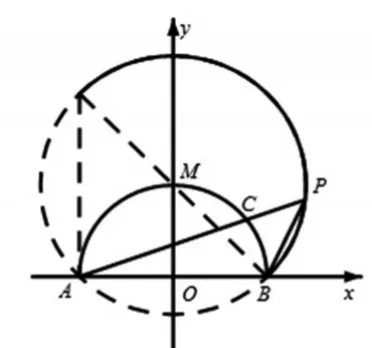
图3

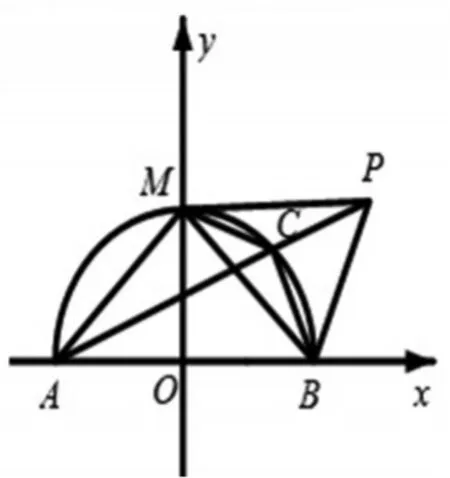
图4

解法2：如图4所示，连接PM，由同弧圆周角可得由圆内接四边形对角互补可得∠MAB+∠BCM=π；又 ∠MCA+∠PCM=π，于是可得 ∠BCM=∠PCM，依据三角形全等判定定理得到△PCM≅△BCM，则故动点P的轨迹是以M(0,1)为圆心，半径为的半圆，下同解法1．

当我们将图1中的曲线与有些线段隐藏就可以得到图5，便会发现问题的本质，即动点P对两个定点A(-1,0)、B(1,0)的张角为定值，依据平面几何相关知识，可知动点P的轨迹就是以AB为弦的某圆的一段弧．据此得到以下具有本源性的解法.

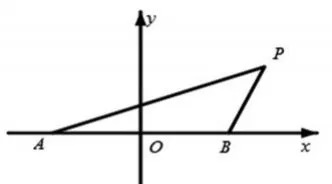
图5

解法3：由向量可得

依据向量数量积及算二次原理可得

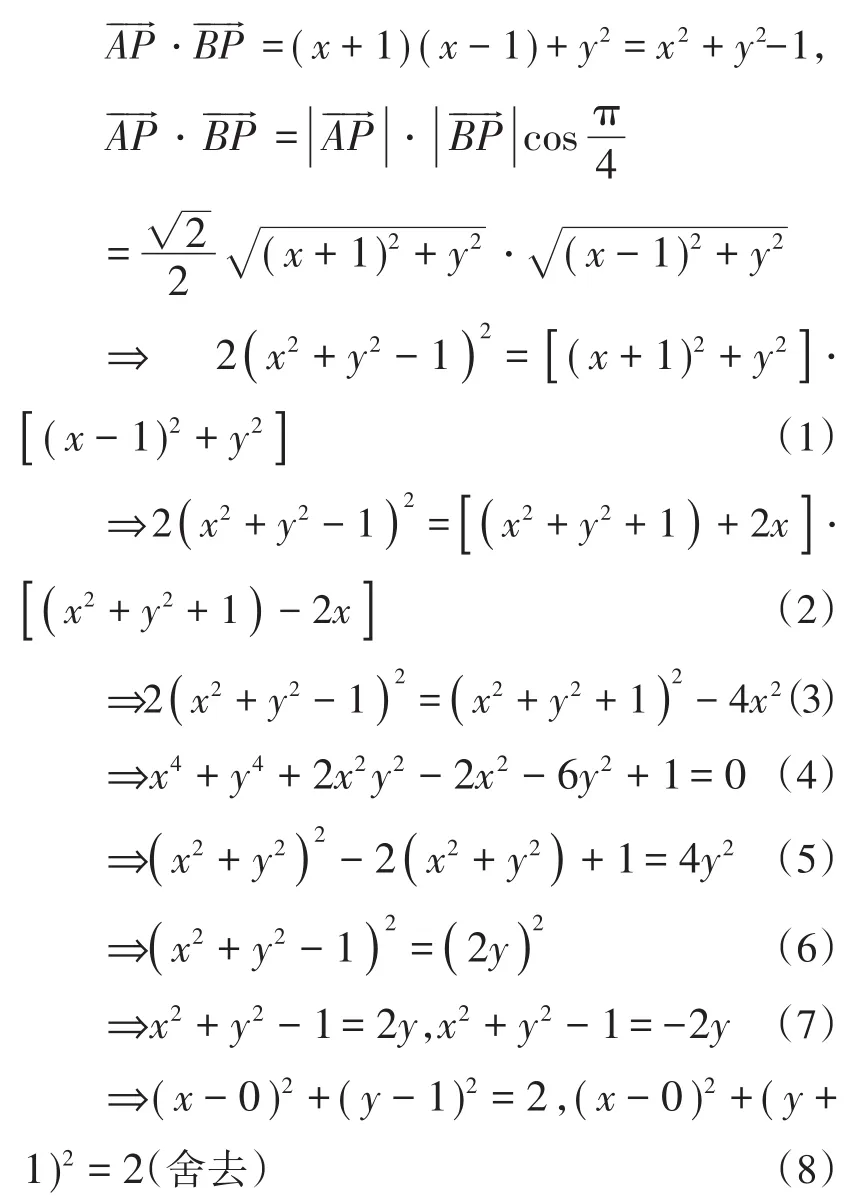
解法4：解法3步骤较多，我们可以适当简化．将（3）中的x2+y2及x2+y2-1看作一个整体，展开后就可以得到上述（5）及（7），下同解法3．

解法5：由图4可知依据同弧上的圆心角为圆周角的两倍，则动点P的轨迹在以AB为弦且点M(0,1)为圆心、半径为的圆弧上，下同解法1．

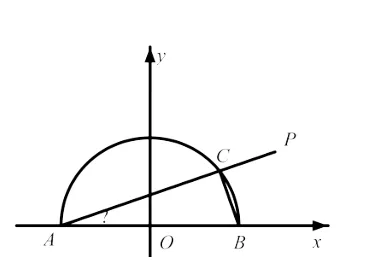
图6

解法6：由图6可得AP=AC+CP，又 CP=CB，则AP=AC+CB，利用Rt△ACB中的边角关系 可 知 AP=ABcosα+ABsinα=2cosα +2sinα.再由图6可得cos2α （11）

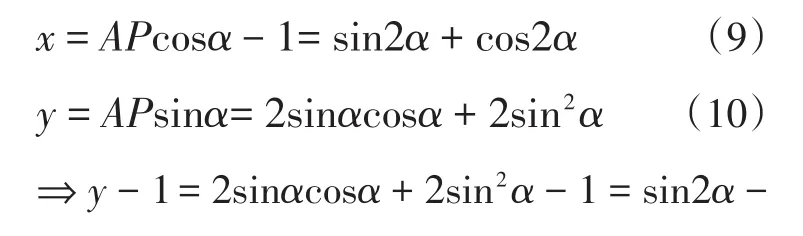
由（9）与（11）平方相加（消参数α）可得所求轨迹方程．

解法7：由题意可得三角形PCB是以PB为斜边的等腰直角三角形，如图2所示，我们可以将CP看作CB绕着点C逆时针旋转得到，依据复数知识可得

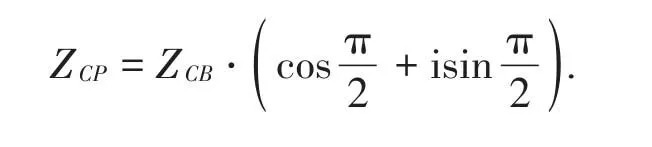
将相应的点的坐标代入上式并化简即可得到所求轨迹方程．

解法8：如图6，设直线AC的方程为y=k(x+1)（显然斜率存在），且与圆O的方程联立，再依据韦达定理中的两根之积得到

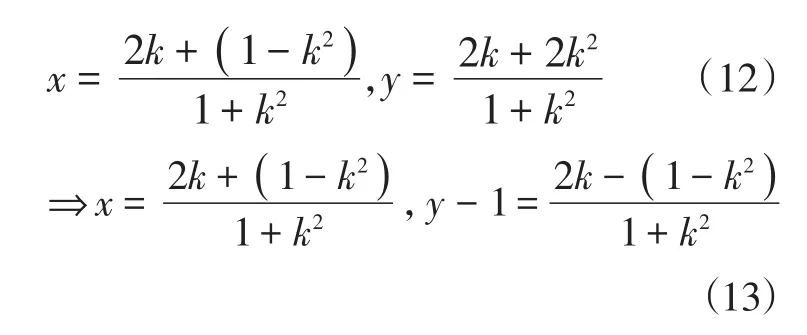
上述两式平方相加（消参数k）即可得动点P的轨迹方程．

解法9：显然过点P作射线PN，使得则如图7所示，过A作x轴的垂线与PN相交于点N.显然，四点A，B，P，N在以BN为直径的圆上，即圆心为直径BN的中点.又因为圆心必在弦AB的中垂线上，即点M为圆心，因此动点P的轨迹在以M(0,1)为圆心、半径为的半圆．

解法10：过C作x轴垂线交x轴于点D，过P作CD的垂线交DC延长线于点E.如图8所示，不难证明Rt△PEC≅Rt△CDB，得到PE=CD，则x=OD+PE，即

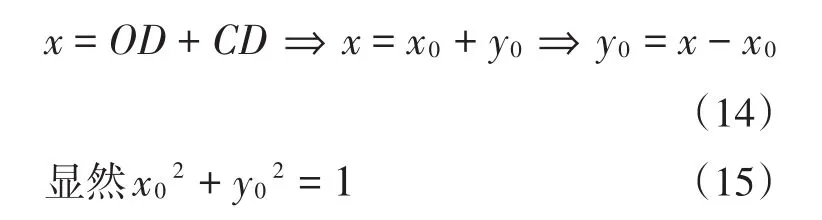
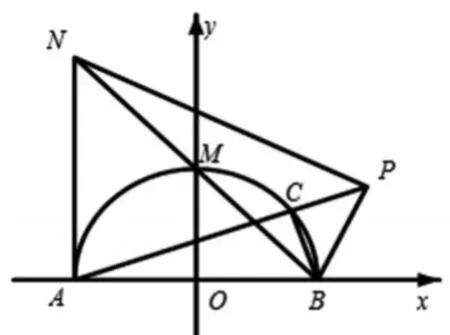
图7

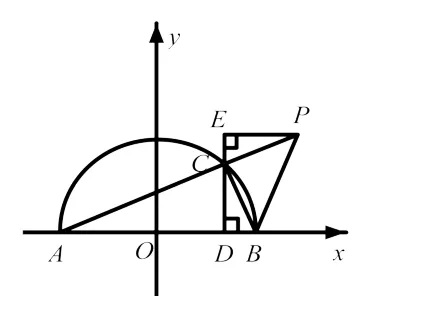
由于三角形PCB是以PB为斜边的等腰直角三角形，即

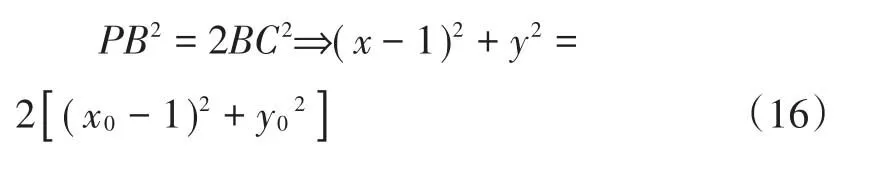
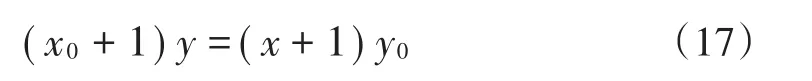
注意到三点A，C，P共线，则有将（14）分别代入（15）（17）得到

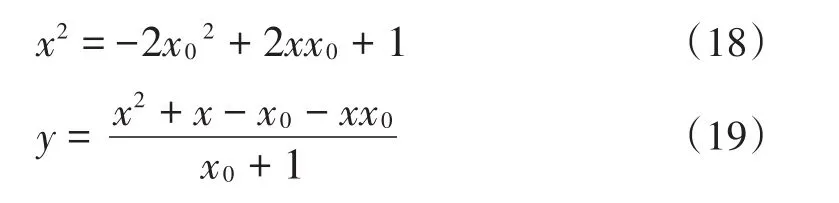
再将（18）代入（19）得到我们将（15）代入（16）得到

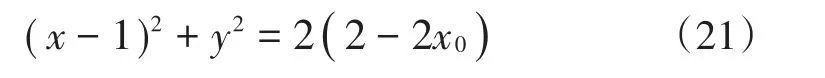
再将（20）代入（21）可得所求轨迹方程．

五、感悟反思

（一）命题陷阱

从上述剖析过程可知，动点P的轨迹方程为(x-0)2+(y-1)2=2（x＞-1，y≥ 0），因此其轨迹为半圆，轨迹长度为圆周长的一半，这正是选项A.不少学生没有注意到轨迹的纯粹性，误以为轨迹就是整个圆，这正是命题专家故意设置干扰项C的缘由．部分学生注意到y≥0，误以为轨迹就是圆(x-0)2+(y-1)2=2在x轴上方的部分，从而得到轨迹长度为该圆周长的四分之三，这是命题专家设置干扰项B的依据．正如上述解法3，不少学生误以为轨迹是两个圆，这是设置干扰项D的理由.针对选择题，我们必须研究命题专家设置干扰项的“理由”，这是精准解答选择题的关键，也是预防错误并得到正确结果的必经之路.

（二）反思质疑

波利亚将解题过程分为弄清问题、拟定计划、实施计划、回顾反思等四个阶段．弄清问题即剖析条件之间的关联，理解运算对象，掌握运算法则；拟定计划就是在探究运算方向的前提下，设计运算程序；实施计划就是选择运算方法并求得运算结果；回顾反思是最重要也是最容易忽略的一个环节，通过回顾所完成的解答，并重新考虑和重新检查这个结果和得出这一结果的思路，巩固知识，提高解题能力，优化思维品质，提升运算素养．

比如，对于解法2，轨迹为何是半圆呢？源于点C本身只能在半圆O上运动.对于解法3中的①→⑥，为何这样配方呢？有何依据？因为解法2从本源上确定其轨迹是圆的一部分，既然是圆就一定可以这样配方.解法3中怎么会出现两个圆呢？事实上，已知三角形一边与其对角，其动点轨迹本来就是两段圆弧，只是因为动点C在半圆O上运动，因此其轨迹只能是一个圆的一段弧.为何解法4中可以将x2+y2看作一个整体呢？其实，这并非是简单的换元法，而是因为解法2已经明确轨迹为圆的一部分.既然是圆，依据圆的一般方程特点：x2与y2的系数相同且不为零，这才是看作一个整体的缘由；客观地讲，由（9）与（10）消去参数α以及由（12）消去参数k并不容易，正是解法2作为铺垫，使得我们明确了运算方向，于是在（10）式与（12）式两边同时减去1，为后续消去参数奠定基础．这也再一次说明探究运算方向、选择运算方法（两式平方相加）并非空穴来风，而是建立在缜密分析的基础上.事实上，在解法6中，利用三角函数的值域，容易得到x＞-1，y≥0，正好与题意吻合，也恰好体现轨迹的纯粹性.上述解法6与解法8毕竟仅仅含有一个参数，相对不算太难，而解法10中含有两个参数x0，y0，必须承认，从（14）（15）（16）及（17）中同时消去参数x0，y0是十分困难的，笔者也是经历长时间摸索.遗憾的是，不少教师在实施运算时，往往重视运算方向、方法而忽视具体操作过程，不愿意甚至根本不舍得花时间来详细演绎运算过程，导致学生一看会做、一算就错、会而不对、对而不全．当涉及运算对象（x，y，x0，y0）较多，主要矛盾就是减元，这就是为何连续将（14）分别代入（15）（17），将（15）代入（16），将（18）代入（19），将（20）代入（21）的缘故，其终极目标依然是奔着解法2的结果（圆）而去．如果没有这一目标，几乎很难有效消去两个参数．

（三）不可分割

由上述分析过程，我们深刻感悟到数学核心素养之间你中有我，我中有你．它们既有区别又有联系，既各有侧重又和谐统一．数学运算往往与直观想象密切相关，上述解法3、解法4、解法6、解法8以及解法10（数学运算）都是建立在解法2以及解法7（几何直观）的基础上，通过几何直观，启迪解题思路；数学运算又与数据分析密不可分，数据就是信息，透过数据，发现本质，正是上述解法5中的数据，让我们联想到同弧上的圆心角为圆周角两倍，进而紧扣目标（圆）；同时数学运算还与逻辑推理不可分割，通过逻辑推理，发现隐含规律，上述解法3、解法4、解法6、解法8，尤其解法10中的逻辑推理过程非常复杂，在推理的同时关注运算，在运算的过程中体会推理，使得数学运算、逻辑推理、数据分析以及几何直观等核心素养融为一体，相得益彰，在解题活动中，感悟数学思想方法，积累数学思维的经验，在潜移默化中形成和发展数学运算素养．