高考题怎么改编（五）——平面向量篇

苏 玖

真题展现

（2018全国卷Ⅰ第6题）在△ABC中，AD为BC边上的中线，E为AD的中点，则=（ ）

图1

思维延伸

本题主要是两次使用三角形中线对应的向量，其实就是两个向量的加法运算的几何意义．如果点E不是中点，而是三等分点、四等分点等等，可以改编为：

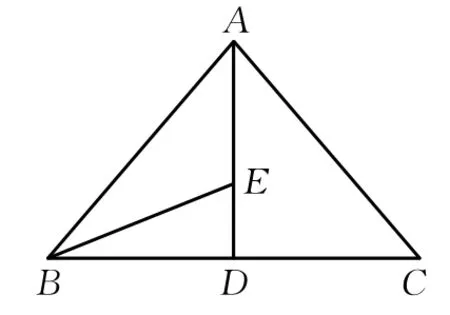
图2

拓展：在△ABC中，E为BC边上中线AD上的点，求x+y的值．

如果把“BE”改为“过E点任作直线”，就改编为：

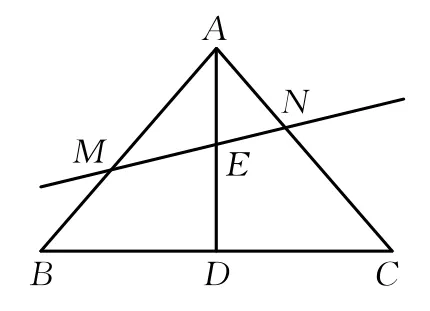
图3

如果改变图形的形状，由“三角形”改编为“平行四边形”“梯形”等等，如：

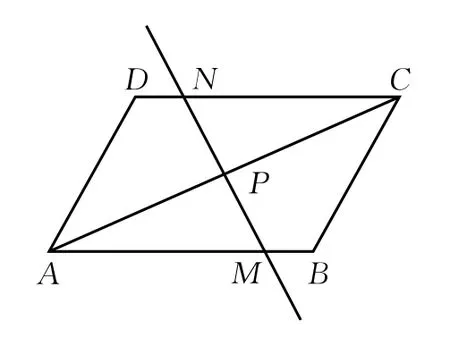
图4

当然也可以在三角形的一条边上插多个等分点，研究一系列的向量之和与数量积，于是有：

图5

如果三角形与圆整合，又可以有：

如果点O不是三角形外接圆的圆心，而是三角形内任意一点，于是又可以为：

点拨解析

原题解析：抓住D为BC边上的中点，E为中线AD的中点，于是有故选A．

改编1解析：因为所以，

拓展解析：因为所 以，所以所以x+y=．

改编2解析：由改编1拓展知，所 以，+．

改编3解析：因为+，

改编4解析：（1）证明：因为点P1，P2，P3，…，Pn是边AB上的n个等分点，所以，

改编5解析：【解法一】取AB中点D，所以，所以．又因为2x+y=1，所以O，D，C三点共线．

图6

因为点O为△ABC的外心，所以OD⊥AB，所以CD⊥AB．

【解法二】cos∠DAO=2=，

又因为2x+y=1，所以y=1-2x，②

改编6解析：因为·所以取BC中点D，

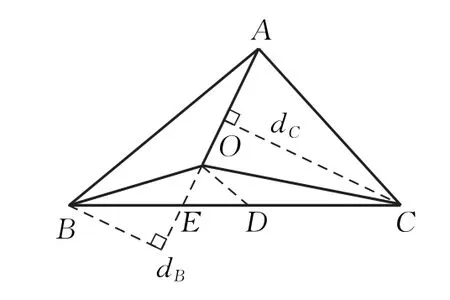
图7

回顾悟道

从上述各题的改编过程中可以看出，抓住平面向量的线性运算的几何意义，进行改编高考题或教材上的题目，是命题者常用的方法．改编途径：一是改编一个点的位置比例；二是定点改为动点，常数改为字母参数；三是改变平面图形的形状和特征，如三角形改为平行四边形、矩形、梯形、菱形等；四是三角形与外接圆或内切圆组合等等．

小试牛刀

题目：已知A，B，C为圆O上的三点，若则的夹角为____________．

提示1：将三角形特殊化，改为正三角形，则有：

（改编1）____________________________

提示2：将三角形改为等腰梯形，则有：

（改编2）____________________________

答案与解析

（改编1）△ABC是边长为2的等边三角形，已知向量a，b满足，