基于“三个理解”的平面向量单元教学构想①
陈志江
(常熟外国语学校 215500)
1 问题的提出
近年来,平面向量内容在模考、高考中逐渐加大了考查难度和力度,与此相对的是学生对向量问题的解决似乎越来越不理想.笔者在与师生的交流中了解到:学生们认为向量题解法灵活多样、变化多端、难以捉摸,有的题目甚至无从下手;教师们则认为该讲的都讲了,很多题目并不难,但学生错误率却很高,认为还是学生的数学素养差,同时也感到平面向量的教学越来越困难了.教与学出现了矛盾,《平面向量》这一单元到底如何教?让笔者陷入了深深的思考,笔者认为可能是教师在平面向量内容的教学中仅仅完成了书本知识的传授,站位较低,缺少高位的教学目标指引和一些整体构想,于是造成了学生对向量知识的理解不深刻,应用不灵活.
章建跃博士在其论文《中学数学课改的十个论题》中提出:“理解数学、理解学生、理解教学是进行新课程有效教学的三大基石.”这句话发人深省.关于“平面向量”这一单元的教学我们是否做到了“理解数学、理解学生、理解教学”?在反思后笔者写就本文,以苏教版教材为例(其他版本教材可参考),阐述在“三个理解”指导下对《平面向量》这一单元内容的教学设计构想,希望以此改进教学,在此抛砖引玉,请方家指正.
2 基于“三个理解”的《平面向量》单元教学构想
2.1 理解数学,将向量内容有机融入数学知识体系
理解数学是指教师不仅清楚数学知识本身是什么,能解各种数学题,也指教师清楚数学知识的产生背景、形成过程、形成方法,清楚数学知识的本质、结构及其与相关知识的联系.教师只有理解了所教学的内容,才会在教学设计中准确地确定教学的重点和难点,才不会“捡了芝麻丢了西瓜”.
在平面向量教学中,教师要清楚向量知识“来自何处,又去向何方”,还要清楚平面向量的知识系统(如图1),在此基础上我们才能把现成的、成熟的数学知识还原为生成的、发展的知识.传统观念下的中小学数学内容就是数、式、方程、函数及几何图形,而平面向量内容的加入如打开了一扇窗,透过这扇窗,可使学生领略到不少优美的数学景象.比如向量扩充了运算的对象和内涵,有向量的加法、减法运算(a±b=c)、向量的数乘运算(λa=b)、数量积运算(a·b=c),向量运算时运算对象从一元扩展到多元,这对于学生在今后的学习中进一步理解其他数学运算(如导数、矩阵、变换等),发展学生的运算能力具有奠基作用.在数学发展史上,向量的引入与寻求几何研究的新工具有很大关系,它是沟通代数、几何与三角函数的一种工具.在教学中要善于用向量语言和方法与这些内容有机整合,使学生认识到向量在平面几何、立体几何、解析几何和三角函数等方面的广泛应用,认识向量在更新完善数学知识结构方面的重要作用.
2.2 理解学生,既要对接还需发展学生的知识水平
理解学生是指教师清楚学生学习数学的基础、潜能、需求与差异,清楚学生学习特定数学知识已有的知识萌芽、生长点与潜在的困难,清楚学生的认知特点与认知规律.数学教学服务的对象是学生,教学设计是为学生更好地学习来设计教学.因此在教学过程设计前对学生的分析,教学问题的诊断显得尤其重要,只有较为深刻地理解了学生,教师在教学设计中才能准确地确定难点和关键点,反之,离开了对学生现状的准确把握,再漂亮完善的教学设计也达不到理想效果,正如苏霍姆林斯基说“没有也不可能有抽象的学生”.
向量的内容对学生来说是新知,我们要寻找好知识的最近发展区,主要是两个知识生长点:一是物理中矢量的相关知识;二是数学中实数的运算体系.教材充分考虑到这两点,在新知内容的展开时紧密结合学生的已有知识,根据学生的生活经验,创设丰富的情境,从大量的实际背景中抽象出向量的概念(数学模型);然后用数学的方法研究向量及其运算的性质;最后再运用数学模型去解决实际问题,这样一种“循序渐进,螺旋上升”的设计使对新知内容的教学变得容易且自然清楚,因此,就向量新知内容的教学而言并不困难.但如果教学停留于此,那么就把数学学习过程变成了识记的过程,而不是思考怎样用数学知识去解决数学问题的过程,学生的能力就得不到提高.事实上,向量教学的难点主要在于向量的应用,这也是学生的困难所在,如果学完了内容却不知道这有什么用及如何用来处理问题,那这样的教学一定是意义不足的、价值残缺的、也是没有深度的,所以我们应深入思考向量应用的教学,培育发展学生的应用能力.
2.3 理解教学,培育学生处理向量问题的四种意识
理解教学是指教师清楚教学的本质与功能,掌握一定的教学方法和教学艺术,清楚学生的认知规律和教学的基本原则,能够把教与学作为有机的、统一的、相互促进的整体来加以处理.基于笔者对平面向量单元内容教学的经验,将本单元的教学设计为四个层次,并深化教学目标为培育学生处理向量问题的四种意识,具体如下:
第一层次,在类比与比较中建构线性运算,培育学生基底化意识.
教材中向量内容是在与物理中一些矢量(如位移、速度、加速度、力等)的类比和数学中实数的运算和运算律的比较中逐步展开的.在引出向量概念时提出问题“位移和距离这两个量有什么不同”,又再现了数量的概念,并将其与向量作比较;在研究向量的加法时首先研究“两次位移后游艇的合位移是什么”,研究向量加法的运算律时直言为“交换律、结合律”引发与实数运算律的比较;在研究向量的数乘运算时以“质点做匀速直线运动下的位移问题”为引入,给出数乘的运算律后提出了思考“向量的数乘和实数乘法有哪些相同点和不同点”等等,教学中我们要充分认识到这些,设计好从数和矢量到向量的类比比较学习.
此时要达到建构好向量的线性运算体系尚且不够,还需要以“平面向量基本定理”来统领,该定理的本质就是:平面上任何一个向量总是可以由两个不共线的向量线性表出,这样才能“升华”学生对向量线性运算的理解.就定理本身而言,其内容与证明并不难,难就难在对定理的应用上,学生往往不清楚有了这个定理能解决什么问题,这说明学生对定理的理解并不深刻,即缺乏对向量问题通过基底化后来解决的意识.因此教学中我们要选择好典型问题,通过典型问题的解决培育好学生的基底化意识.
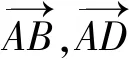
解法如下:

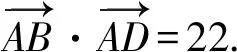
第二层次,从向量分解到向量的坐标运算,培育学生坐标化意识.
平面向量基本定理实际上是在对向量进行分解,当把一组基底取成互相垂直的单位向量时,就可在平面直角坐标系中定义平面向量的坐标表示了,因此,“平面向量基本定理”起到了承上启下的作用.向量的坐标化使形到数的转化变为可能,打开了向量与解析几何联系的窗户,为很多问题的解决开辟了新的道路.当然随之而来的是要探讨平面向量的坐标运算,加法、减法、数乘运算的坐标表示(进一步完善了向量线性运算的体系),以及后续学习的向量数量积运算的坐标表示.
同样,对向量的坐标运算我们也不能只停留在知道运算法则和会作运算上,更应培育学生应用向量的坐标化进行问题解决的意识.
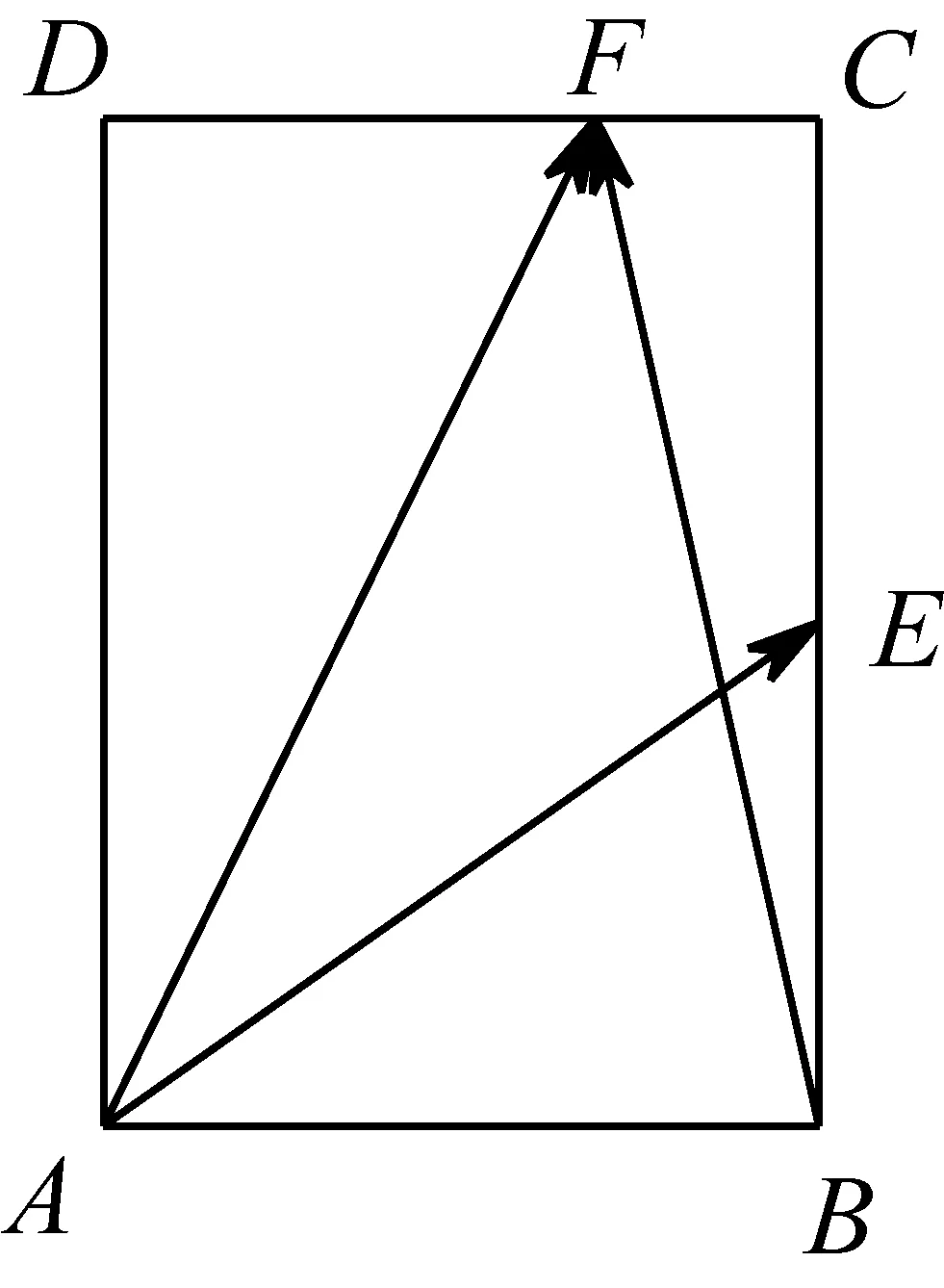
图3
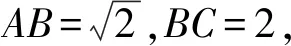
分析本题载体为矩形,存在两线垂直的条件,又加上AB,BC的长度已知,会给我们联想,建立坐标系,将向量进行坐标化.


从上例可以看出,坐标化解决一些几何问题可谓“四两拨千斤”.此类问题的几何载体,一般涉及正方形、矩形、等边三角形、等腰三角形、等腰梯形、直角梯形等,有时也会给已知一个定角和一些线段长度的不规则图形,均可尝试坐标化处理.这也为以后解析几何中进一步学习解析法埋下了伏笔.
第三层次,对数量积的物理性作数学抽象,培育学生数量化意识.
向量的数量积对学生来说是一种新的运算,在学习了向量的加法、减法、数乘三种运算后,教材从问题:“向量与向量能否‘相乘’呢?”引入可谓直击“要害”,简明自然,很好地引起认知冲突;然后从物理中的力对物体做功问题进行数学抽象,定义两个向量的数量积运算,直观形象,水到渠成,教学中要充分结合实际问题帮助学生理解运算含义.对数量积的运算律更是要注意与实数中乘法运算律及向量的数乘运算律进行比较,且要正确区分它们的相同与不同之处.向量数量积的坐标运算则是对向量坐标化的进一步完善.
在这一层次的教学中,重点是数量积的运算,难点则是数量积的应用,而学生大多对数量积运算的理解是很不深刻的,事实上该运算是向量与向量相乘和数量与数量相乘相互转化的桥梁(a·b=|a||b|cosθ,特别地a2=|a|2).数量积在向量条件的转化中有着广泛的应用,学生是否具有将向量进行数量化的意识直接关系着问题的能否解决.
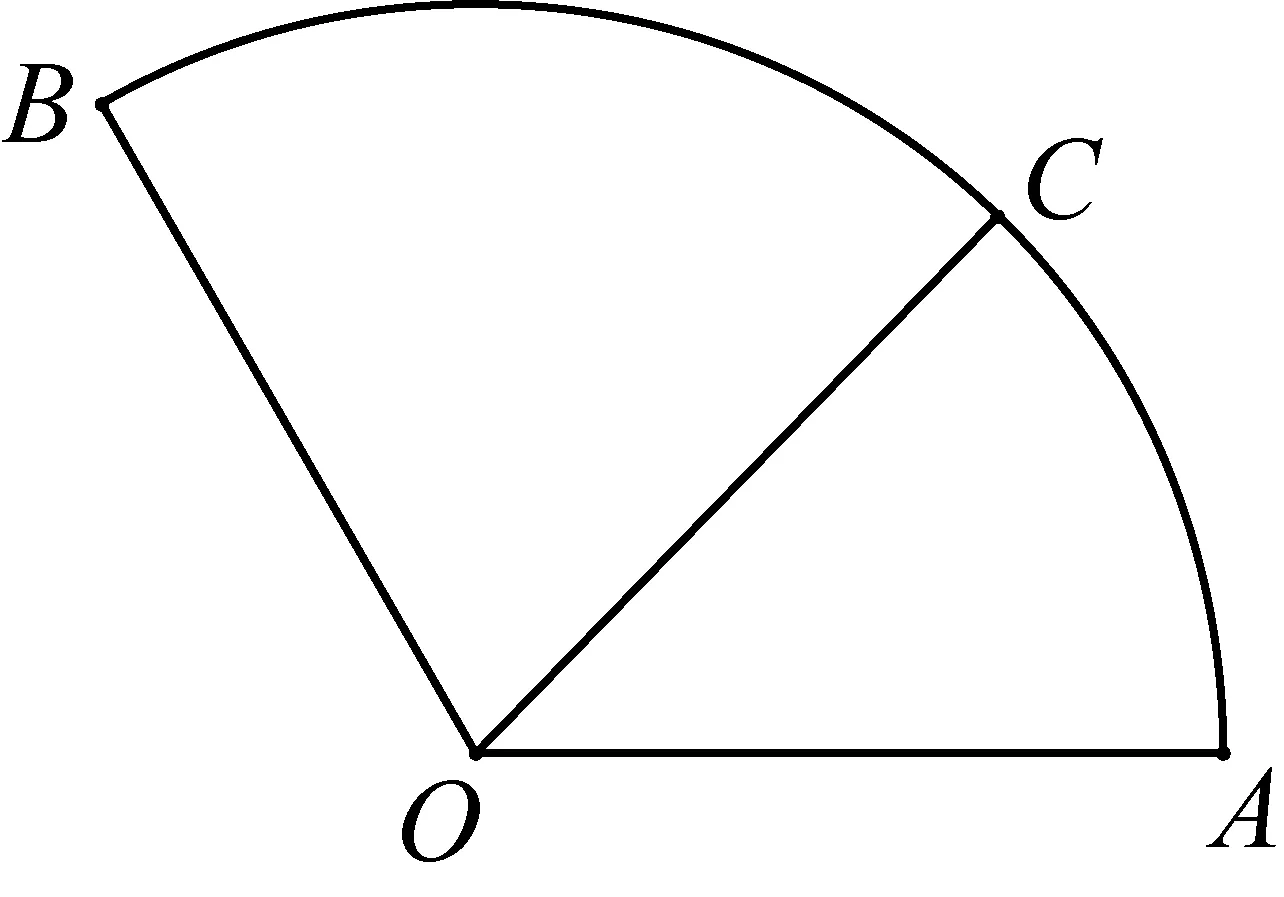
图4



则有1=x2+y2+2xycos120°,
即1=x2+y2-xy.

从而x+y≤2,当且仅当x=y=1时取等号.
故x+y的最大值为2.
解法二设∠AOC=α,则

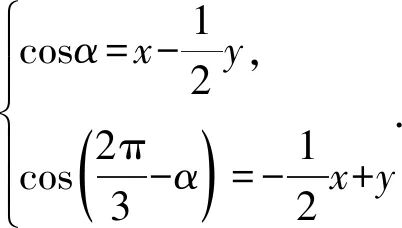


再如《解三角形》一章中,对“正、余弦定理”的证明就是对向量式子应用上述方法实施数量化,这当然是对学生数量化意识培育的又一个好机会.
第四层次,用向量实现代数与几何的转化,培育学生几何化意识.
这一层次是本章最后一节内容“向量的应用”,篇幅虽不长,但内蕴很丰富,需要深入挖掘.在学习向量基本知识后,我们应有意识地将向量与三角恒等变形,与几何、代数之间的相应内容进行有机的联系,并通过比较和感受向量在处理三角、几何、代数等各不同数学分支问题中的独到之处和桥梁作用,认识数学的整体性.这样有助于学生认识数学内容之间的内在联系,体验数学的发现与创造过程.
在这个层次中,培育学生的几何化意识尤为重要,其实,向量内容中很多式子都有其几何意义.比如向量的加法和减法对应着平行四边形或三角形,向量的模对应着线段的长度,两非零向量的数量积为0对应着相互垂直,两向量的数量积也可视作一个向量的模与另一个向量在其方向上投影的乘积……但学生在问题解决中往往缺少这种意识,不能把数与形有机结合.如下题目,此题在我市实测难度为0.18,就暴露出了学生的上述问题.
题目(2011年苏锡常镇二模第12题)平面内两个非零向量α,β满足 |β|=1,且α与β-α的夹角为135°,则|α| 的取值范围是.
分析本题解决需要学生有几何化的意识,由三角形法则构造出一个三角形,这样条件中的向量模长与边长对应,向量夹角与三角形内角角度对应,问题就可完成转化.当然如果能联系圆的相关知识的话,那么就更简单了,于是有以下两种解法.
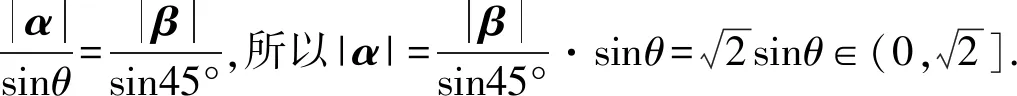
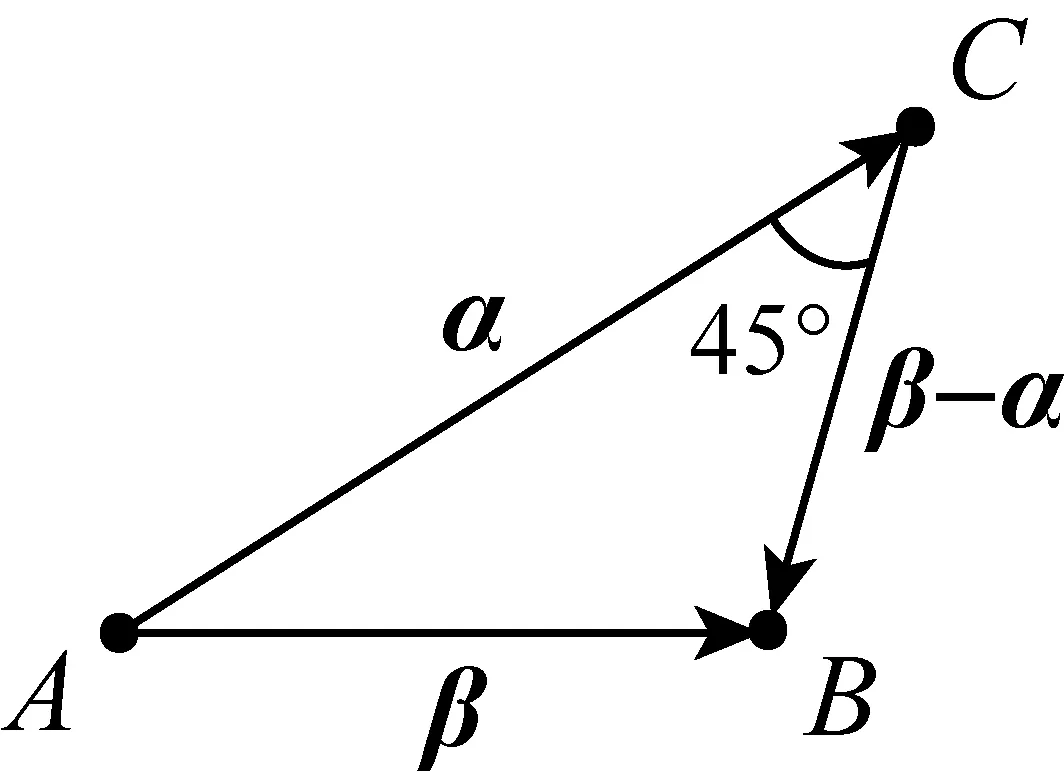
图5
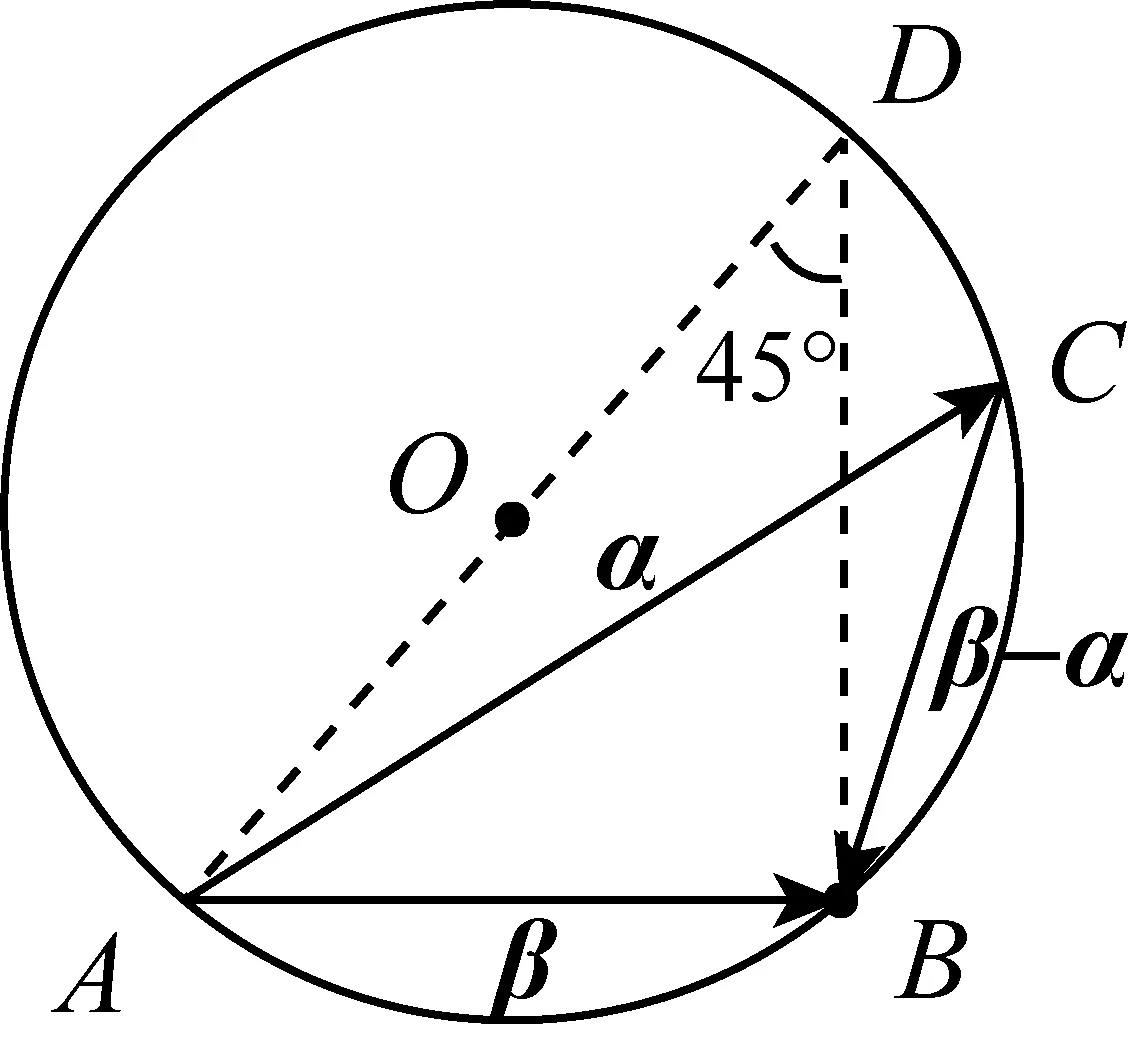
图6
3 结语:宏观的课程与微观的课堂之间应有中观的单元教学设计
什么是教学?这一问题可谓仁者见仁,智者见智.希伯特将其描述为“在课堂中围绕内容,并促进学习目标达成的师生、生生活动”.教学的任务是创造一个学生参与的环境来引起学生思考,并且让学生解释他们知道什么以及是如何思考的,所以它受到教师、学生和学科知识之间关系的制约,这需要我们教师考虑到各方面的因素并做出的决策和行动,也就是要充分思考“三个理解”.笔者认为,在宏观的课程与微观的课堂之间还应有中观的单元教学设计,在培养学生核心素养为目标的教学中,单元教学设计尤为重要,它应是教师教学活动的重心所在,也是教学研究的永恒主题.“三个理解”指导下的单元教学可以有多个角度的思考与实践,它是一个需要经历种种迷茫、困惑、冲突、感悟、发现,否定——肯定——再否定——再肯定的过程,它不可能一蹴而就,也不可能一劳永逸,但据此会产生新的变革、扩大、深化、再创造,一线教师正应在这样的过程中修炼自己的教学行为,提升教育智慧.

