正多面体的历史及其现代教育价值

张晓雪 代 钦

(内蒙古师范大学数学科学学院 010022) (内蒙古师范大学科学技术史研究院 010022)

1 前言

古希腊贤哲们观察和探索自然时发现了正多面体的存在并给出了正多面体只有五种的证明．柏拉图等哲学家将正多面体作为描述自然本原存在的基本几何形式．中世纪后，开普勒亦将正多面体和球体结合的几何模型作为行星运动的宇宙模型．用正多面体刻画自然和宇宙是否符合科学，我们在这里不作讨论．重要的是，人们已普遍认可正多面体的存在是神圣的．对哲学家、数学家、天文学家、艺术家和科学家来讲，它们的存在具有无限的魅力．我们在想象正多面体的时候，脑海里便浮现出毕达哥拉斯、柏拉图、欧几里得、笛卡儿、开普勒、伽罗瓦、埃舍尔、帕乔利、达芬奇、达利等一长串伟大人物的名字．

自古以来，正多面体在学校数学教育中亦具有不可低估的价值．正多面体作为特殊的多面体是几何学从二维空间过渡到三维空间的重要内容，对于刚刚接触空间几何体的学生来讲，自然是一个适宜的桥梁．它们不仅帮助学生更容易地从平面过渡到三维空间，还能够激发学生学习数学的兴趣和探索数学奥秘的热情．这些都可以从它们的历史发展脉络以及各国教科书中的呈现得以表征．

2 正多面体历史概述

人类最初通过矿物结晶的形状了解到了正四面体、正六面体、正八面体和近似的正十二面体，而人工制作的正十二面体，是在二千几百年前埃特利亚(意大利中部的古国)遗物中以青铜器的形状出现．近几十年人们发现很多散射虫的结构呈现出正多面体的形状．而且有一种病毒的结构呈现出了正二十面体的形状，晶体硼(B12)的结构单元也正是正二十面体，如图1．

图1

对于三维空间内只有五种正多面体的历史可以追溯到古希腊时期．据说此时埃及人已经知道了正四面体、正六面体和正八面体．毕达哥拉斯定理、无理数的发现者、万物皆数思想的倡导者古希腊哲学家、数学家、天文学家毕达哥拉斯(Pythagoras,BC580-500)及其学派已研究得出正多面体只有五种的结论，如图2，即由全等的正三角形生成的正四面体、正八面体和正二十面体以及由全等的正方形生成的正六面体、由全等的正五边形生成的正十二面体．而由其它全等的正多边形是不能生成正多面体的．并且他们认为五种正多面体除正十二面体以外的四种分别构成宇宙的四要素，即火、土、气和水．而正十二面体可以认为是牵强的与宇宙相关联在一起．

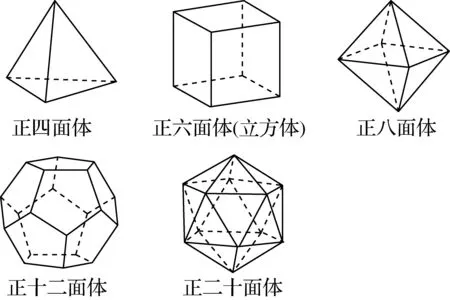
图2

进一步发展这种正多面体宇宙观的是古希腊哲学家和教育家柏拉图(Plato，公元前427-347)．柏拉图在其《蒂迈欧篇》中详细讨论了在理智的宇宙结构中正多面体扮演的角色[注]柏拉图.柏拉图全集第三卷[M].王晓朝，译.北京:人民出版社，2003：265.．他设想宇宙起始只有两种三角形，一种是底角为45°角的等腰直角三角形，一种是底角分别为30°和60°角的直角三角形，由这两种三角形就可构成四种正多面体，它们分别对应构成宇宙五种微粒中的四种．火微粒是正四面体，气微粒是正八面体，水微粒是正二十面体，土微粒是正六面体，而正十二面体则构成第五种元素，柏拉图称其为精英[注][英]斯蒂芬·F·梅森.自然科学史[M].上海：上海译文出版社，1980:27.．正多面体也因此被称为柏拉图多面体或柏拉图立体．

而与柏拉图同时期的古希腊数学家泰阿泰德(Theatetus，具体生卒年不详)被一般认为是第一个证明了只存在五种正多面体的人．其证明的依据是构成一个立体角的所有角之和要小于360°．

继泰阿泰德之后的集古希腊古典数学之大成者——欧几里得(Euclid,公元前330-260)，他著成了世界数学史上第一个数学公理体系著作《几何原本》，其第13卷18个命题以严谨的演绎推理，详细论述了正多面体相关问题．

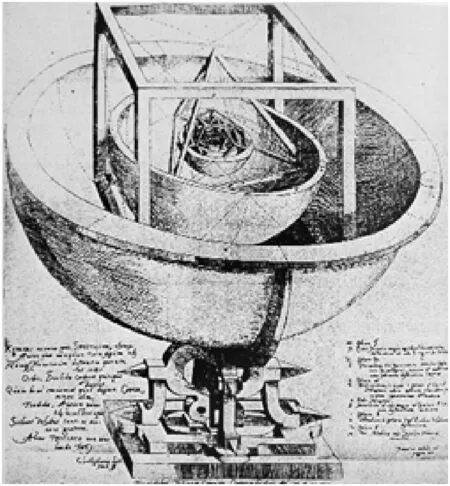
图3

16世纪被誉为“天空立法者”的约翰·开普勒(Johann Kepler，1571-1630)将正多面体的研究从古希腊时期带入了近代．开普勒从欧几里得《几何原本》中了解到，每一个正多面体都可以完美地内接在一个球体中．于是在他《宇宙的奥秘》一书中记载着他对柏拉图多面体与六大行星运行轨道间和谐关系的惊喜发现．如图3，即若土星运行轨道在正六面体的外接球上，那么木星的运行轨道就在正六面体的内切球上．然后在正六面体内切球内，内接一个正四面体，那么正四面体的内切球就是火星的运行轨道．依此方法就得到从外到内的这样一个顺序：土星→正六面体→木星→正四面体→火星→正十二面体→地球→正二十面体→金星→正八面体→水星，最中心是太阳．

而此时法国哲学家、数学家勒内·笛卡儿(René Descartes，1596-1650)正在探寻能将正多面体统一描述的永恒真理．他通过研究五种正多面体顶点的数量、面的数量和边的数量间的关系，最终得出了v-e+f=2，其中v为顶点数，e为边数，f为面数，笛卡儿终于解开了它们的神秘面纱，而且这个公式可以适用于所有多面体．遗憾的是，最后出于对宗教的忌惮，笛卡儿并没有将这个重要发现公诸于世[注]AMIR D.ACZEL.DESCARTES’ SECRET NOTEBOOK[M].NEW YORK:Broadway Books,2005:227.．我们今天知道这个公式被称为欧拉公式．在笛卡儿之后，德国数学家、物理学家欧拉(Euler,1707-1783)也独自发现了一般多面体意义下的这个公式，流传至今．

19世纪后半期开始了在四维以上空间内研究正多面体，在期刊“American Journal of Mathematics”创刊号(1879年)上刊登着一篇重要文章，它介绍了四维空间中正多面体有六种，星形正多面体有十种等重要发现．

正多面体不仅在几何学中有重要地位，在代数学中也扮演着重要角色．如代数中的重要内容——群，其中五次对称群分解的一个特殊群Ⅰ与正二十面体有着相对应的旋转对称性，而这个特殊群“Ⅰ”正是取自正二十面体英文单词“icosahedron”的首字母．[注][日]大栗博司.用数学的语言看世界[M].尤斌斌，译.北京：人民邮电出版社，2017：227.

3 数学教科书中的正多面体

正多面体历史悠久，这也使它承载着丰富的教育内容，蕴含着深刻的教育价值．而教科书是直接反映正多面体重要教育价值的载体．教科书是人类一代一代传承知识与智慧的基本工具．在历史上的几何学教科书中正多面体也占据着一席之地．

3.1 历史上数学教科书中正多面体简述

欧几里得《几何原本》这部伟大著作也是毫无变动地被使用了两千多年的教科书．正如前文所言，其第13卷中的18个命题全部围绕正多面体相关问题叙述．其中命题13-17分别论述了五种正多面体的作图问题，主要通过在球内建立正多面体，而该卷最后一个命题也是整部《几何原本》465个命题中的最后一个命题，命题18证明了只存在五种正多面体．显然这是一个完美的收尾．

在18、19世纪西方教育改革中大大简化了《几何原本》内容，之后如雨后春笋般地出现了新的几何学教科书．即使是在新几何教科书中，正多面体亦有不同程度的体现．

1888年美国GEORGE WENTWORTH和DAVID EUGENE SMITH所著的教科书《PLANE AND SOLID GEOMETRY》在先介绍了多面体概念后给出正多面体定义，即一个多面体的面是连续的正多边形，且它的多面角相等，这样的多面体叫做正多面体．接着进一步介绍只有五种正多面体的证明，并探究如何用平面图形(展开图)制作正多面体．

1920年美国HERBERT E.HAWKES、WILLIAM A.LUBY和FRANK C.TOUTON所著的教科书《PLANE AND SOLID GEOMETRY》中给出的正多面体定义是：“一个凸多面体，如果它的面都是全等正多边形，且它的多面角都是全等的，那么它就是正多面体．”其后给出只有五种正多面体的解释．

1903年英国H.S.HALL和F.H.STEVENS所著的教科书《A SCHOOL GEOMETRY》中并没有明确给出正多面体的定义，而是在介绍欧拉公式之后，引出只有五种正多面体的证明，并结合展开图进行介绍．

吕乃刚先生译，张奠宙先生作序的1998年俄罗斯数学教科书《直观几何》有专门一节内容介绍正多面体．通过考察五种正多面体的形状特征给出正多面体概念性的描述，即每一个正多面体的所有面都是相同的正多边形，在每一个顶点集聚着同样数量的棱，而相邻的面在相等角下毗连．然后对五个正多面体的顶点、边和面间的数量关系进行讨论，探究出欧拉公式，而后探讨其展开图及制作过程．

2003年美国Michael Serra所著的教科书《Discovering Geometry》(《发现几何》)第十章第三节棱锥体和圆锥体的“探索”栏目在简单介绍正多面体历史的基础上提出如何制作五种正多面体的问题．

2009年中国香港TW Wong和WS Wong所著的数学教科书《New Century Mathematics》首先在初三之前立体图形的学习中，将正多面体及其制作过程作为特殊情况予以介绍，最后在初三阶段进行总结归纳，由五种正多面体探究出欧拉公式．并对正多面体的历史，包括柏拉图、欧拉公式等进行了简要介绍．

1985年台湾师范大学科学教育中心主编的教科书《高级中学基础数学统合上册》，在共四章中有一章专门讨论多面体问题，而该章三节内容分别是多面体、欧拉公式和正多面体．不仅明确给出了多面体及其面、棱、顶点、多面角和正多面体的概念，对只存在五种正多面体进行了证明，还对我们可以不加证明即可使用的欧拉公式进行了详细的证明．所以，无论是从正多面体所占教科书内容的比重来讲，还是从教科书对正多面体内容的呈现方式来看，都体现着台湾对正多面体内容的重视程度之大，也充分反映着正多面体所具有的教育价值．

不难想象，各国中小学数学教科书中与正多面体相关的内容不胜枚举，这里不再一一列举．

3.2 外国数学教科书中正多面体内容个案——日本教科书中的正多面体

由历史上数学教科书中的正多面体内容可知，正多面体内容越来越受到人们的重视，尤其是美国、日本等发达国家的中小学数学教科书中正多面体内容更加丰富．这里作为个案，重点介绍日本现行数学教科书中正多面体内容设置情况．

日本中小学数学教育十分重视正多面体相关内容的学习，大多以作图、剪纸和拼图、制作模型等实践活动来实现学习任务．日本现行启林馆数学教科书对正多面体内容在中小学都有呈现，知识讲解较为系统，涉及内容较为全面．

日本小学数学教科书并没有直接给出正多面体的概念，多数是基础的立体几何内容，如感知并认识正方体、长方体和球等立体图形，通过探究正方体、其他柱体和椎体展开图，以及探究“平行四边形可以做什么”等活动初步了解多面体图形，这里并没有上升到谈及多面体或正多面体的概念．事实上，正方体就是正六面体，因此小学正方体的学习也为以后正多面体的学习埋下伏笔．

在初中《数学1》“各种各样的立体”设置了柱体、锥体等多面体图形后引入多面体的概念，即用一些平面包围的立体叫做多面体，且根据其平面的数量，分为四面体、五面体、六面体……．在下面的“数学展望台”中介绍了正多面体，给出：“在多面体中，所有面都是正多边形，聚集在一个顶点的面的数量也相等且没有凹陷的叫做正多面体．”并指出早在2000年以前人们就已经知道了正多面体只有五种．

从这里也直接链接到“数学广场：考察一下正多面体吧”，首先给出了五种正多面体及其透视图与展开图，接下来是五个问题：“①把267页的展开图组装起来，制作正二十面体吧，如图4；②正四面体一个顶点有几个正三角形聚集在一起？正八面体、正二十面体呢？③在一个顶点周围，有六个正三角形聚集在一起的正多面体吗，为什么？④在求正十二面体边的数量和顶点的数量时，下面的先生和女士给出如下做法，如图5，请说明他们的想法．考察一下五种正多面体的面的形状，顶点、边和面的数量吧，完成如图6的表格；⑤通过上述表格，求以下五种正多面体‘顶点数-边数+面数’的值吧，你发现什么了？”对于⑤问旁边有个提示，“对于⑤所考虑的值所蕴含的规律，瑞士数学家欧拉已经发现，认识一下欧拉吧．”这样，便自然地与数学史知识相遇了.

高中在《数学A》“空间图形”当中再次给出了多面体的定义，即由几个多边形围成的空间图形叫做多面体．并具体指出，构成多面体的多边形叫做多面体的面，面的顶点、边也叫做多面体的顶点、边，不在同一面内的两个顶点所连线段叫做多面体的对角线，以及多面体由它的面数决定它的名称，如四面体、六面体等．下面首先给出了凸多面体的定义，即在多面体中，面上的两个顶点所连线段在多面体内部的叫做凸多面体．在凸多面体定义的基础上给出正多面体的定义，即在凸多面体中，各个面是完全相同的正多边形，各顶点所聚集的面数、边数都相等的叫做正多面体.

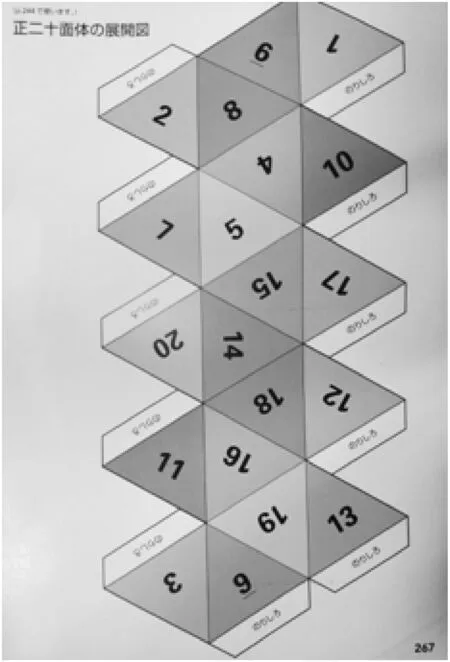
图4

图5

图6

接下来给出了欧拉的多面体定理，即v-e+f=2,v为顶点数，e为边数，f为面数．要求学生探究、感受并确定其定理的成立．在“Colum”栏目介绍了“正多面体的立体”．“Colum”栏目就是设置与本节内容相关联的话题．具体介绍内容如下：如图7，试着将正六面体通过各边中点进行切割，考虑留下的立体图形．它的顶点数为12，边数为24，面数为14，于是可以使得欧拉多面体定理成立．这个图形是由8个正三角形和6个正方形构成的，被称为立方八面体.

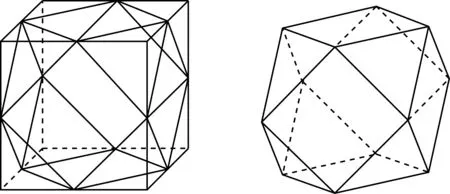
图7

在紧随其后的“研究”栏目中对只有五种正多面体进行了如下解释．

正多面体存在的两个必要条件：

①聚集在一个顶点的面数为3个以上；

②顶点处多边形的内角和要小于360°．

根据①、②具体到正多面体的面也就是正多边形，它的内角要小于120°，而构成正多面体的正多边形就只有正三角形、正四边形和正五边形三种．

(1)当正多面体的面为正三角形时,

正三角形的一个内角为60°，根据条件②一个顶点聚集的面数是3、4、5中的任意一个．1条边是两个面的交线．(其中v为顶点数，e为边数，f为面数．)

A.当一个顶点聚集的面数是3时，如图8，

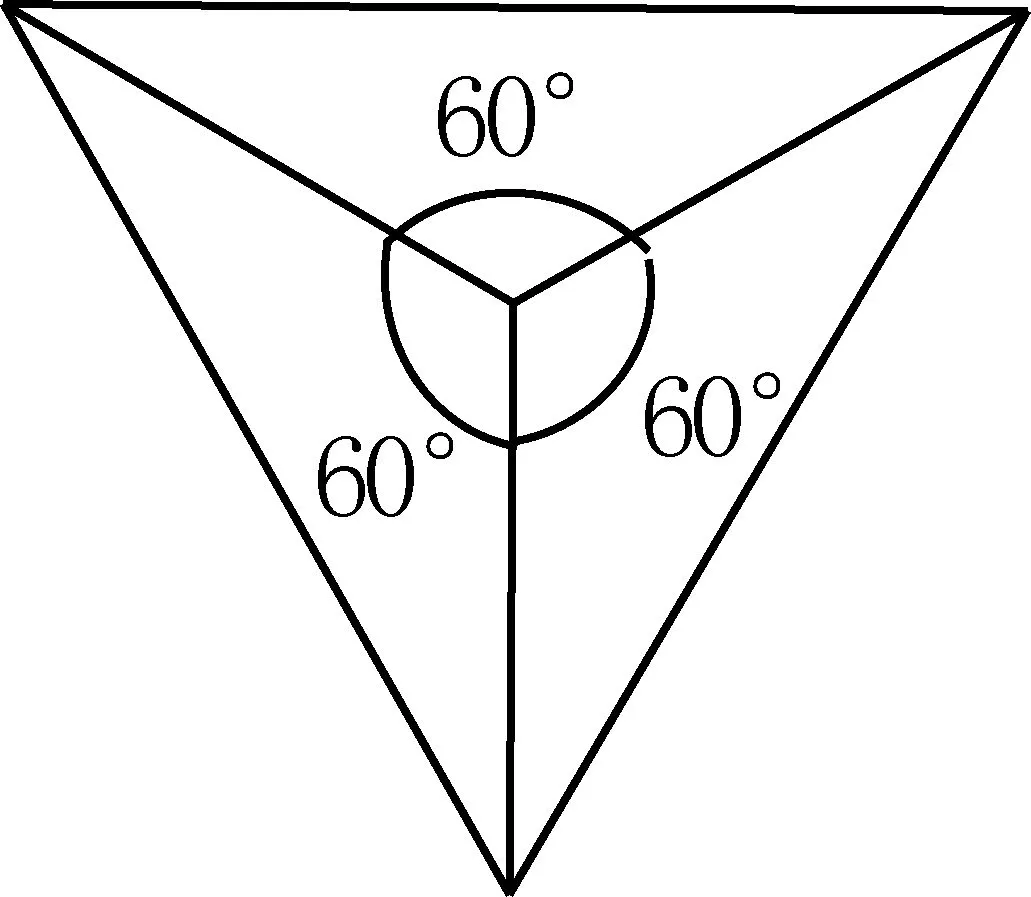
图8

因为v=3f÷3，e=3f÷2，

v-e+f=2

所以f=4.

即得正四面体.

B.当一个顶点聚集的面数是4时,如图9，

图9

因为v=3f÷4，e=3f÷2，

v-e+f=2

所以f=8.

即得正八面体.

C.当一个顶点聚集的面数是5时,如图10，

图10

因为v=3f÷5，e=3f÷2，

v-e+f=2

所以f=20.

即得正二十面体.

(2)当正多面体的面为正四边形时,

正四边形的一个内角为90°，根据条件②一个顶点聚集的面数只能是3．与(1)同理可得f=6，即得正六面体.

(3)当正多面体的面为正五边形时,

正五边形的一个内角为108°，根据条件②一个顶点聚集的面数只能是3．与(1)同理可得f=12，即得正十二面体.

在教科书末尾设置的“课题学习”中也安排了正八面体的动手制作课题六项：①将1边长为5cm的正八面体展开图组装起来，然后寻找相互平行的面吧；②把课题1制作好的正八面体一面放置水平台上，然后画出它的透视图；③若正八面体的边长为1，则求出课题2所画图形的面积．接下来是考察正八面体与正四面体的关系：④将1边长为5cm的正四面体展开图组装起来，尝试能否把它装进课题1制作的正八面体中，如图11．另外，将正四面体像课题2中正八面体那样放置，对它们的高度进行比较吧；⑤将1边长为10cm的正四面体展开图组装起来，尝试能否把课题1制作的正八面体装进正四面体中．另外，试着考虑正四面体体积是正八面体体积的几倍；⑥像课题1、课题4、课题5那样，也可以做其它各种各样的立体，调查它们的性质并进行比较．

图11

在《数学活用》当中设置一节为“正多面体的作法”，清晰、详细地呈现了通过折纸制作成的五种正多面体的作法，如图12，展示的是正四面体的制作过程，其它具体内容这里不再赘述．

图12

小学正多面体的学习主要是一种直观的、简单的对长方体、正方体的学习，目的是为培养学生空间感，从而建立空间想象，为以后正多面体的学习做好扎实的铺垫．初中在认识了很多立体图形的基础上介绍多面体，其定义“用一些平面包围的立体”直观易懂但不甚严谨，同样也给出了正多面体的定义，这些也是初中“立体几何”作为一种实验几何的体现．并通过融入数学史料阐明正多面体只有五种，然后在“数学广场”部分对五种正多面体及其透视图与展开图进行考察，通过五个问题培养学生动手操作能力、分析问题能力和逻辑推理能力，对于这些问题并没有给出答案，而是再次通过数学史料给学生以寻找答案的线索．

高中对多面体及其面、顶点、边和对角线都给出了明确定义，随后在给出凸多面体定义的基础上给出了正多面体的严格定义．接下来出现了欧拉的多面体定理，并在“Colum”栏目讲述了立方八面体，从这里也说明了正多面体满足欧拉多面体定理，但满足欧拉多面体定理的多面体不一定是正多面体．此外，这里也渗透了另一个数学史知识，即阿基米德多面体[注]阿基米德多面体：相对于每种柏拉图多面体的面都是同样的，古代科学巨匠阿基米德(Archimedes,BC287-212)发现的13种多面体的面是两类或多类不同的多边形，其环绕着多面体每一个顶点按照一定次序出现．实际上也可以将阿基米德多面体理解为是把柏拉图多面体的顶点截掉或对柏拉图多面体进行扩展或推扭得到的，即从柏拉图多面体演化而来．，立方八面体就是从柏拉图多面体演化而来的阿基米德多面体的一种．在“研究”栏目也给出了正多面体存在的两个必要条件及只有五种正多面体的证明，且从证明方法上来看，正是毕达哥拉斯思想和泰阿泰德证明方法有机结合的体现．高中正多面体的内容是对初中正多面体内容的深化和延伸，也可以看成是对初中“数学广场”内容的回应．而教科书末尾设置的“课题学习”中也安排了动手制作课题六项，《数学活用》中通过折纸完成正多面体的制作，这些开放性栏目都是为学生动手操作能力和创造性思维的培养而设置的．

从整体上看，日本小学、初中再到高中的正多面体内容抓住了学生的阶段性特点，合理安排知识的呈现方式，其实秉承的则是知识间有效衔接的理念．

4 正多面体的教育价值

事实上，上述日本教科书个案已经很好地展现了正多面体的教育价值．

正多面体的学习有助于学生对数学史的了解．在今天学习正多面体内容时仍然可以学习到很多历史知识．例如欧拉公式，伟大数学家笛卡儿和欧拉独立得出的永恒真理，让我们在了解数学史的同时也体验毕达哥拉斯、柏拉图、欧几里得、笛卡儿、欧拉等伟大数学家们孜孜不倦、追求探索的精神．柏拉图和开普勒的数学化的宇宙观也让我们感受到数学的奥秘．

正多面体的学习有助于学生认识到数学与其他学科间的关联性．数学作为自然科学的工具，描述自然科学的语言，定然不会独立存在．从正多面体的历史可以看到，它的发展伴随着天文学的发展、哲学的追问以及人类思想的进步．除此之外，正多面体也应用在很多美术、建筑、工艺等艺术作品中，如我们常见的骰子、魔方、黄金比例结构等．

正多面体的学习有助于发展学生对数学学习的系统性和完整性．正多面体虽然是空间立体图形，但它不一定就是要在高中才具体学习．日本中小学数学教科书中对正多面体知识的呈现就较好地体现了知识的螺旋上升和递进发展．这种有效衔接使得学生对知识的掌握更加系统和完整．

正多面体的学习有助于培养学生的数学核心素养．正多面体本就是特殊的多面体，而由正多面体探索出的一般规律“欧拉公式”，又是从特殊到一般的推理，这对学生逻辑推理能力的培养大有裨益．而在推理中较多的运算过程对数学运算能力也是一种培养．正多面体的展开图是三维到二维的转化，正多面体的制作以及作图又是二维到三维的发展，这些都有助于对学生直观想象能力的培养．

图13

正多面体的学习有助于对学生动手能力、开放性思维的培养．正多面体内容中有着丰富的动手实践价值．《几何原本》中全面严谨的正多面体作图方法、美国、香港教科书中正多面体的动手制作以及日本教科书中正多面体嵌套的复杂制作等，都已表明人们自古以来便注意到正多面体作图及制作对学生动手能力和开放性思维培养的重要性．而在制作正多面体时也涉及到重要的黄金分割比．如图13，y∶x=1.618……的矩形,3张上述的矩形即构成正二十面体．(注：本文通讯作者代钦教授在日本学习和工作期间，东海大学平野叶一教授团队开发中小学数学校本课程时，用黄金比例矩形制作正二十面体，并给代钦教授展示，提供了具体材料．)而且学生在动手的同时更能深刻感受到数学的对称美、和谐美以及“数学神奇”、“数学好玩”．

正多面体的学习有助于对学生数学学习兴趣的培养．无论是从数学史的角度还是动手操作“数学好玩”的角度，都能够激发学生对数学学习的兴趣，感受在本以为冷冰冰的公式背后有着太多有意思、有意义的故事．

5 结语

正多面体教育价值的重要性不言而喻，今天只是简要的一瞥，正像日本著名数学家一松信所说：“仅仅详细论述正多面体的历史，就能写成一本书”．[注][日]一松信.正多面体を解く[M].東京：東海大学出版会，1983：24.正多面体在以自然为源头的时间长河中，流淌在古希腊哲学、天文学、数学、建筑、艺术等学科之中，它更多的价值亟待我们探索和重视．要知道这些并不是我们创造的，有时发现比创造更为重要．可以看到，美国、英国、日本、俄罗斯、中国香港等地的数学教科书中的正多面体，都是以知识为主，采用不同设计形式，为学生能很好地掌握正多面体的知识、发展学生动手操作能力、培养学生创造性思维而呈现．遗憾的是，目前尚未在中国大陆现行数学教科书中发现正多面体的内容．而在过去中学数学教科书中有不少正多面体的内容，如1961年人民教育出版社出版的《高级中学课本立体几何》(暂用本)第二章第四节中有正多面体概念和对只存在五种正多面体的讨论．这也是一个值得商榷的问题．由于正多面体的相关内容丰富，在以后的研究中继续探讨．