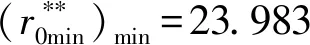做平面运动滚子从动件盘形凸轮机构的泛类尺寸综合问题

林梦杰 李延平 常 勇

集美大学机械与能源工程学院，厦门，361021

0 引言

针对做平面运动滚子从动件盘形凸轮机构，常勇等[1-8]归纳和概括得到广义Ⅰ类尺寸综合问题和广义Ⅱ类尺寸综合问题。广义Ⅰ类尺寸综合问题，即已知从动构件系统尺寸、输出件推程始终位置和位移规律、许用压力角、位于连杆平面Σ2的滚子中心位置等，求解凸轮轴心的解区域、最紧凑的机构尺寸解等。广义Ⅱ类尺寸综合问题，即已知从动构件系统尺寸、输出件推程始终位置和位移规律、许用压力角，位于机架平面Σ0的凸轮轴心位置等，求解滚子中心的解区域、最紧凑的机构尺寸解等。上述两类尺寸综合问题有明显的前提，前者是已知滚子中心，求解凸轮轴心；后者是已知凸轮轴心，求解滚子中心。

本文研究的问题是，已知从动件系统尺寸、输出件推程始终位置、位移规律和许用压力角等条件，求解滚子中心、凸轮轴心解区域、最紧凑的机构尺寸解等的尺寸综合问题，即泛类尺寸综合问题。

1 问题的准确描述

如图1所示，德国海德堡高速印刷机机构的泛类尺寸综合问题的描述如下：已知机架长度l0、摇杆长度l5、初位角θ50、行程角βm、推程运动角Ф0和运动规律、推程许用压力角[α]、凸轮转动方向滚子中心C，凸轮轴心O1分别位于连杆平面Σ2、机架平面Σ0上，求解滚子中心C、凸轮轴心O1的解区域、最紧凑机构尺寸解等。

图1 高速印刷机机构的构型Fig.1 Mechanism-form of high-velocity printing machine

2 理论基础和若干重要结论

2.1 固定坐标系Oxy和浮动坐标系O2uv

图1所示的演化构型中，凸轮轴心、滚子中心位于机架、连杆平面，反映泛类尺寸综合的特征。固定坐标系Oxy指固连于机架平面Σ0上，以O为原点、O→x为x轴正向、O→y为y轴正向的坐标系。浮动坐标系O2uv指固连于连杆平面Σ2上，以O2为原点、O2→u为u轴正向、O2→v为v轴正向的坐标系。

2.2 广义Ⅰ类尺寸综合问题解法[3]

据文献[3]，在连杆平面Σ2上任取一点作为滚子中心C(u,v)，根据类速度图原理和推程压力角α≤[α]，任一瞬时均存在瞬时区域套Γ(x,y)/瞬时边界∂Γ(x,y)。根据相应解析公式[3]，绘制整程∠P20Hx-θ1线图。

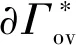
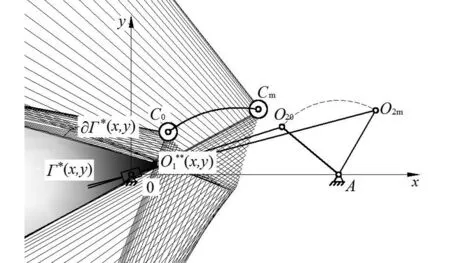
图2 Γ*(x,y)/∂Γ*(x,y)存在(开放性态)Fig.2 Γ*(x,y)/∂Γ*(x,y) exists(oponed)

2.3 最优凸轮轴心和凸轮最小基圆半径的求解

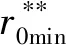
图3 Γ*(x,y)/∂Γ*(x,y)存在(封闭性态)Fig.3 Γ*(x,y)/∂Γ*(x,y) exists(sealed)

3 Γ*(x,y)/ ∂Γ*(x,y) 的性态多样性

在连杆平面Σ2上，探索、遍历性选取一系列点作为滚子中心C(u,v)，采用文献[3]方法及解析公式编制通用程序，生成对应的Γ*(x,y)/∂Γ*(x,y)。

滚子中心C(u,v)不同时，Γ*(x,y)/∂Γ*(x,y)存在性态多样性：

(2)Γ*(x,y)/∂Γ*(x,y)不存在时，如图4所示，Γ*(x,y)是空集，Γ*(x,y)/∂Γ*(x,y)不存在。

图4 Γ*(x,y)/∂Γ*(x,y)”不存在Fig.4 Γ*(x,y)/∂Γ*(x,y) not exists

文献[3]因在连杆平面Σ2上取点有限，仅仅发现了Γ*(x,y)/∂Γ*(x,y)存在的情形。新的研究发现：①Γ*(x,y)/∂Γ*(x,y)可能存在②Γ*(x,y)/∂Γ*(x,y)存在时，有开放性态、封闭性态。

4 C、O1解区域的遍历搜索求解方法

4.1 选定简约遍历区域Σ [2]和Σ[0]

连杆平面Σ2、机架平面Σ0无限延展，若据此搜索求解，计算工作量大、不经济、效率低，因此，应尽量压缩简约遍历区域Σ[2]和Σ[0]的选择范围。同时，应能保证反映、呈现重要的现象、规律和特征。

通过预估和评判，在连杆平面Σ2、机架平面Σ0上，选定图5所示的简约遍历区域Σ[2]：

(1)

和Σ[0]：

(2)

图5 Σ[2]和Σ[0]及其离散——网格化Fig.5 Σ[0] and Σ[0] and its discrete grid

Σ[2]、Σ[0]的选定需要兼顾求解的可靠性和经济性。可靠性指问题目标解必居其中；经济性指求解工作量显著减小。

4.2 Σ[2]和Σ[0]的离散——网格化

如图5a所示，对Σ[2]和Σ[0]分别沿u、v和x、y方向离散——网格化：

Δ=up+1-up=vq+1-vq=xj+1-xj=

yk+1-yk=10-m(mm)

(3)

其中，m为离散指数，取自然数，根据求解精度要求而定。

对于任一网格节点C(up,vq)和O1(xj,yk)，有

(4)

p=pmin，pmin+1，…，pmax

pmin=int(-0.7l0/Δ)pmax=int(0.7l0/Δ)

q=qmin，qmin+1，…，qmax

qmin=int(-0.4l0/Δ)qmax=int(l0/Δ)

和

(5)

j=jmin，jmin+1，…，jmax

jmin=int(-0.4l0/Δ)jmax=int(l0/Δ)

k=kmin，kmin+1，…，kmax

kmin=int(-0.7l0/Δ)kmax=int(0.7l0/Δ)

4.3 滚子中心C的解区域和非解区域

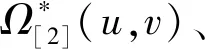
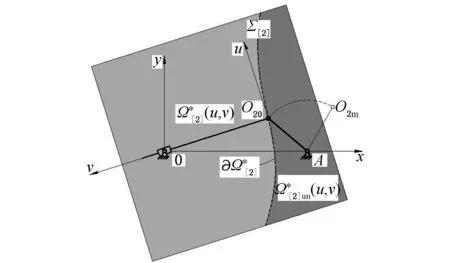
图6 滚子中心C的解区域和非解区域 Fig.6 Union solution domain and non-union solution domain of roller center C

4.4 滚子中心C的并解区域和并非解区域

(6)

图7 滚子中心C的并解区域和并非解区域 Fig.7 The roller center C’s union solution region and not union solution region

4.5 凸轮轴心O1的并解区域和并非解区域

5 最紧凑机构尺寸解的存在性与求解方法

如图9所示，根据2～4节，得最紧凑尺寸解的具体求解思路和步骤：

图8 凸轮轴心O1的并解区域和并非解区域 Fig.8 Union solution domain and non-union solution domain of cam axis O1

图9 空间曲面S* *、谷脊线J* *和谷底点P* *Fig.9 Space surface S* *,ridge line J* * and bottom point P* *

6 机构综合示例

求解步骤如下：

(2)如图9所示，据已知条件、步骤(1)和第5节步骤(1)～步骤(4)，解得空间曲面S* *。