两端式自动化立体仓库布局堆垛机调度

蔡安江 薛晓飞 郭师虹 蔡 曜 郭宗祥 赵项利

1.西安建筑科技大学机电工程学院，西安，710055 2.西安建筑科技大学土木工程学院，西安，710055 3.河北省带式输送机工程技术研究中心，衡水，053020

0 引言

自动化立体仓库作为生产物流以及CIMS加工模式的中枢环节，集存储、转存、运输、分发功能为一体，代表了当今生产物流的发展趋势[1]。在高密集储存需求下，两端式自动化立体仓库得到了更为广泛的应用。为更加有效地进行管理，提高整体作业效率，两端式自动化立体仓库要求对货位和堆垛机的运行路线进行优化，以缩短存储时间，提高效益[2-3]。

国内外学者对自动化立体仓库的优化调度问题进行了大量的研究。HACHEMI等[4]采用整数线性规划研究了自动化立体仓库的进出库调度问题；庞龙等[5]将蚁群算法与遗传算法相结合来解决了拣选作业模型优化问题；REGATTIERI等[6]对堆垛机的停靠点策略进行了研究，构建了策略评估模型，以此来提高仓库作业效率；朱文真等[7]通过禁忌搜索算法改进遗传算法的变异算子，利用遗传禁忌混合算法解决了复合命令序列下的堆垛机路径优化问题。以上研究主要针对堆垛机的某一种作业方式，未综合考虑堆垛机单一命令作业和复合命令作业。MA等[8]提出一种基于集成学习策略的多目标优化算法，解决了立体化仓库调度问题；王进业等[9]针对旁通式立体仓库的工作效率问题，建立了同时考虑堆垛机出口选择和拣选路径的组合优化模型，采用结合了自适应邻域法的遗传算法进行求解。以上研究虽然综合考虑了堆垛机的两种作业方式，但未考虑复合命令作业方式中的出/入库任务交替进行所引起的起始点变化问题。杨文强等[10]建立了兼顾质量和路径的多目标优化模型，并采用改进的多目标禁忌搜索算法以实现调度优化求解；柳赛男等[11]为提高立体仓库出/入库操作的效率，研究了基于库区分配策略和货位分配策略的优化问题，并采用基于Pareto最优解的遗传算法对问题进行了求解。上述研究中，货物的出/入库台均在调度优化之前已经确定，而对于两端式自动化立体仓库，合理的出/入库台的选择也会缩短堆垛机的行走路程和作业时间，从而提高堆垛机工作效率。

基于此，本文针对两端式自动化立体仓库布局堆垛机调度路径模型进行研究，综合考虑堆垛机单一命令作业和复合命令作业两种方式，将货物的出/入库台分配纳入调度模型，运用涡流搜索(vortex search ，VS)算法进行优化求解，来提高算法求解效率和自动化立体仓库的存储效率。

1 调度优化问题与假设

1.1 问题描述

两端式仓库布局作为一种常见的自动化立体仓库模式，在实际生产生活中得到了广泛的应用，其出/入库台分别位于货架的两端，外部输送系统需连接出/入库台，故平行于货架区设置。图1为两端式仓库布局结构图，在自动化仓库每个巷道上设置1台堆垛机，巷道两端各设置1个库台，2个库台均可用于货物的入库和出库。入库货物由外部起始点运输至左右两端的出/入库台所用的时间相同；出库货物从左端出/入库台或右端出/入库台出库，再运输至指定输送点的时间也相同。

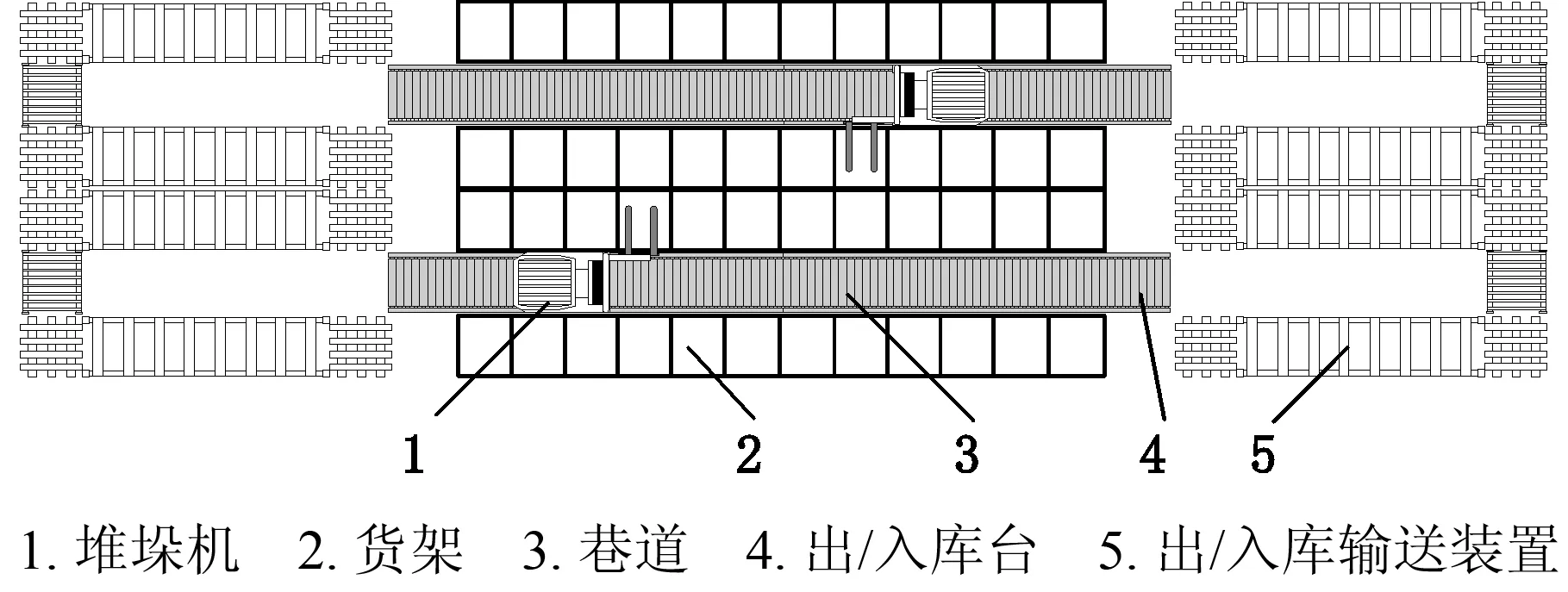
图1 两端式仓库布局结构图Fig.1 Layout structure of warehouse with double ended

堆垛机在存取货作业中存在两种作业方式：单一命令(SC)作业方式和复合命令(DC)作业方式[12]。堆垛机进入仓库仅进行1次存货或取货的操作为SC作业方式，堆垛机进入仓库进行1次存货和1次取货的操作为DC作业方式。该布局的自动化立体仓库的系统如图2所示，为单控制器双队列排队形式，出/入库任务指令被发送至堆垛机控制系统后，先经系统调度优化算法处理成合理的任务序列，然后再控制堆垛机进行操作。由此可见，因DC作业方式将出库作业和入库作业合为堆垛机一次复合作业，所以减少了堆垛机从出/入库台到货位之间的往返次数，大大提高了作业效率。然而在一批出/入库作业任务中，出库任务与入库任务的数量一般不相等，所以堆垛机不可避免要进行SC作业。

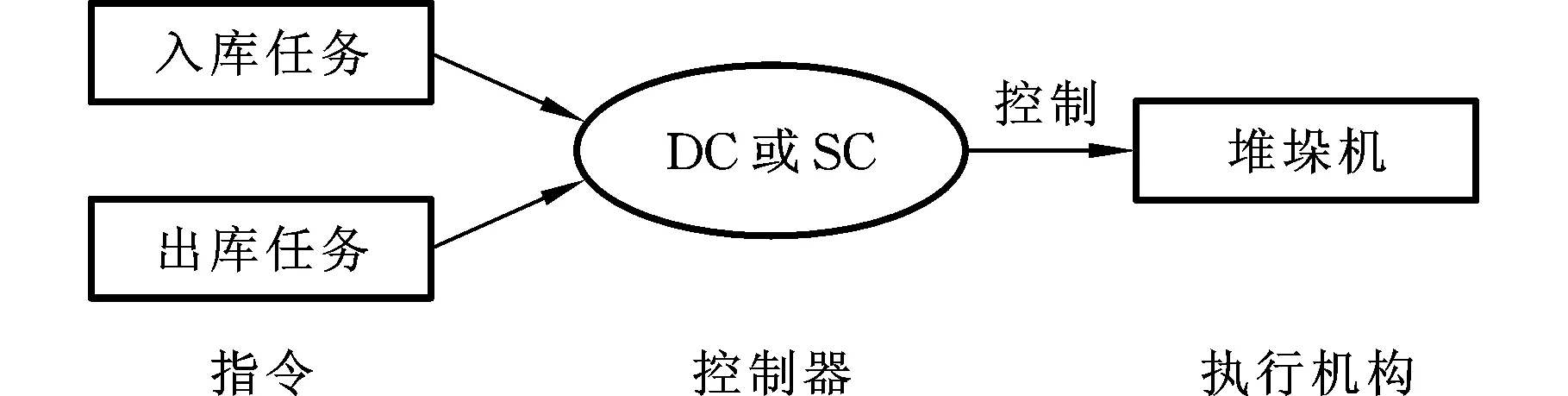
图2 单控制器双队列排队形式Fig.2 Single controller queue with two queues

对于一个出/入库作业订单，只需要确定每个出/入库货位的库位坐标(即待入库货物的入库货位坐标和待出库货物的出库货位坐标)即可，而对每个货物的出/入库台不作规定，将其作为堆垛机路径调度优化的一部分。由分析可知，执行第一个出/入库作业时，若该任务为入库作业，则该入库货物的入库库台为堆垛机执行完上一个出/入库作业订单后所停留的库台，若该任务为出库作业，则堆垛机执行该出库作业的起始位置为堆垛机执行完上一个出/入库作业订单后所停留的库台；堆垛机执行到最后一次任务时，若该任务为入库作业，则堆垛机返回至最近的库台，若该任务为出库作业，则该出库货物的出库库台为离堆垛机最近的库台。

由上述分析可知，要提高自动化立体仓库的作业效率，使其更好地适应生产物流的需求，就需要考虑堆垛机不同的出/入库序列运行的调度问题，如何将1个出/入库作业订单中的作业任务进行排列，组成DC作业和SC作业，使堆垛机运行时间最短。因此，本文针对两端式自动化立体仓库布局模式，提出了适用于该情况的DC/SC作业方式，并在此基础上建立堆垛机调度模型，进而进行优化研究。

1.2 基本假设

为方便研究问题，在两端式自动化立体仓库布局中，对固定货架和堆垛机的运行参数作如下设定：

(1)固定货架有I列、J层，共IJ个货位，各货位的长度为l，高度为h。设第i列、第j层货位的坐标为(i，j)，左端出/入库台IOj的坐标为(0, 1)，右端出/入库台IOk的坐标为(I+1, 1)，左右两端库台均可用于货物的入库作业和出库作业。

(2)堆垛机货叉运行速度恒定，对任一货位的拣选时间固定，不随该货位在拣选路径中的拣选顺序不同而发生变化。设堆垛机水平方向运行速度为vx，垂直方向运行速度为vy， 2个方向的运动是独立的，运行速度恒定，忽略堆垛机启动时间和制动时间。

(3)堆垛机在作业过程中，1次最多只能装载1件货物，固定货架的每个货位尺寸相同且货架中每个货位也只能存放1件货物。

通过以上基本假设可知堆垛机自货架位置(xa,ya)运行至货架位置(xb,yb)所需要的时间：

2 两端式仓库形式堆垛机调度模型

综上分析可知，本文所建立的堆垛机调度模型应解决两个问题：出/入库任务排序；出/入库货物库台选择。故在建模过程中，入库货物的入库库台和出库货物的出库库台在两端各有2个出/入库台可供选择，而实际情况是每个货物对应的出/入库台是由堆垛机执行该任务所用时间最短来决定的。

两端式堆垛机完成所有SC作业任务和DC作业任务需要的时间为

(1)

式中，T为完成该出/入库作业订单所需的总时间；TSCi为第i个SC作业任务所用的时间；TDCj为第j个DC作业任务所用的时间；m为SC作业任务的数量；n为DC作业任务的数量。

对于SC作业方式，假设堆垛机装货和卸货所用的时间相等，则

TSCi=TIOjPi+TPiIOk+2τIO

(2)

j,k∈1,2

其中，TIOjPi表示执行第i个SC作业任务时，堆垛机由装载货物的出/入库台运动至Pi货位的时间；TPiIOk表示执行第i个SC作业任务时，堆垛机由Pi货位运动至装载货物的出/入库台的时间；τIO表示堆垛机进行一次装/卸货物操作所用的时间。

由此，当有m个SC作业任务时，堆垛机运动总时间为

(3)

对于DC作业方式，同样假设堆垛机装货和卸货所用的时间相等，则

TDCj=TIOjP2j-1+TP2j-1P2j+TP2jIOk+4τIO

(4)

其中，TIOjP2j-1表示执行第j个DC作业任务时，堆垛机由装载货物的出/入库台运动至P2j-1货位的时间；TP2j-1P2j表示堆垛机从入库货位到出库货位的时间；TP2jIOk表示在当前任务序列中，第j个DC作业任务的出库货物到下一个入库作业的出/入库台，堆垛机的运行时间。

由此，当有n个DC作业任务时，堆垛机运动总时间为

(5)

综上所述，堆垛机完成一出/入库作业订单，所需要的总时间为

(6)

在一批出/入库作业任务中，出库作业任务与入库作业任务的数量一般不相等，因此我们假设在一批出/入库作业任务中，有n1个入库作业和n2个出库作业，取Q1=max(n1,n2)，Q2=min(n1,n2)。故此得出，该批出/入库作业订单由Q2个DC作业任务和Q1-Q2个SC作业任务组成。基于此，堆垛机完成该批出/入库作业订单的运行总时间为

(7)

则完成这批出/入库作业订单时，堆垛机最优路径模型为

g(T)=minT

(8)

3 出/入库调度路径优化

在求解自动化立体仓库堆垛机出/入库调度问题时，通常采用的遗传算法、粒子群算法等智能算法需要多次迭代才能找到近似最优解，且容易陷入局部最小，收敛效率低。针对这些不足，本文在建立的堆垛机调度模型的基础上，采用涡流搜索算法[13]进行调度路径优化。涡流搜索算法是在随机搜索和模式搜索基础上提出的一种启发式优化算法，它采用了一种根据迭代次数自适应调整搜索半径的策略，参数较少，迭代迅速，能够在较短的时间内找到最优解[14]。该算法可以提供搜索行为的探索和开发之间良好的平衡，通过使用自适应步长调整方案的搜索行为模拟涡流现象，具有操作简单和搜索能力强的突出优点[15]。涡流算法的搜索能力超过了单解的模拟退火算法、模式搜索算法和群解的人工蜂群算法，操作简单且搜索能力强，不需要设置过多参数，只需考虑迭代次数/候选解集大小以及搜索空间上下界等参数[16]。

3.1 涡流搜索算法的思想

在初始阶段，涡流搜索算法提供高效的探索行为，而当算法收敛到局部解附近时，则开始进一步的局部开发，使当前解向着最优解逐步逼近[15]。在迭代过程中，用最好的候选解S′∈Ct(s)替换当前解，并将其作为下一次迭代过程中半径的内环中心，产生新的候选解集Ct+1s；若最优解S′∈Ct+1s优于全局最优解，则更新全局最优解记录，并将最优解作为下一次迭代过程中缩减半径后的内环中心，重复上述过程直至满足结束条件，输出全局最优解记录，如图3所示。

图3 涡流搜索算法的搜索过程Fig.3 Search process of vortex search algorithm

3.2 编码设计

任务编码是进行算法优化求解的第一步，为了方便问题的处理，采用基于任务编号序列排序的整数编码方法将堆垛机接到的入库任务进行编号，组成一段编码，将堆垛机接到的出库任务在入库任务编号的基础上进行编号，组成另一段编码，同时将每个出/入库任务的入库库台和出库库台写成两段编码，用1、2表示出/入库任务的库台选择。

3.3 涡流搜索算法的步骤

针对两端式自动化立体仓库堆垛机调度模型，采用涡流算法进行调度优化，具体步骤如下。

(1)确定涡流搜索空间的初始中心。在D维空间中，第j维的取值范围为Ej=elj,euj，j=1,2,…,D，则涡流搜索空间的初始中心为

μ0=(μ01,μ02,…,μ0D)

μ0j=(elj+euj)/2

其中，el、eu均为D维向量，表示搜索空间的上边界和下边界，el=(el1,el2, …,elD)，eu=(eu1,eu2, …,euD)。

(3)设置初始迭代数t=0。

(4)确定涡流搜索空间的初始半径。初始均方差σ0也可以看作在二维优化问题中涡流外圈的初始半径r0，即r0≈σ0，σ0= maxelj+mineuj/2。算法搜索初始阶段，弱化局部性是必要的，所以初始半径r0可以选择一个较大的值,因此，初始步骤通过设置大半径的最外圈实现了搜索空间的全覆盖。

(5)产生候选解。初始候选解集Cts=S1,S2,…,Sn，t为迭代的次数，初始为0。通过以μ0为中心的高斯分布随机产生，n代表候选解集中解的个数。高斯分布的一般形式为

其中，x为D维随机向量；μ为D维样本均值(涡流中心)向量；Σ为协方差矩阵，Σ=σ2I；σ2为高斯分布的方差；I为D维单位矩阵。

(6)候选解的超边界处理。候选解必须在搜索空间边界内才能被选择，超出边界范围的解可以通过下式进行调整变换进入到边界内：

(9)

Δ=euj-elj

式中，Skj为第k组候选解集中第j维的备选解；r为一符合均匀分布的随机数。

(7)对高斯分布产生的n个解进行目标函数值计算，选出该代中的目标值最优解O，以及O对应的待优化序列最优解S′。

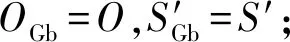
(9)若t小于最大迭代数gmax，则令t←t+1，否则，执行步骤(13)。

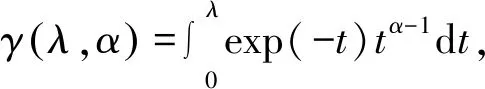
rt≈σt=σ0γ(λ,α)/λ

(12)令μ=μt，r=rt，执行步骤(5)，进入下一次迭代。

由以上可得，堆垛机调度优化的涡流搜索算法流程见图4。

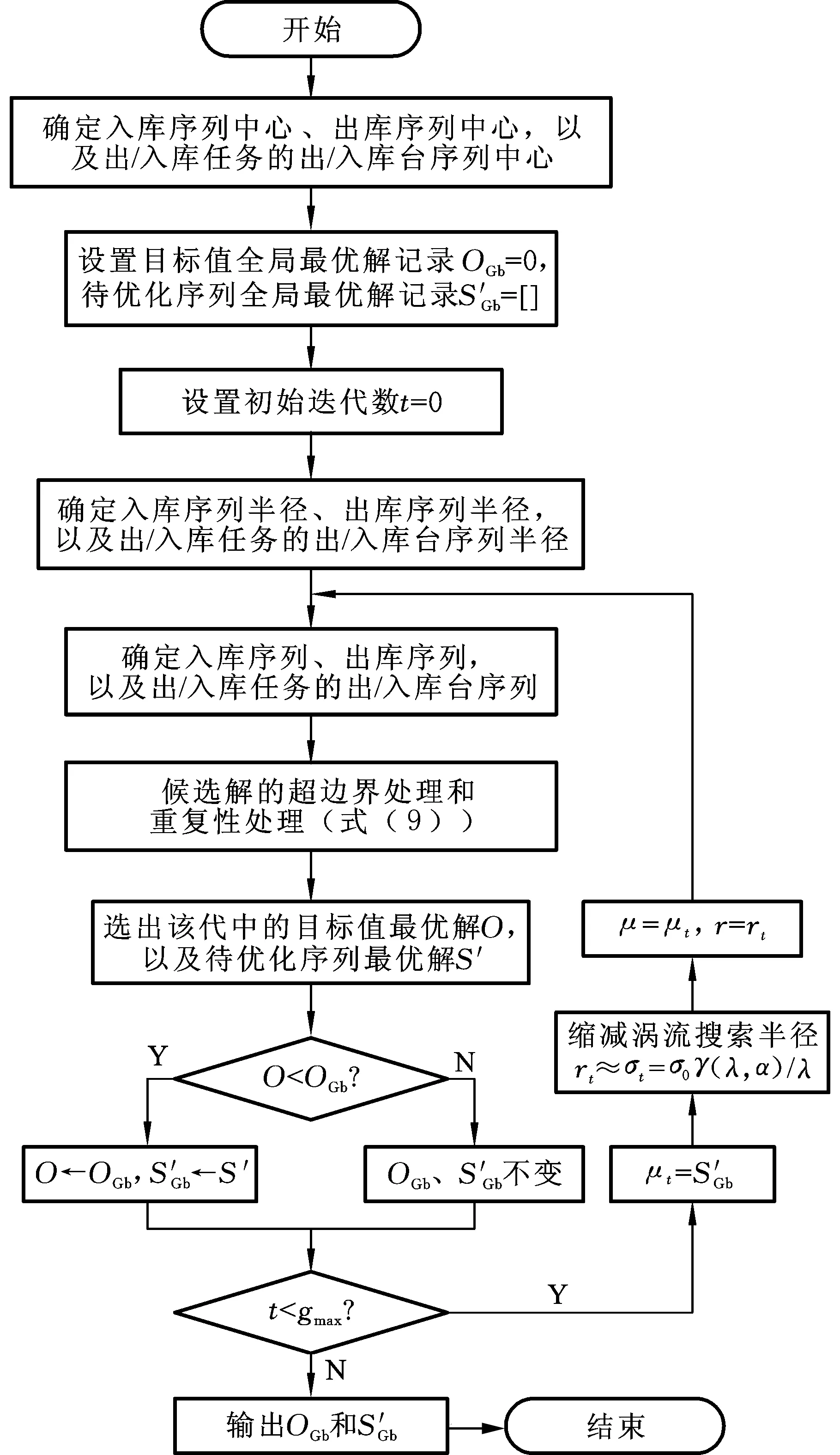
图4 堆垛机调度优化的涡流搜索算法流程Fig.4 Optimization process of vortex search algorithm for stacker crane scheduling

以所建立的堆垛机调度模型为基础，以堆垛机完成一出/入库作业订单时间最短为目标，通过运用涡流搜索算法，最终获得出/入库任务的作业序列以及各任务所对应的出/入库台。

4 仿真验证

以某企业实际使用的自动化立体仓库为研究对象，验证所建立的调度模型的适用性和涡流搜索算法的有效性。该仓库采用固定货架挑选模式，当1个出/入库作业订单指令被传送至堆垛机控制台时，如何调度堆垛机在最短时间内完成所有出/入库任务是衡量其仓储能力的唯一标准。该立体仓库由1条巷道、成组的2排货架、1台堆垛机、货物缓冲区、外部输送系统和货物分拣台组成，每排货架为12层、80列，共有12×80×2=1 920个货位用于货物存储。出/入库台共有2个，分布在巷道两端，均可用于货物的出库和入库，两端出/入库台的坐标分别为(1,0)和(1,81)。堆垛机在作业过程中1次最多只能装载1件货物，固定货架的每个货位尺寸相同，且货架中每个货位也只能存放1件货物。该立体仓库各项指标参数见表1，在实际生产中，某批出/入库作业订单的出/入库任务序列和对应货位坐标见表2。

表1 该立体仓库各项指标参数

表2 出/入库作业订单的任务序列和对应货位坐标

针对该出/入库作业订单，采用涡流搜索(VS)算法对其进行优化求解，同时以遗传算法(GA)和混合粒子群优化(CPSO)算法为基准，验证VS算法较GA算法和CPSO算法在解决两端式自动化立体仓库出/入库调度问题方面的优越性。三种算法的各项仿真参数设置如下：VS算法迭代次数为200，候选解个数为1 000；GA算法迭代次数为200，初始化染色体数为1 000，交叉算子为0.95，变异算子为0.05；CPSO算法迭代次数为200，初始化粒子数为1 000。

运用所建立的堆垛机调度模型对该出/入库作业订单任务进行优化仿真，堆垛机调度执行时间的优化曲线如图5所示。

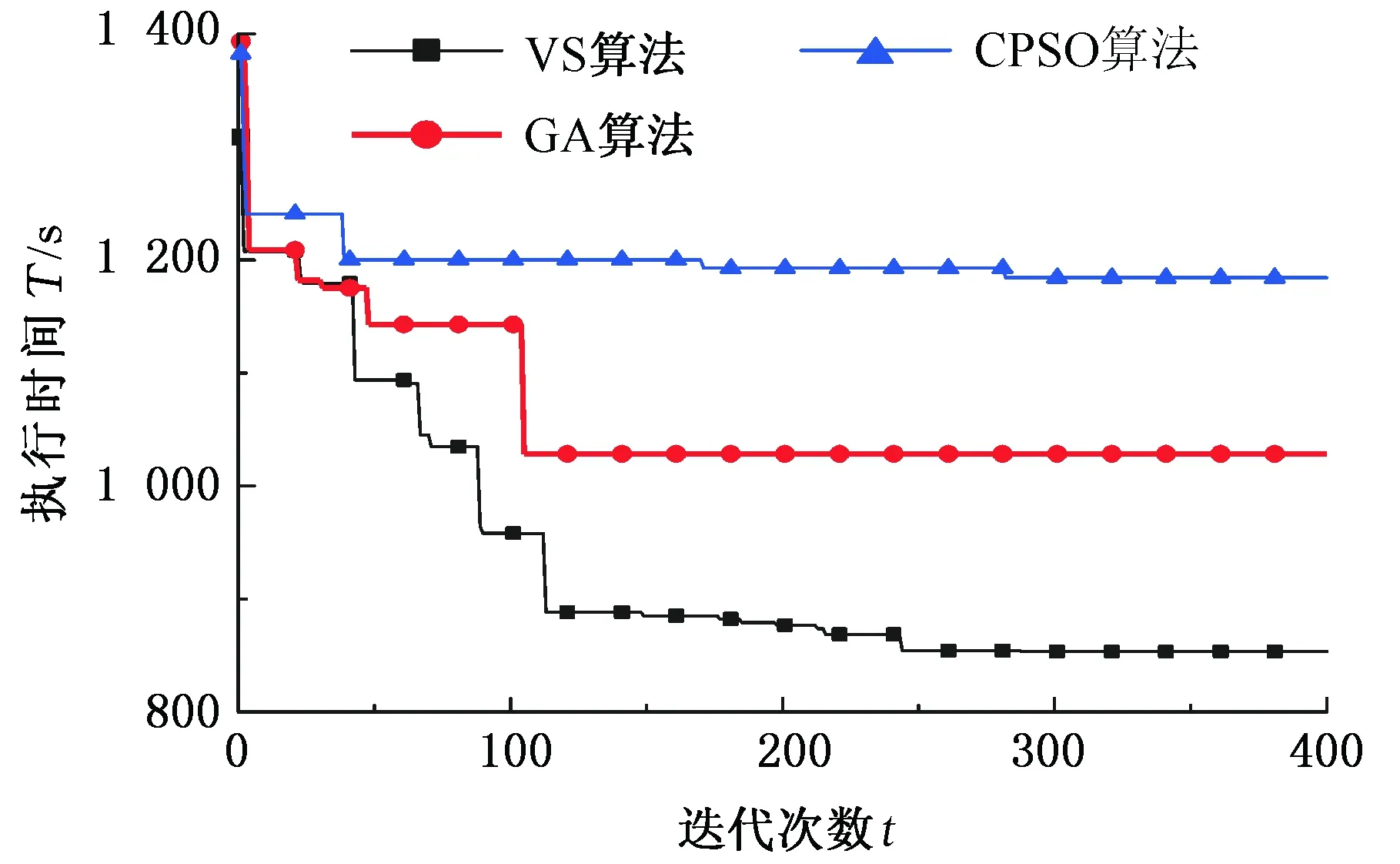
图5 堆垛机执行时间优化曲线Fig.5 Optimization curve of stacker execution time

由图5可知，堆垛机执行该出/入库订单任务所需要的时间随着迭代次数的增加，逐渐缩短，与GA算法和CPSO算法相比，VS算法在解的质量方面表现更优。VS算法在迭代至288代时达到最优，此时堆垛机的调度执行时间为853.5 s，而在实际工况下，堆垛机执行该任务订单所需要的实际时间为1 324 s，优化后,堆垛机的调度执行效率提高了35.5%。

优化后，堆垛机调度运行的最短时间所对应的出/入库任务序列以及与其对应的出/入库台序列即为最优序列，见表3。

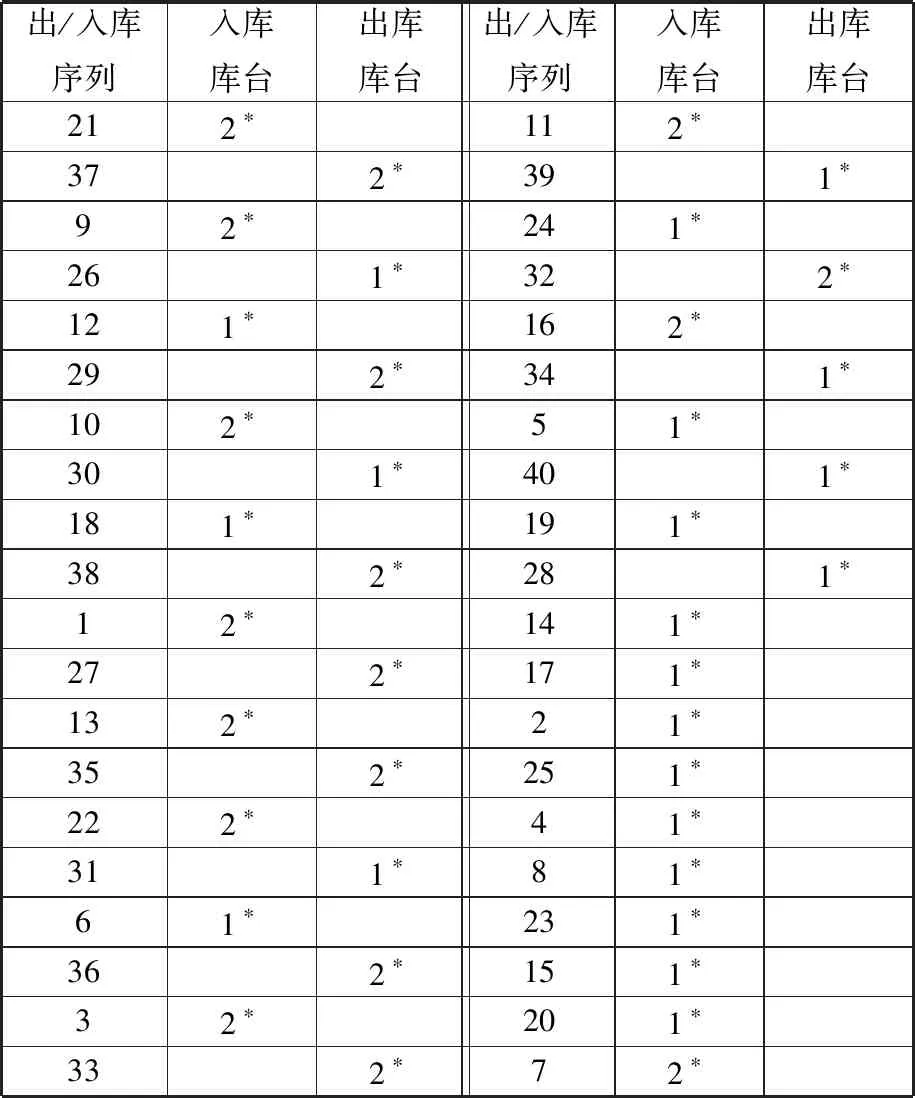
表3 出/入库任务序列以及与其对应的出/入库台序列

注：表中的1*、2*分别代表左端出/入库台和右端出/入库台。 在求得堆垛机的最优调度路径后，可知堆垛机的运行序列：

2*→21→37→2*→9→26→1*→12→29→2*→10→30→1*→18→38→2*→1→27→2*→13→35→2*→22→31→1*→6→36→2*→3→33→2*→11→39→1*→24→32→2*→16→34→1*→5→40→1*→19→28→1*→14→1*→17→1*→2→1*→25→2*→4→1*→8→1*→23→1*→15→1*→20→2*→7→2*。

综上所述，本文建立的堆垛机调度模型适用于两端式布局的立体仓库，通过VS算法优化求解得到了堆垛机路径调度的最优解，并与GA算法和CPSO算法进行比较，验证了VS优化算法的有效性和优越性。

5 结 论

(1)在分析两端式仓库布局结构形式和作业特点的情况下，提出了适用于两端式仓库布局下堆垛机的SC和DC作业方式。

(2)在两端式仓库布局下，以堆垛机执行出/入库任务序列所需的总时间为评价标准，对堆垛机调度路径进行建模。建立了适用于两端式仓库布局下的堆垛机调度路径模型，将入库任务和出库任务组合起来考虑，形成DC任务和SC任务，减少了堆垛机的往返次数，并将出/入库货物的出/入库台选择也纳入调度路径的优化模型之中，使得调度优化更加有效。

(3)针对GA算法、CPSO算法等智能算法需要迭代次数较大才能找到近似最优解，且容易陷入局部最小、收敛效率低等缺点，利用涡流搜索算法对所建立的堆垛机调度路径模型进行优化求解，在算法迭代的过程中嵌入小生境技术，得到最优出/入库任务序列以及货物对应的出/入库台序列。通过实例仿真，并将仿真结果与GA算法和CPSO算法的仿真结果进行比较，验证了所建立的堆垛机调度路径模型的正确性，以及涡流搜索算法在优化堆垛机调度路径方面的适用性和优越性。