镁合金非对称应力载荷下的低周疲劳损伤演化和寿命预测

陈 凌 张贤明 刘 飞 欧阳平 贾艳艳

1.重庆工商大学废油资源化技术与装备工程研究中心，重庆，400067 2.重庆大学机械工程博士后科研流动工作站，重庆，400044 3.重庆工商大学制造装备机构设计与控制重庆市重点实验室，重庆，400067

0 引言

近年来，随着镁合金在汽车、航空航天等领域的大量应用，镁合金的疲劳研究得到了广泛的关注。目前，主要的研究集中在材料的低、高周疲劳行为[1-3]及稀土元素、热处理等工艺对材料的性能强化[4-6]等方面，对镁合金非对称载荷加载的疲劳研究较少。实际工况中，镁合金部件多承受非对称循环应力载荷的作用，除疲劳载荷外，部件还承受平均应力导致的棘轮效应的影响。针对镁合金非对称应力载荷下的疲劳，LIN等[7-10]的研究主要集中在材料非对称循环应力载荷下的棘轮效应及其影响因素，缺乏相应工况下的疲劳损伤演化和寿命预测的研究。

材料的低周疲劳损伤演化和寿命预测是相应零部件强度设计、优化和安全评估的基础，目前关于镁合金的低周疲劳损伤演化和寿命预测的研究较少，主要以经典的Miner线性累积损伤理论、Manson-Coffin公式、Basquin公式及其在此基础上的修正[11-14]为主，缺乏对镁合金非对称载荷加载的低周疲劳损伤演化和寿命预测的研究。

笔者在室温环境下，通过铸造镁合金AZ91D和变形镁合金AZ31B非对称应力载荷的低周疲劳试验，基于连续损伤力学，分别选取弹性模量、等效模量、总应变能密度以及平均应变的变化作为损伤变量，对镁合金非对称应力载荷下的低周疲劳损伤演化进行分析，建立了相应的低周疲劳寿命预测模型。为验证各损伤变量对应的寿命模型预测效果，选取各寿命段采样数据，用上述模型进行了镁合金非对称应力载荷下的低周疲劳寿命预测。

1 低周疲劳损伤演化和寿命预测

1.1 损伤变量与低周疲劳损伤演化

损伤变量是一种用于描述材料内部损伤状态变化及其对材料力学作用影响的内部状态变量。合适的损伤变量可以反映材料的低周疲劳损伤演化过程。对于应力控制的低周疲劳来说，通常将弹性模量E的变化作为损伤变量：

DE=1-EN/E0

(1)

式中，DE为以弹性模量的变化为损伤变量定义的材料损伤；EN为材料循环过程中的弹性模量；E0为材料初始无损伤时的弹性模量。

在式(1)的基础上，用等效模量Eeq代替弹性模量，可得损伤变量：

DE,eq=1-Eeq,N/Eeq,0

(2)

Eeq=(σmax-σmin)/(εmax-εmin)

(3)

式中，DE,eq为以等效模量的变化为损伤变量定义的材料损伤；Eeq,N为材料循环过程中的等效模量；Eeq,0为材料初始无损伤时的等效模量；σmax、σmin分别为每一循环过程中的最大应力和最小应力；εmax、εmin分别为每一循环过程中的最大应变和最小应变。

选择弹性模量或等效模量的变化作为损伤变量，对循环软化的材料较为适用。对于循环硬化的材料，在循环初始快速硬化阶段，选择弹性模量或等效模量的变化反映疲劳损伤的效果较差。对于非对称应力加载下的疲劳损伤，弹性模量或等效模量不能很好地反映平均应力导致的棘轮效应的影响。

为反映非对称应力加载过程中棘轮效应以及累积塑性变形对疲劳损伤的影响，选择总应变能密度ΔWt或平均应变εm的变化作为损伤变量：

DΔWt=1-ΔWt,0/ΔWt,N

(4)

Dεm=εm,N/εm,f

(5)

式中，DΔWt为以总应变能密度的变化为损伤变量定义的材料损伤；Dεm为以平均应变的变化为损伤变量定义的材料损伤；ΔWt，0为材料初始无损伤时的总应变能密度；ΔWt,N为材料循环过程中的总应变能密度；εm,N为材料循环过程中的平均应变；εm,f为材料断裂时的平均应变。

对于式(4)所定义的损伤变量，总应变能密度为弹性应变能密度和塑性应变能密度之和[15]：

ΔWt=ΔWe+ΔWp

(6)

(7)

其中，ΔWe为弹性应变能密度，用来反映非对称载荷下平均应力的影响；|Δσ|为名义应力最大值与最小值的差值；σm为平均应力；ΔWp为塑性应变能密度，用来反映累积塑性变形的影响，由循环过程中迟滞徊线所围面积得到。

材料初始无损伤时的塑性累积为零，因此，对于式(4)所定义的损伤变量，材料初始无损伤时的总应变能密度取弹性应变能密度。

式(5)定义的损伤变量以平均应变的变化来综合反映棘轮效应和塑性变形的累积，物理意义明确，同时测量较为容易。

通过上述各式定义的损伤变量，可计算得到各循环周次镁合金材料的材料损伤，通过材料损伤随循环周次的变化即可分析镁合金材料的低周疲劳损伤演化规律。

1.2 低周疲劳损伤及寿命预测模型

(8)

式中，D为材料损伤变量。

对损伤动力学方程(式(8))进行积分，积分上下限DN=0=D0，DN=Nf=1 ，可得材料的低周疲劳损伤模型：

D=1-(1-D0)(1-N/Nf)k

(9)

式中，D0为材料常数，代表材料初始循环时的损伤值。

在实际的疲劳试验中，疲劳试验机采用渐进保护式加载，即加载幅度以Δσ/4、Δσ/2、3Δσ/4、Δσ的应力历程进行，因此，实际疲劳工况中材料初始循环的损伤除材料本身的初始损伤外，还包括前期加载幅度小于|Δσ|时造成的材料损伤。

在式(9)基础上，联立式(1)、式(2)、式(4)、式(5)，可得不同损伤变量下的低周疲劳预测寿命模型：

(10)

(11)

(12)

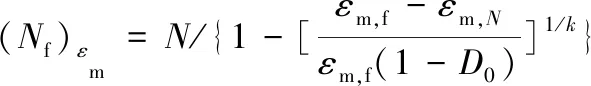
(13)

式中，(Nf)E、(Nf)E,eq、(Nf)ΔWt、(Nf)εm分别代表以弹性模量、等效模量、总应变能密度和平均应变的变化作损伤变量所得寿命预测模型的疲劳寿命。

基于式(10)～式(13)，根据循环周次和对应的弹性模量、等效模量、总应变能密度以及平均应变等疲劳参数，即可得到相应的疲劳寿命，进而考察不同损伤变量下基于材料低周疲劳损伤模型的寿命模型预测效果，为相应工况下镁合金材料的损伤评估和寿命预测提供理论依据。

2 试验结果及讨论

试验在电液伺服疲劳试验机上进行，试验温度为25 ℃，试验材料为铸造镁合金AZ91D和变形镁合金AZ31B，试验材料室温下的力学性能和化学成分见文献[15]。试验用疲劳试样为光滑圆棒试样，参照GB/T 15248-2008[18]进行制作。试验控制模式为应力控制，控制波形为三角波，采用脉动循环(应力比为0)，加载频率为3～5 Hz。具体的试验数据和试验结果见表1、表2，试验装置和试样尺寸见图1，其中，σa为名义应力幅，Δσ为各义应力范围。

图1 疲劳试验装置及试样Fig.1 Equipment and specimen in fatigue experiments

表1 铸造镁合金AZ91D低周疲劳试验数据及结果(25 ℃)

表2 变形镁合金AZ31B低周疲劳试验数据及结果(25 ℃)

图2、图3分别为铸造镁合金AZ91D和变形镁合金AZ31B的弹性模量、等效模量随寿命分数N/Nf的变化曲线，其中，弹性模量通过材料每循环应力-应变曲线(迟滞徊线)的弹性段获得，等效模量的计算公式为式(3)。由图2、图3可知：①铸造镁合金AZ91D的弹性模量、等效模量随循环周次的增加而增大，材料的弹性模量、等效模量在循环后期才出现下降趋势，表明铸造镁合金AZ91D在循环过程中出现循环硬化；当循环周次接近疲劳寿命时，材料才出现软化趋势。②变形镁合金AZ31B的弹性模量、等效模量在初始循环阶段随循环周次的增加而降低，之后随循环周次的增加而增大；材料的弹性模量、等效模量在循环后期才出现下降趋势，表明变形镁合金AZ31B经初始阶段的循环软化后，在循环过程中呈现循环硬化，当循环周次接近疲劳寿命时，材料才出现软化趋势。

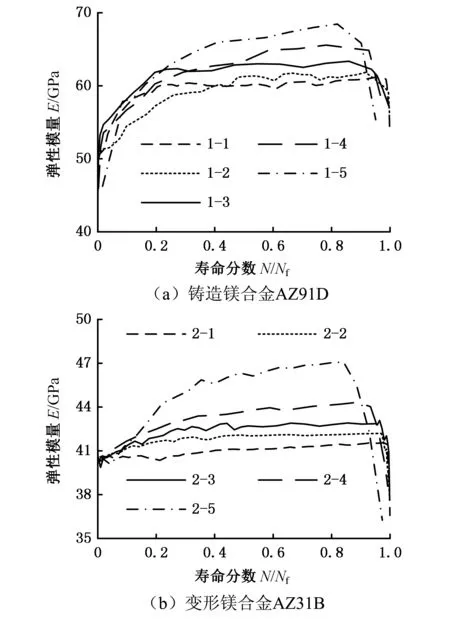
图2 镁合金弹性模量随寿命分数变化Fig.2 Change of elastic modulus of magnesium alloys with life fraction

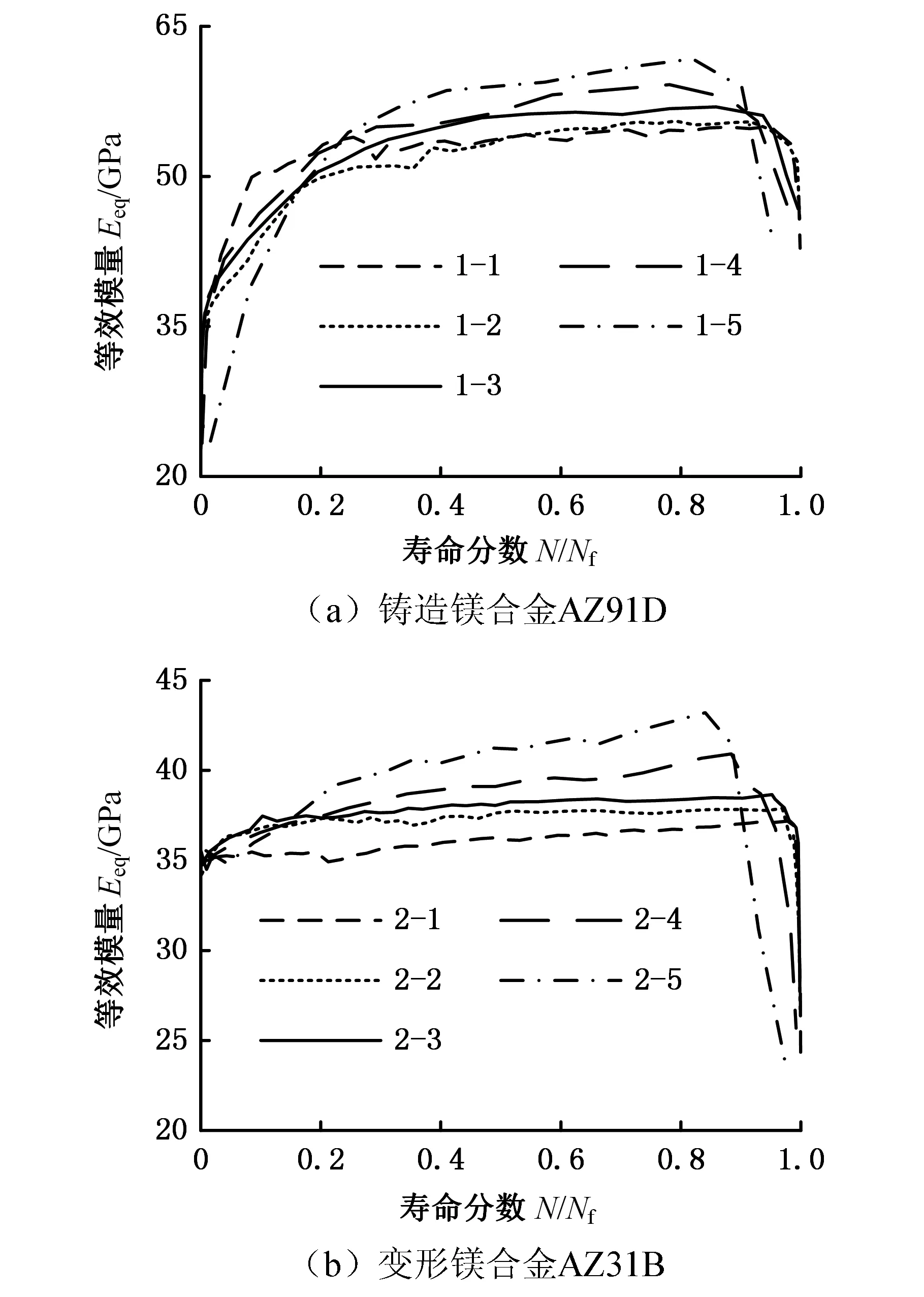
图3 镁合金等效模量随寿命分数变化Fig.3 Change of equivalent modulus of magnesium alloys with life fraction

由式(1)、式(2)可知，将弹性模量或等效模量的变化作为损伤变量，对循环硬化阶段的材料损伤进行描述时会出现损伤为负的情况，不能反映材料的损伤情况。AZ91D、AZ31B在大部分循环阶段内均呈现循环硬化，因此，利用弹性模量或等效模量的变化作为损伤变量不适用于材料AZ91D、AZ31B非对称应力载荷下的低周疲劳损伤描述，相对应的寿命预测模型也不适用于材料非对称应力载荷下的低周疲劳寿命预测。

图4、图5分别为铸造镁合金AZ91D和变形镁合金AZ31B的总应变能密度、平均应变随寿命分数N/Nf的变化曲线，其中，总应变能密度的计算公式为式(6)。由图4、图5可知：铸造镁合金AZ91D和变形镁合金AZ31B的总应变能密度、平均应变随循环周次的增加而增大，当循环周次接近疲劳寿命时，总应变能密度和平均应变的增大趋势明显提高。总应变能密度和平均应变的变化趋势与材料的损伤演化过程较为一致，即材料损伤随着循环周次的增加逐渐累积，当损伤的累积到达一定程度后导致材料快速失效。

图4 镁合金总应变能密度随寿命分数变化图Fig.4 Change of total strain energy density of magnesium alloys with life fraction

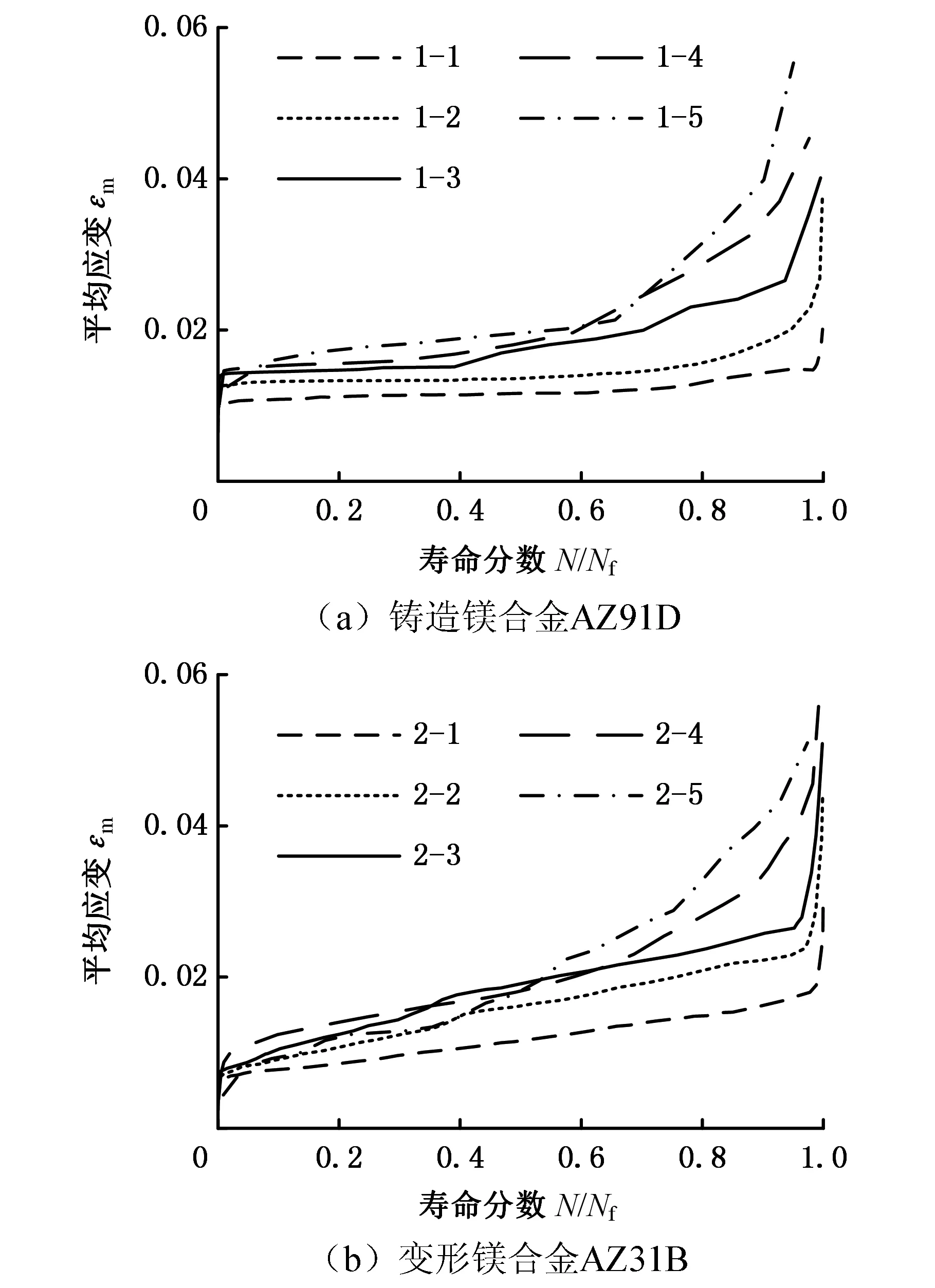
图5 镁合金平均应变随寿命分数变化图Fig.5 Change of mean strain of magnesium alloys with life fraction

根据式(4)、式(5)定义的损伤变量公式，分别计算不同寿命分数下以总应变能密度及平均应变的变化作为损伤变量时的材料损伤，可得铸造镁合金AZ91D和变形镁合金AZ31B非对称应力载荷下的低周疲劳损伤变化曲线，如图6、图7所示。由图6、图7可知，以总应变能密度及平均应变的变化作为损伤变量时，材料AZ91D、AZ31B的疲劳损伤随寿命分数的变化具有典型的连续材料疲劳损伤演化特征，即材料的疲劳损伤随循环周次的增加而增加，在循环的稳定阶段，疲劳损伤的增加速率较小且变化不大，当循环周次接近疲劳寿命时，材料的损伤累积接近材料失效的临界值，材料的疲劳损伤迅速增加，并快速导致材料失效。因此，用总应变能密度或平均应变的变化作为损伤变量来描述镁合金非对称应力载荷下的低周疲劳损伤演化是可行的。

以式(4)、式(5)定义的总应变能密度及平均应变的变化作为损伤变量，对式(9)所示的损伤模型进行拟合，可得铸造镁合金AZ91D和变形镁合金AZ31B各工况下的低周疲劳损伤模型，图8为代表性拟合图，拟合结果见表1、表2。

图6 以DΔWt=1-ΔWt，0/ΔWt，N为损伤变量的镁合金低周疲劳损伤变化曲线Fig.6 Low cycle fatigue damage change curves of magnesium alloys by defining damage variable as DΔWt=1-ΔWt，0/ΔWt，N

图7 以Dεm=εm，N/εm，f为损伤变量的镁合金低周疲劳损伤变化曲线Fig.7 Low cycle fatigue damage change curves of magnesium alloys by defining damage variable as Dεm=εm，N/εm，f

图8 镁合金低周疲劳损伤模型拟合图Fig.8 Fitting curves of low cycle fatigue damage models for magnesium alloys

由图8可以看出：选取总应变能密度或平均应变的变化作为损伤变量，基于式(9)所示损伤模型所得的损伤曲线与损伤点较符合。由于变形镁合金的组织结构相对于铸造镁合金更为致密、均匀，对连续损伤力学理论的符合程度更好，因此，变形镁合金AZ31B的损伤模型拟合曲线与损伤点的符合程度较铸造镁合金AZ91D好。另外，相较于总应变能密度，选取平均应变的变化作为损伤变量拟合所得损伤曲线与实测损伤点的符合程度更好。

将表1、表2所得损伤模型的材料常数k和初始损伤D0代入式(12)、式(13)，即可得到以总应变能密度及平均应变的变化为损伤变量的低周疲劳寿命预测模型。分别选取表1、表2中试验试样中1/4寿命分数 (Nf/4)、1/2寿命分数(Nf/2)和3/4寿命分数(3Nf/4)附近的采样点的循环周次及相应的总应变能密度和平均应变，利用式(12)、式(13)所示模型进行材料疲劳寿命的预测，预测效果如图9所示。由图9可知：①以总应变能密度或平均应变的变化作为损伤变量时，低周疲劳寿命预测模型均具有较好的预测效果，所有的寿命预测结果在2倍误差带以内，绝大部分的寿命预测结果在1.5倍误差带以内；②相较于总应变能密度，以平均应变的变化作为损伤变量的预测效果更好，更多的寿命预测结果处于1.5倍误差带以内。

图9 镁合金低周疲劳寿命预测效果图Fig.9 Low cycle fatigue prediction effects of magnesium alloys

由表1、表2可知：选取总应变能密度的变化作为损伤变量拟合所得的损伤模型材料常数k随载荷水平的变化规律较乱，选取平均应变的变化作为损伤变量拟合所得损伤模型的材料常数k随载荷水平的增加而增大。对于非对称载荷应力载荷下的低周疲劳来说，棘轮效应和塑性变形累积之间存在相互耦合，单纯采用总应变能密度不能很好地反映两者之间的耦合，导致损伤模型的材料常数k随载荷水平的变化规律较乱。棘轮效应、塑性变形累积及其相互耦合均会造成平均应变的增大，采用平均应变的变化作为损伤变量可以综合反映棘轮效应和塑性变形累积的影响，故损伤模型的材料常数k与载荷水平的对应关系较好。因此，相较于总应变能密度，选取平均应变的变化作为损伤变量所得的损伤曲线具有更好的代表性，可以较好地反映载荷对疲劳损伤的影响。

3 结论

(1)以总应变能密度或平均应变的变化作为损伤变量，能够反映非对称应力加载过程中棘轮效应以及累积塑性变形对疲劳损伤的影响，可用来描述镁合金非对称应力载荷下的低周疲劳损伤演化。受限于材料的循环特性，将弹性模量或等效模量的变化作为损伤变量，不合适描述镁合金非对称应力载荷下的低周疲劳损伤。

(2)基于连续损伤力学，用总应变能密度及平均应变的变化作为损伤变量表示损伤，建立了镁合金非对称应力载荷下的低周疲劳寿命预测模型。使用该模型进行了铸造镁合金AZ91D和变形镁合金AZ31B室温环境非对称应力载荷下的低周疲劳寿命预测，预测模型对不同寿命段的采样数据均具有较好的预测效果，所有的寿命预测结果在2倍误差带以内，绝大部分的寿命预测结果在1.5倍误差带以内。

(3)相较于总应变能密度，选取平均应变的变化作为损伤变量所得损伤曲线具有更好的代表性，可以较好地反映载荷对疲劳损伤的影响，与实测损伤点的符合程度更好，同时，以平均应变的变化作为损伤变量的低周疲劳寿命预测模型的预测效果也更好。