渐进多焦点镜片的设计与慢刀伺服车削

牛恒泰 康 敏,2 王兴盛 杨 军

1.南京农业大学工学院,南京，210031 2.南京农业大学灌云现代农业装备研究院，灌云，222200

0 引言

在实际应用中，渐进多焦点镜片需要根据配镜者眼睛的度数进行专门设计，故镜片面型设计方法是该领域的主要研究方向之一。渐进多焦点镜片的设计可按硬式设计和软式设计来进行分类，具体的设计方法包括WINTHROP[1]的方法、STEELE[2]的方法、HSU等的B样条方法[3]以及LOOS等的变分数值方法[4]等，传统的设计方法多为采用复变函数计算对曲面进行设计，其计算过程比较复杂。正是由于渐进多焦点曲面(progressive-addition lenses, PAL)面型的复杂性，其加工也面临着较大的挑战。目前的镜片加工方法主要包括注塑成形法和数控加工法。数控加工方法中，慢刀伺服车削技术具有较高的面型加工精度及加工效率，广泛应用于非球面光学元件的加工[5]，因此可将慢刀伺服车削技术用于渐进多焦点曲面的加工。

本文提出一种渐进多焦点曲面镜片的参数化几何建模的设计方法，它可以控制光焦度和像散变化、过渡区范围以及近视区远视区的面型和大小。该方法基于已知的曲率曲线的离散化处理，能够基于佩戴者的习惯和特点设计合适的渐进多焦点曲面镜片，通过改变近视区和远视区的尺寸和其他参数，如过渡区长度等，能够实现渐进多焦点曲面眼镜的便捷定制。此外，本文提出了一种离散形式曲面的刀触点生成方法，将慢刀伺服车削用于渐进多焦点曲面加工。

1 渐进多焦点曲面设计方法

渐进多焦点曲面(progressive-addition lenses, PAL)没有回转对称性，属于空间自由曲面，不能简单通过代数方程来表达,可以划分为四部分：近视区、远视区、过渡区和像散区，如图1所示。其中，近视区、远视区和中间过渡区为主要成像区。远视区的屈光度P为定值并且较小；远视区和近视区之间为过渡区，屈光度均匀变化，过渡区的屈光度的变化范围定义为ADD；近视区的屈光度也为定值，且屈光度相对较大，定义为P+ADD。

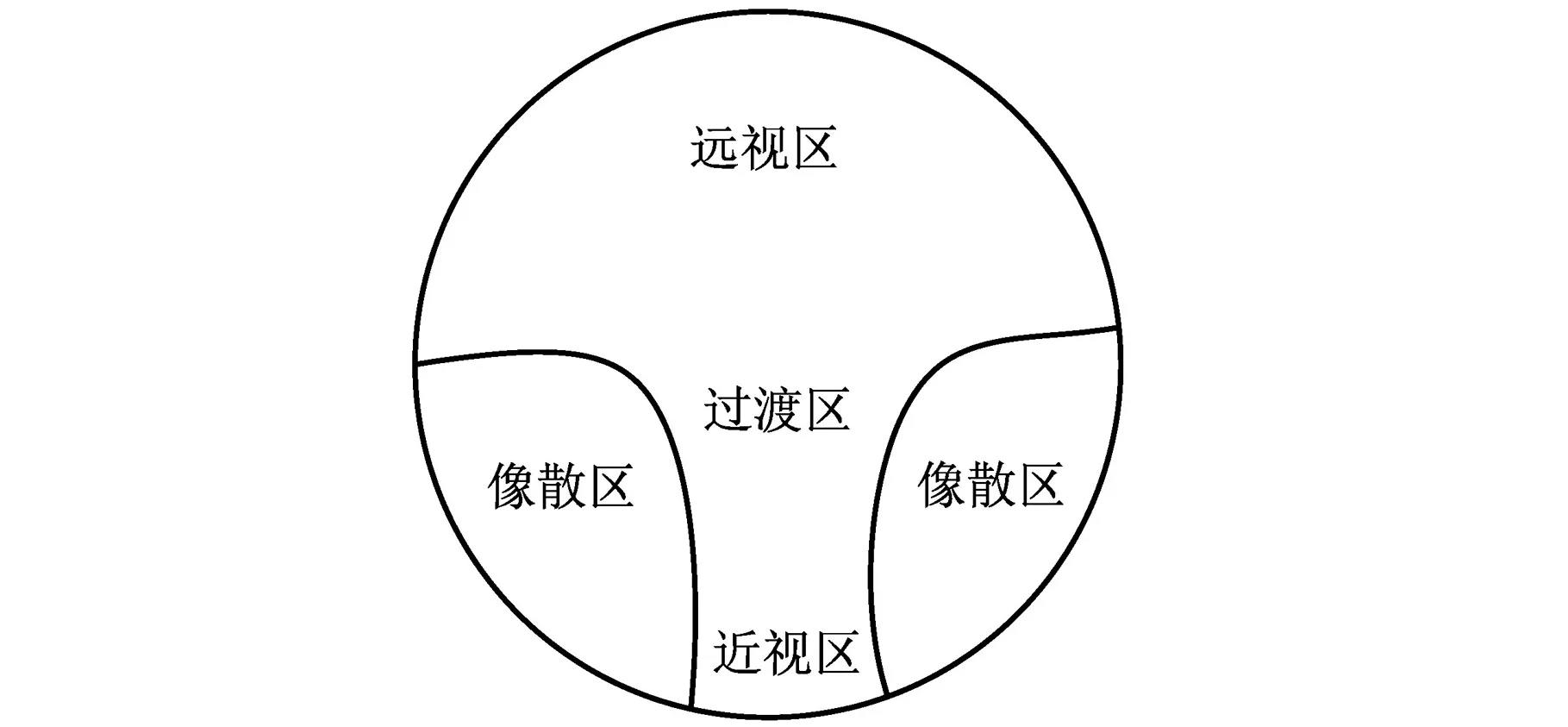
图1 渐进多焦点曲面镜片示意图Fig.1 Schematic diagram of progressive-addition lenses

本文的渐进多焦点曲面设计方法主要由曲面参数设置和曲面三维模型构建两部分组成。

1.1 曲面参数设置

渐进多焦点曲面设计建模过程涉及到的参数可以分为几何参数(远视区、近视区的尺寸和位置)和光学参数。主要几何参数见图2、表1。由过点D1、D2、D3的二次曲线围成的区域为远视区，由过点N1、N2、N3的二次曲线围成的区域为近视区。用于渐进多焦点曲面建模的光学参数见表2。

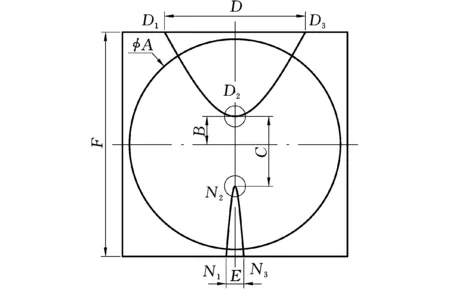
图2 几何参数定义Fig.2 Definition of geometric parameters

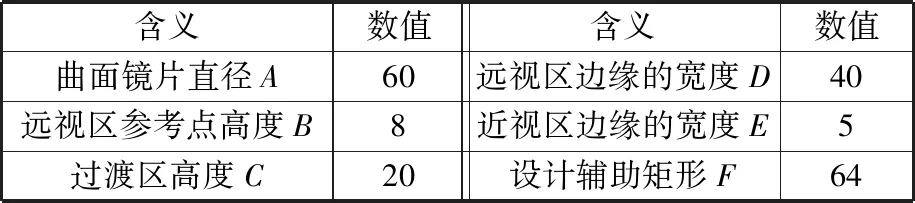
表1 几何参数的含义

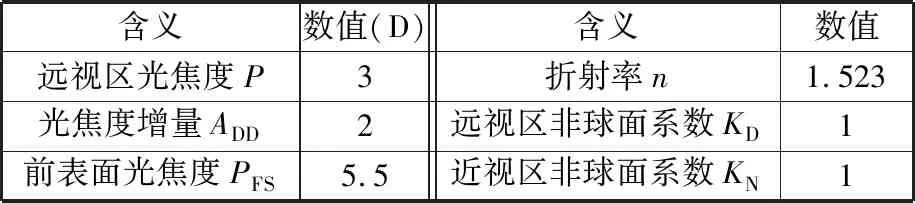
表2 光学参数的含义

注：D为光焦度的单位屈光度，1D=1 m-1

在透镜的折射率n=1.523情况下，已知中心厚度CT，就可得出前表面的曲率半径RF、远视区的曲率半径RD和近视区的曲率半径RN：

(1)

式中，cD、cN分别为远视区和近视区的曲率。

此外，通过改变前表面的曲率半径可以对近视区和远视区进行调整，也可以通过分别引入远视区和近视区的非球面系数KD和KN，以减少轴外散光。

1.2 曲面三维模型构建

光焦度和像散是评价渐进多焦点曲面镜片光学特性的2个主要参数。为确保中间过渡区的光焦度连续变化以及较低的像散，若要使像散为零，则该区域的主曲率必须相等[6]。镜片的光焦度与折射率以及表面平均曲率成比例，像散和两主曲率之差成比例。光焦度是衡量镜片偏折光线能力的物理量，单位为屈光度D(1D=1 m-1)，需要和佩戴人的眼睛度数匹配。屈光度与焦距成反比，焦距越小，屈光度越大；焦距越大，屈光度越小。像散单位同样为屈光度，但像散会造成成像不清晰，需要尽量避免[7]。故渐进多焦点曲面的最终设计目标可以概括为以下三点：①渐进多焦点曲面上各点的光焦度应该光滑过渡，没有像跳现象；②主要成像区的远视区和近视区的光焦度应该和理论值尽量一致；③渐进多焦点曲面上各点的像散应该尽量小，远视区、近视区和中间过渡区的像散最好为零，将镜片的像散尽量往像散区集中。

为满足上述条件，本文提出如下的建模过程。

(1)远视区模型构建。远视区为一中心在D2的非球面，可通过等距取点获得离散形式的曲面，每点(x，y)的z坐标为

(2)

(2)近视区模型构建。近视区为一中心在N2的非球面，可通过等距取点获得离散形式的曲面，每点(x，y)的z坐标为

(3)

图3中，两条白色抛物线划分了近视区、过渡区和远视区，上述步骤(1)、步骤(2)的建模结果即为图3所示的近视区和远视区。

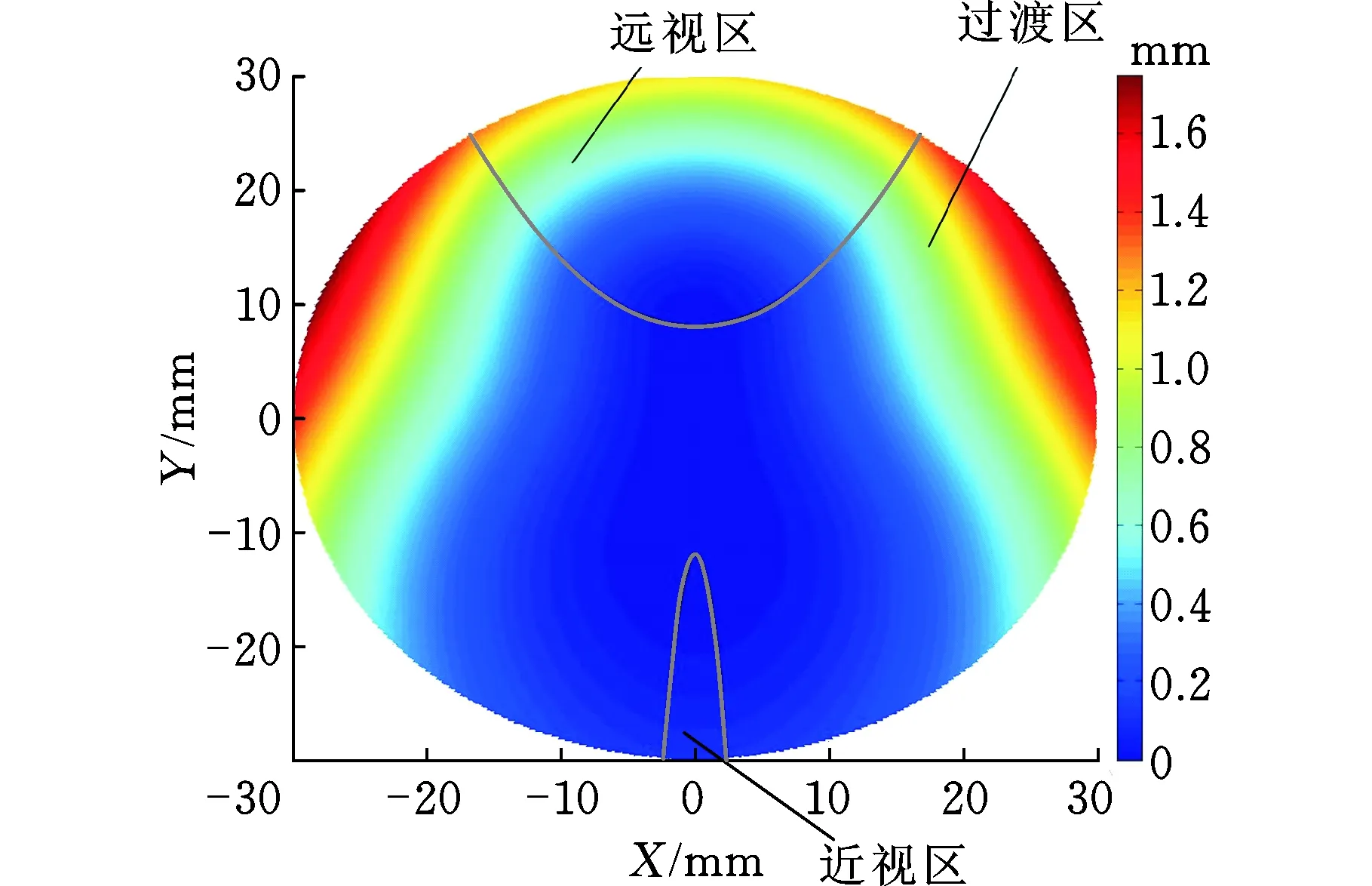
图3 渐进多焦点曲面模型Fig.3 PAL model

(3)过渡区模型构建。需先通过曲率设计构建一组二次曲线，通过在曲线上等距取点获得离散形式的面型。过渡区曲线上点(x，y)的z坐标为

(4)

式中，(Xci，Yci)是过渡区第i条曲线中点坐标，i=1，2，…，k；k为中间区域曲线的总数目；Rci是点(Xci，Yci)处曲率半径；Kci是点(Xci，Yci)处非球面系数。

过渡区的二次曲线由以下三点插值的方法构建：如图4所示，过渡区每条插值曲线需要先确定2个插值点然后进行插值，第一点通过下式

(5)

在点D2和点N2的连线上的等距取点得到。第二和第三点是通过特定半圆上的等弧长取点得到的，该半圆在远视区和近视区的边界曲线中间，圆心分别为D1N1和D3N3连线的中点。

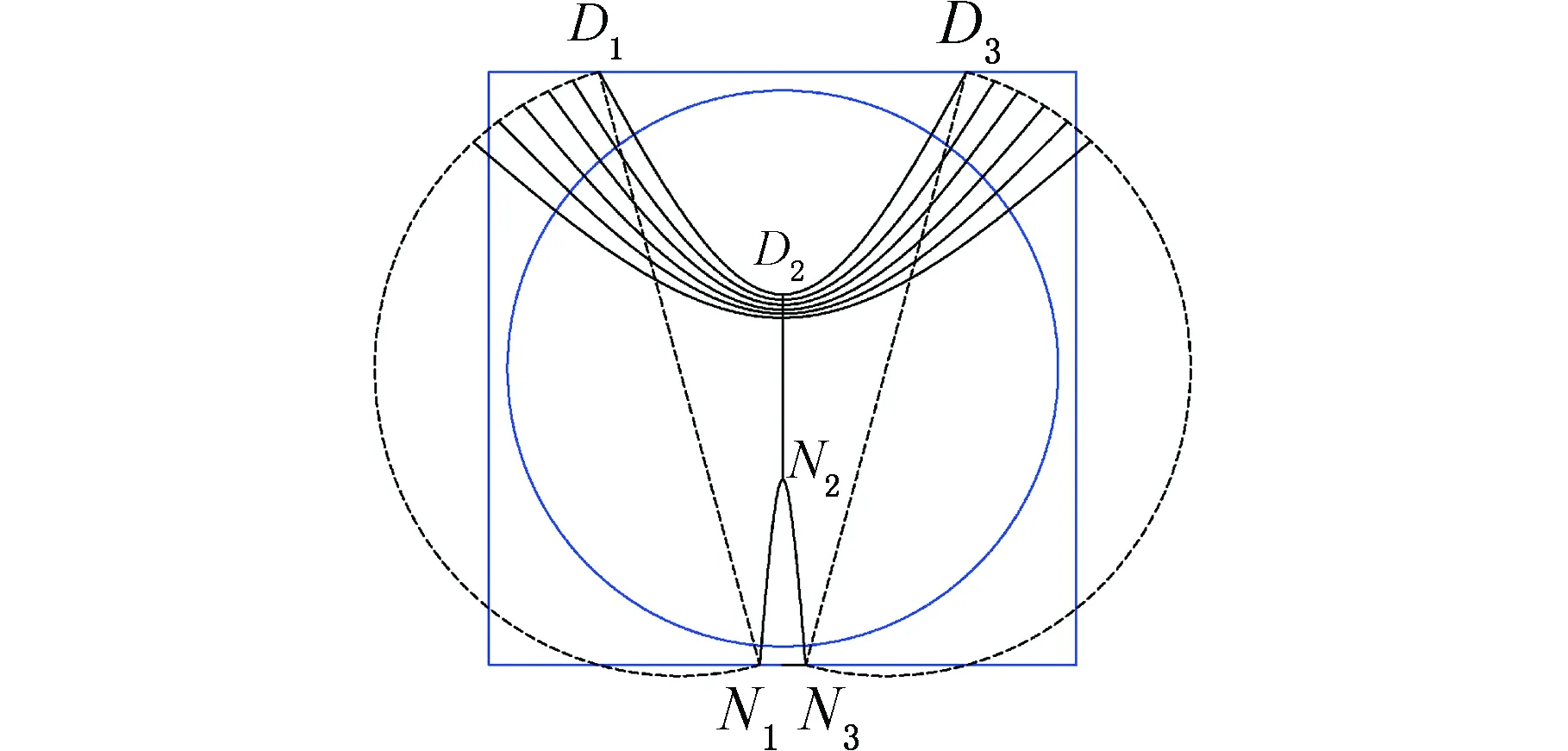
图4 过渡区曲线三点插值Fig.4 Curves interpolation of the intermediate area

为了获得连续的变化光学性能，过渡区的曲线的曲率必须严格控制，曲率ci为[8]

t=i/k

(6)

过渡区域的非球面系数为

Kci=-2(KN-KD)t3+3(KN-KD)t2+KD

(7)

过渡区曲线构建结果如图5所示。

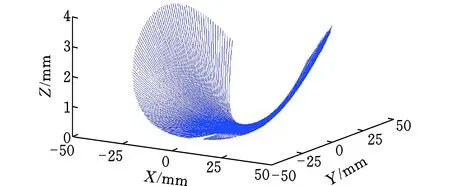
图5 过渡区曲线(k=101)Fig.5 Curves in intermediate area(k=101)

渐进多焦点曲面镜片设计的最后一个主要的步骤是将3个主要视觉区域进行组合，图3显示了3个区域组合后的结果。

2 曲面光学特性分析

渐进多焦点镜片的佩戴者主要靠主成像区进行成像，通过连续变化的光焦度实现全程空间清晰的视功能。一般情况下，渐进多焦点曲面镜片厚度较小，而且镜片一侧表面为渐进面，另一侧表面为各点曲率恒定的球面或非球面，因此渐进多焦点曲面镜片的光焦度P和像散S为

(8)

式中，n为镜片材料的折射率，n=1.53;K1、K2分别为曲面上一点的2个主曲率。

主曲率计算公式为

(9)

式中，e、f、g为曲面第一基本形式系数；L、M、N为曲面第二基本形式的系数[9]。

本文设计的渐进面为离散形式的曲面，在曲率计算时用差分代替了微分。

根据方程系数与根的关系，有

(10)

图6、图7所示为本文建模方法设计的渐进多焦点曲面与基底球面叠加后的光焦度与像散分布，可以看出，该曲面的光焦度过渡均匀且主成像区域的光焦度数值与设计一致，且主成像区域的像散为零，像散区域像散变化较小且不影响主成像区功能，符合设计要求。

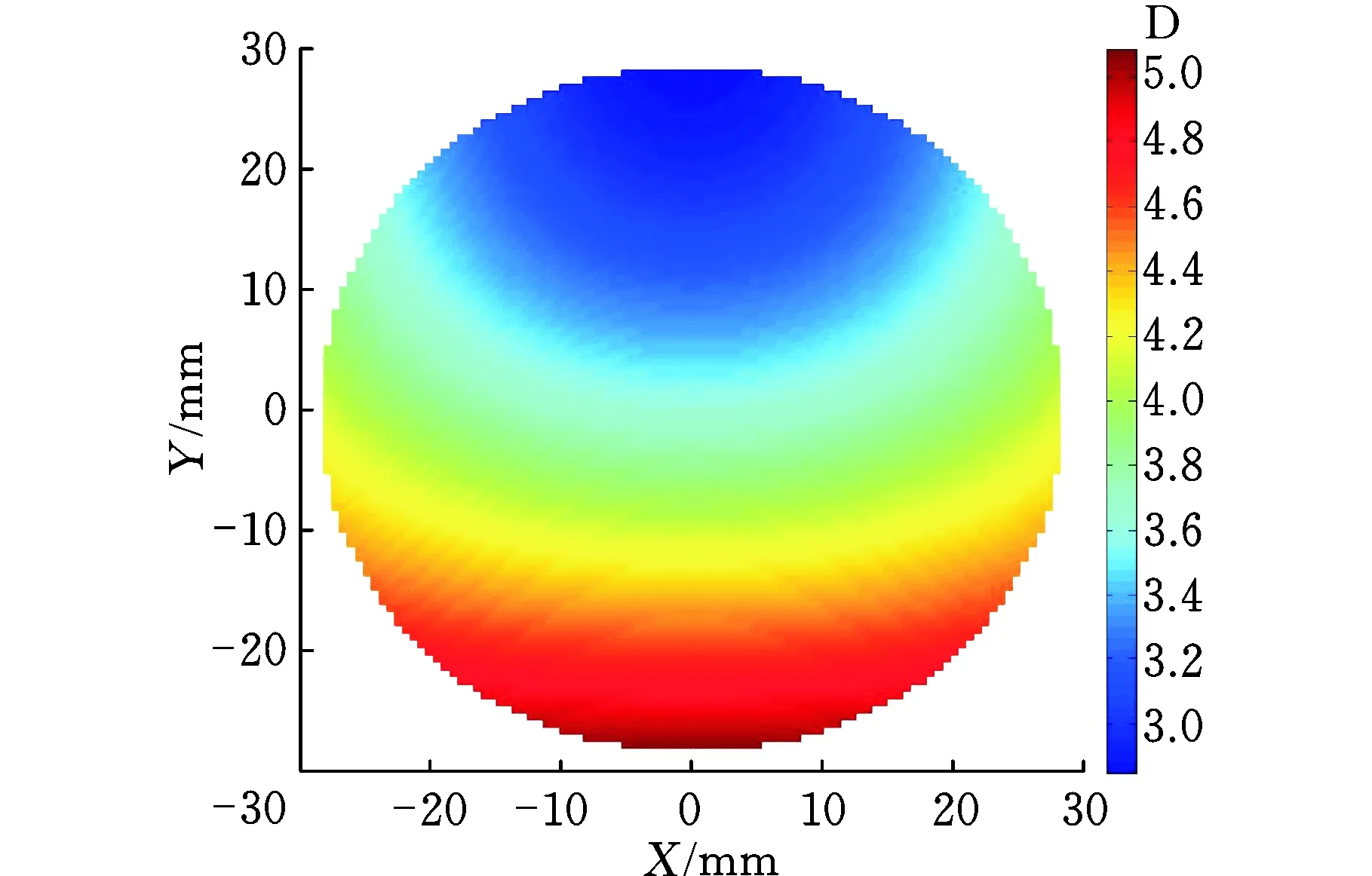
图6 光焦度分布Fig.6 Distribution of surface power

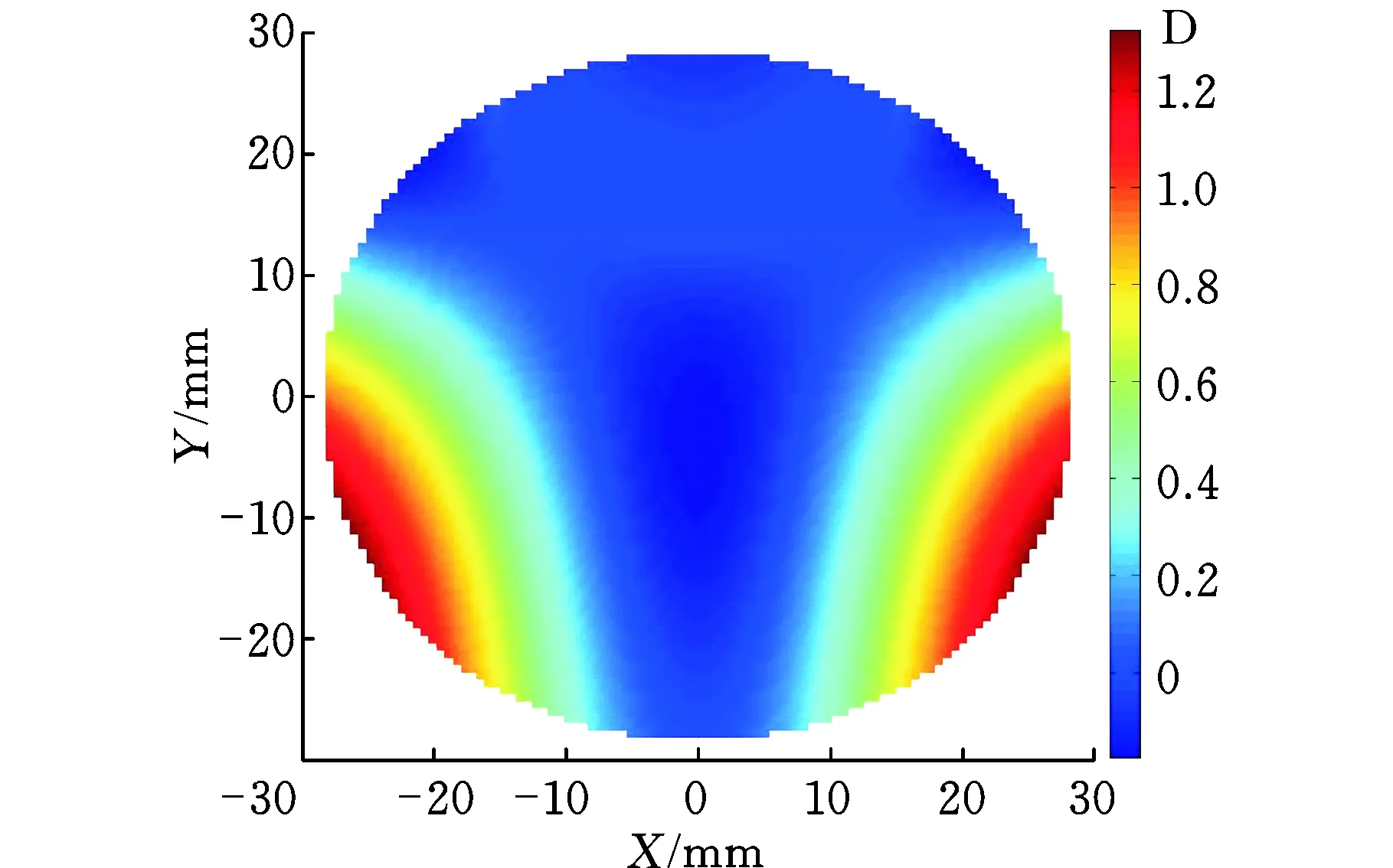
图7 像散分布Fig.7 Distribution of surface astigmatic power

进一步分析表明，过渡区的曲率方程(式(6))能够控制像散分布：当采用更高阶多项式时，像散的变化更为平滑，但像散的最大值将变得更大。过渡区曲率导数的值会影响像散的值，曲率导数减小，像散最大值将会增大。过渡区曲率导数与沿着过渡区的光焦度导数成正比，即与沿垂直方向的像散导数相关[7]。另外，设计参数中的ADD取值也会影响像散值，ADD增大，像散增大，最大像散的比值等于ADD之比；远视区或近视区面积增大，最大像散增加。

3 渐进多焦点曲面的慢刀伺服车削

慢刀伺服(slow tool servo，STS)车削技术是一种超精密车削方法，STS机床通过X、Z、C三轴联动可以高精度、高效率地加工包括渐进多焦点曲面在内的各类复杂自由曲面。STS车削过程中，刀具与加工曲面的切点称为刀触点，刀触点生成方法的优劣决定了刀具路径规划的精度，是曲面加工的关键。

3.1 刀触点生成

对于连续曲面，确定每一刀触点坐标(x,y)后，该点的z值可由曲面方程z=f(x,y)计算[10]，但对于离散形式的渐进多焦点曲面，每一刀触点坐标(x,y)与该点的z值并无明确的函数关系，因而不易通过方程计算。本文基于离散曲面的矩阵数据，通过对每个生成的刀触点坐标(x,y)处进行局部数据Zernike多项式拟合得到(x,y)处的z值，从而得到刀触点数据。如图11所示，按下式即可计算出XY平面的刀触点坐标：

(11)

式中，af为C轴每转一周刀具的X向进给量；θ=jΔθ，j=1，2，…，Q；Q为刀触点总数；Δθ为相邻两刀触点与原点连线投影至XY平面的夹角。

假设给定m×n阶离散曲面网格点数据矩阵，则只需要计算出每个刀触点(xc，yc)对应的zc值即可得到刀触点轨迹。图8中，工件半径R=20 mm，af=1 mm/r，Δθ=5°，Q=1 441。

图8 XY平面刀触点分布Fig.8 Cutting contact points in XY plane

首先，在XY平面上找出网格数据点中距第j个刀触点(xc，yc)最近的数据点(x,y)，图9中距离刀触点p最近的网格数据点为点5，取点5及附近的8个点数据对(xc，yc)进行局部拟合。

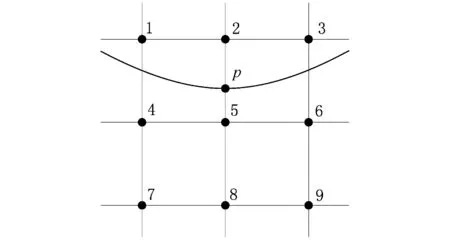
图9 局部拟合XY平面示意图Fig.9 Schematic diagram of local fitting in XY plane

Zernike多项式拥有良好的数学性能，有无穷多项而且均线性无关[11]，选用Zernike多项式对(xc，yc)进行局部区域拟合。Zernike多项式在直角坐标系中的表示为

(12)

式中，m为多项式项数；ai为多项式第i项系数；Zi为多项式第i项。

表3列出了极坐标系下和直角坐标系下的前6项具体表达式。可按这些数字式对数据点进行局部曲面拟合。如果离散曲面为细分曲面或者点集曲面，可类似地取刀触点周围点以及合适的多项式项数进行拟合。

使用Zernike多项式的前6项进行局部区域拟合，有

表3 Zernike多项式前6项表达式

上式可简记为

UA=Z

Ugh=Zh(xg,yg)

(13)

g=1，2，…，9h=0，1，…，5

式(21)中，方程个数大于未知数个数，因此是超定方程组，只有最小二乘解，若直接求解该方程组，可能因为阶数使最小二乘法形成的正则方程系数矩阵出现“病态”，而使得求解得到的Zernike多项式系数矩阵A不稳定。本文采用Householder方法对系数矩阵U进行QR分解[12]，将其正交三角化后再求最小二乘解，从而快速稳定地求出系数矩阵A，从而求出第j个刀触点(xc,yc)处的局部拟合曲面方程：

z=fi(x,y)

(14)

将刀触点(xc，yc)数据代入式(14)即可求得对应的zc。至此，通过给定m×n矩阵的离散曲面网格点数据就可以计算出第j个刀触点(xc，yc)对应的zc，从而得到所有刀触点的坐标。为获取该方法的拟合误差，将连续曲面离散为网格数据，通过该方法生成的Z坐标值与准确值之间的差值称为拟合误差，图10显示了拟合误差分布，可以看出，选取拟合点越多，越难反映局部面型，拟合误差越大，故本文取9个数据点进行拟合。

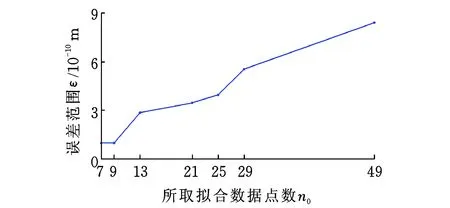
图10 误差范围与拟合数据点数关系Fig.10 Relation between error ranges and the number of fitting points

获取刀触点数据后，通过刀具形状补偿即可获得用以数控加工的刀位点数据，对刀位点进行轨迹插值后，可实现渐进面的STS车削。

3.2 实验及分析

本文利用实验室自主研制的STS数控车削实验装置进行加工实验，加工曲面为上文构造的远视区屈光度为3D、近视区屈光度为5D的渐进多焦点曲面，镜片直径d=60 mm，工件材料为树脂PMMA。实验加工艺参数如下：单圈横向进给速度af=0.5 mm/r，切削深度ap=0.01 mm，离散角Δθ=5°，刀尖圆弧半径Rt=0.2 mm，采用Z向刀具补偿。图11、图12所示为采用上述方法得到的刀触点及刀位点分布，图13为刀触点刀位点轨迹。

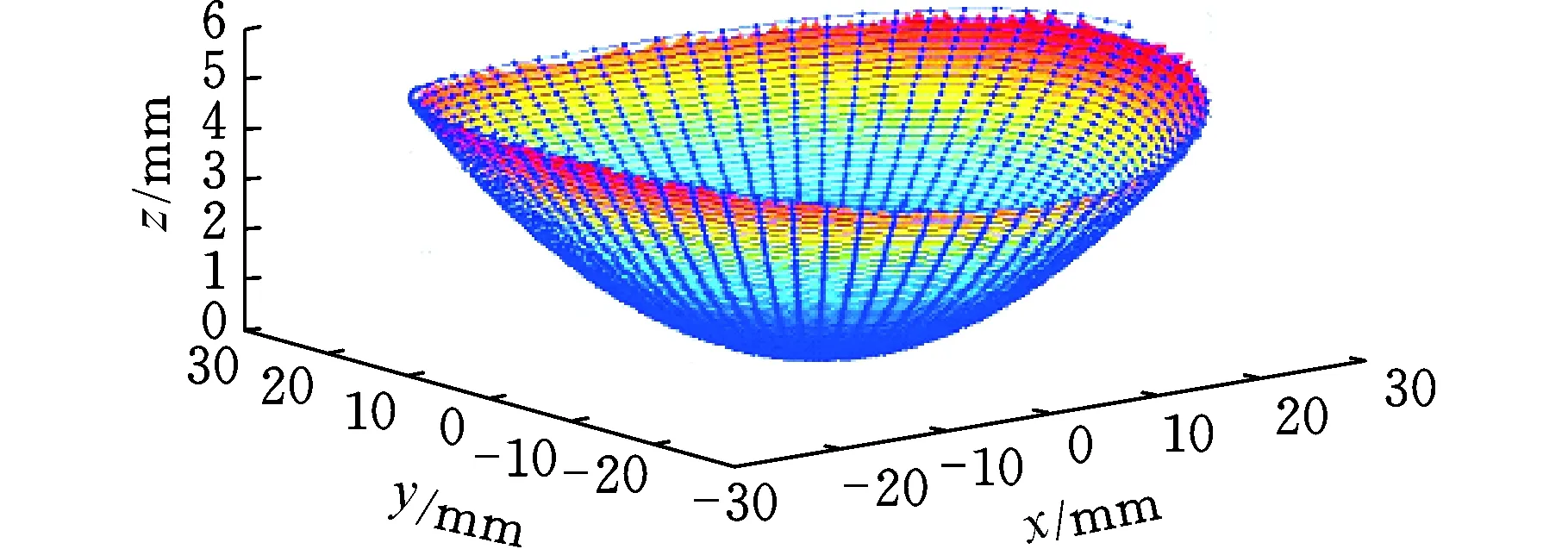
图11 渐进多焦点曲面刀触点分布Fig.11 Distribution of PAL cutting contact points

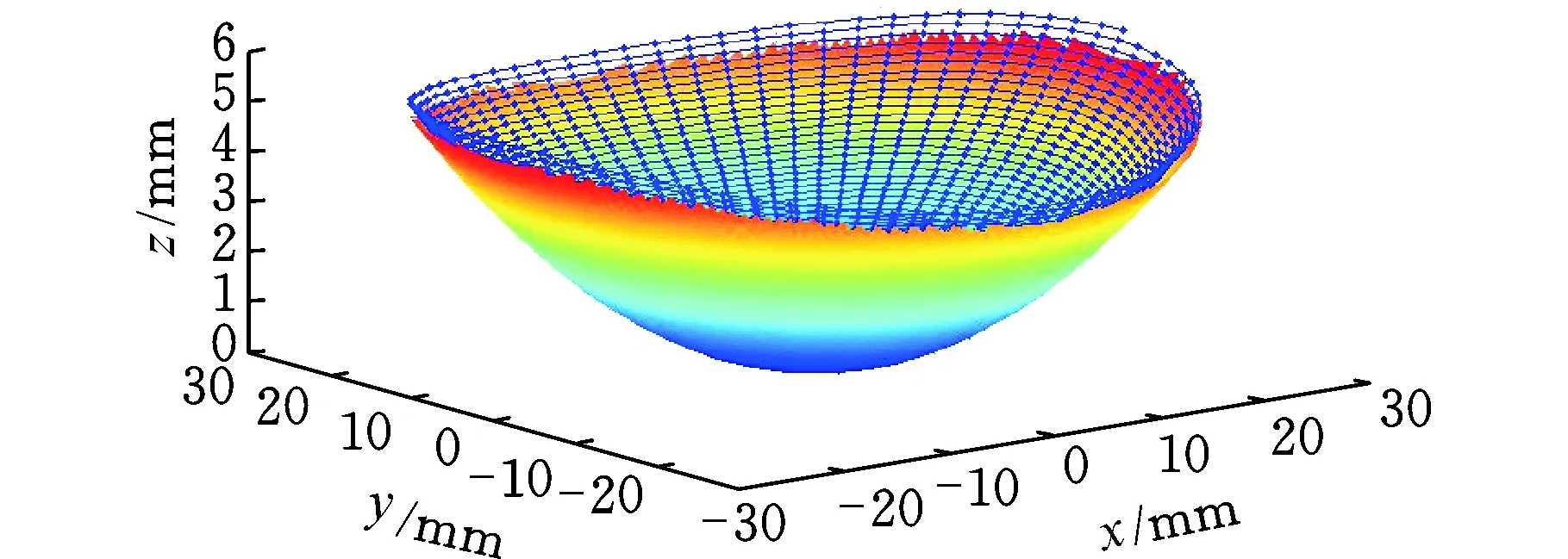
图12 渐进多焦点曲面刀位点分布Fig.12 Distribution of PAL cutting location points

图13 渐进多焦点曲面刀触点刀位点轨迹Fig.13 Trajectory of PAL cutting contact points and cutting location points

图14所示为加工得到的渐进多焦点曲面工件。采用OLS4100型激光共聚焦扫描显微镜对其表面粗糙度进行测量，其表面粗糙度Ra为0.283 μm。使用MQ686型三坐标测量仪测量加工得到的实际面型并将其与理论面型进行对比，面型误差分布如图15所示，面型误差为25 μm。

图14 渐进多焦点曲面工件Fig.14 Workpiece of PAL

图15 面型误差分布Fig.15 Distribution of surface error

4 结论

(1)提出的一种渐进多焦点曲面的参数化设计方法能较好地控制光焦度与像散分布，在不采用复变函数如积分或微分方程的情况下给出了类似的结果，避免了复杂的计算。该方法的主要优点是能够控制像散分布，改变远近视区的尺寸以及其他参数的尺寸，因此能够根据佩戴者的习惯实现高度定制化。

(2)将慢刀伺服车削技术用于渐进多焦点曲面的高精度加工。通过对离散数据进行局部Zernike多项式拟合，提出了一种针对包括渐进面在内的离散形式曲面车削刀触点生成方法。实验结果表明该方法能够实现渐进面加工，工件面型误差为25 μm，表面粗糙度Ra为0.283 μm。