基于凸轮设计理论的多关节机械手轨迹规划
朱建强,田 方
(沈阳工业大学 机械工程学院,沈阳 110870)
0 引言
在对机械手进行运动控制时,在一般低速运动情况下,只要保证关节角度不超限即可,这对运动轨迹规划影响很小。但是,当机械手运动速度较快时,关节角加速度和角速度极易超出约束范围,影响控制精度和损坏硬件。因此,在机械手轨迹规划时需要考虑约束条件,SARAVANAN 等[1]使用NURBS曲线规划机器人运动轨迹,通过优化运动时间使得轨迹能够满足多种约束条件。同样,用3次多项式规划策略插关节轨迹[2-3]和基于3次样条曲线的时间最优轨迹规划方法[4-5]只能保证速度、加速度连续,而不能保证脉动连续,也无法处理脉动约束问题。WANG等[6]提出一种基于一种简化运动规划的新方法满足运动约束。还有XU等[7-8]通过优化B样条曲线的参数,获得满足关节约束的运动轨迹。在运动时间是确定的情况下,无法通过优化时间来解决约束问题时。本文对关节运动加速度进行优化,结合对凸轮从动件运动轨迹设计的研究,提出一种改进梯形加速度曲线函数。该方法适用于工作任务为点到点,且起始点和终止点速度、加速度都为零的工业机械手进行轨迹规划。以3R机械手为载体仿真,该方法成功的改善了关节最大加速度过大问题,使机械手运行轨迹平稳,产生协调的机械手运动。
1 凸轮设计理论分析
在凸轮设计的基本规律中要求凸轮函数必须在整个间隔(360°)内通过位移的一阶、二阶导数连续。这和多关节机械手轨迹规划有着相同的要求,在关节空间中进行轨迹规划是将关节变量q利用不同的函数曲线表示时间的函数,同时规划各关节的一阶、二阶导数,有必要时还需要规划它的三阶导数(即冲击)。在凸轮设计中,为保证函数二阶导数曲线平滑且连续,从加速度函数着手,谐波系列函数的优势使之能应用到凸轮设计中。图1显示了一个加速度函数的全周期正弦曲线。它满足了末端幅值为零的约束。正弦波的方程为:
(1)
通过将自变量θ除以间隔β的时段并且使用弧度测量θ和β。θ/β的值在0~1范围内。乘以2π得到一个完整周期的正弦波,无论β的值如何,正弦函数的参数都将在0和2π之间变化。常数C定义正弦波的幅。对加速度积分获得速度。
(2)

图1 正弦加速度函数
这里k1是常数。为了约束在停驻点时速度为0,代入边界条件v=0 在θ=0 。得出k1为:
(3)
在时间间隔β的另一端替换边界值,v=0,θ=β,k1得到同样的结果。再对速度积分得出位移:
(4)
为了约束在停驻点时位移为零,代入边界条件s=0 在θ=0 ,得到k2。凸轮从动件在间隔β内所需上升最大值为h并且对于任何一个凸轮规格而言都是常数,代入边界条件s=h,θ=β,得出C,k2=0。
(5)
代入C,得到加速度函数为:
(6)
代入C和k1,得到速度函数为:
(7)
代入C、k1和k2,得到位移函数为:
(8)
谐波系列函数很好的满足了凸轮设计的要求,但具有较大的加速度以及速度。在具有运动约束的情况下,较小的运动加速度容易超出约束范围,而较大的加速度不利于机器人运动的平稳性和轨迹跟踪精度。理想的轨迹规划方法应当是在满足约束的前提下,尽量采用较小的加速度。通过依次对角加速度约束、角速度约束和角度约束进行分析和处理,结合凸轮设计理念提出新的轨迹函数来实现轨迹规划,下面给出具体步骤。
2 改进梯形加速度函数
选择合适的角加速度曲线类型对处理约束问题至关重要,最能够发挥机器人关节运动性能的角加速度曲线。为了减少因为加速度过大而引起的轨迹误差,关节最大加速度应该减小并保持连续。如果使给定问题的加速函数幅值的峰值最小化,那么最能满足这个约束条件的函数就是如图2所示的方波,称为恒定加速度函数。方波具有给定区间内给定区域内最小峰值的特性。由于它有很强的不连续性,因此,用来作为轨迹加速函数是不可行的。

图2 常数加速度函数图
方波的不连续性可以通过简单地将方波函数“直角”去除,使函数变得连续,并创建如图3所示的梯形加速函数。必须通过增加高于原始方波的峰值来替代去除的区域,以保持恒定时间所需满足位移的要求。该函数峰值幅度的增加很小,并且理论上最大加速度显着小于正弦加速度(摆线位移)函数理论上的峰值。但该梯形函数的一个缺点是它有非常不连续的冲击函数,如图3所示。这样不连续的冲击函数会导致机械手剧烈的震动,影响精度和损害硬件。

图3 梯形加速度函数图

图4 改进梯形加速度函数图
正弦加速度具有相对较平滑的余弦冲击函数曲线,在间隔内只有两个不连续点,并且优于梯形加速度方波。如图4所示,对梯形加速度函数进行改进,称为改进梯形加速度曲线。该函数是正弦加速度和恒定加速度曲线的结合。把全周期正弦波切割成4份,并且组合到方波中,使得从端点处的零到最大和最小峰值的平滑过渡,并且使得曲线连续。用于函数的正弦部分的总段周期(β)的部分可以变化。本文是在β/8,3β/8,5β/87,β/8处切割方波以插入正弦波,如图4所示。
基于以上凸轮设计理论的研究并且满足运动约束条件的情况下,该方法可应用于工业区自动化生产线上的机器人,如搬运机器人、检测机器人、装配机器人、点焊机器人等。这些工作任务是点在关节空间的机械手轨迹规划中,起点和终点的关节角速度和角加速度为零,工作任务要求与凸轮设计的凸轮从动件运动轨迹要求相同,在多关节机械手轨迹规划中,结合正弦加速度函数以及机械手工作任务要求得出改进加速度函数。在机械手关节空间内,凸轮轨迹函数中上升的最大高度变化h即是最大关节角度变化θmax、角度间隔β即是时间间隔T、时间变量即为(t-t0)。
2.1 角加速度函数分析

(9)
2.2 角速度函数分析
当角加速度满足要求之后,考虑角速度的约束。较小的关节角速度,减小了机械系统的动能,特别是对大质量的物体。根据边界约束条件,在初始t0时刻和终止时刻tf,角速度约束为0,根据式(7)、式(9)可得:

(10)
2.3 角度函数分析
当角加速度和角速度都满足要求之后,考虑角度的约束。根据边界约束条件求得的方程,所以与传统5次多项式插值方法一样,满足关节角度的约束。在初始t0时刻关节角度为θ0,终止时刻tf关节角度为θf,根据式(8)、式(10)可得:

(11)
由以上步骤最终得到的加速度是同时满足角加速度约束、角速度约束和角度约束的最小加速度。
3 工作任务
以3R多关节机械手为载体,合理的设置机械手工作任务点A(550,0,-550)和B(800,0,0)并在MATLAB Robotics Toolbox中仿真出A点和B点的末端执行器位置[9],如图5所示,通过逆运动学方程解出对应点关节的角度变量,如表1所示。

图5 机械手工作任务点

表1 关节空间任务点
4 仿真
传统轨迹规划采用5次多项式过渡连续曲线函数[10],其2阶导数也是连续的,可以使运动轨迹、运动速度和加速度都连续平滑。这有利于高速运动,同时减少急速运动所加剧机构的磨损和减少机器人操作臂的共振。同样满足加速度轨迹的连续性且工作任务要求(起始点和终止点的角速度,角加速度为零)与本文所提出的轨迹规划方法进行仿真比较。采用3R多关节机械手为载体,通过仿真对本文所提出的轨迹规划方法进行说明,为了更能说明文中所提轨迹规划方法的效果,同时采用5次多项式规划进行比较,由于篇幅有限,只展示关节2仿真结果,如图6所示。图6显示了关于关节2的角度、角速度和角加速度与时间曲线的关系。表2分别列出了这两种方法的每个关节轨迹的最大加速度比较。可以看出,本文提出的方法的两个关节的最大加速度均小于5阶多项式插值方法的关节轨迹最大加速度。以第2关节为例,如图6所示,该方法产生的最大加速度值为52.9653°/s2,而5次多项式插值方法对应的最大加速度值为62.5587°/s2,约为前者的1.18倍。该方法用改进梯形函数特性不仅满足了任务要求条件,且减小了最大加速度峰值。这两种方法都可以实现相同的工作任务,即初始位置和目标位置之间的点对点轨迹规划,但所提出的方法会产生更小的关节加速度轨迹。因此,本文方提出的轨迹规划方法更加可行和有效。
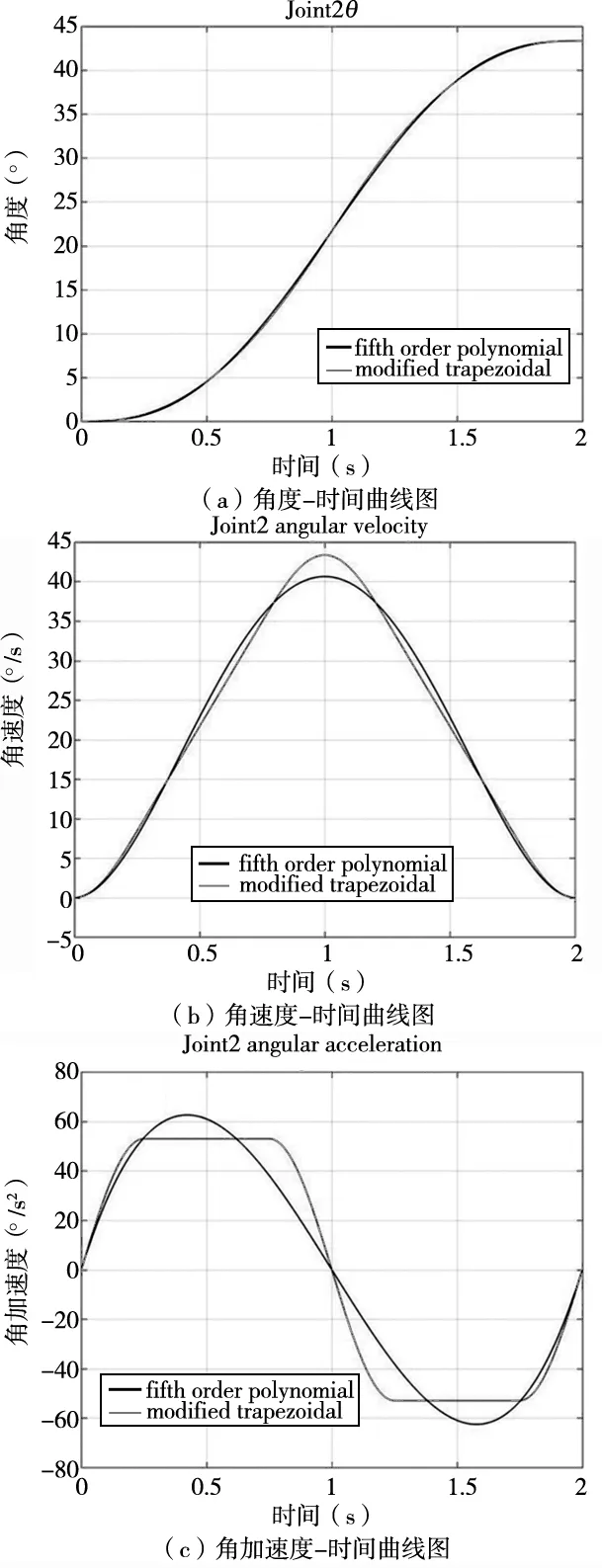
图6 关节2角度,角速度,角加速度图

表2 各关节最大加速度比较图
5 结论
本文采用改进梯形加速度轨迹函数方法,得出以下结论:
(1) 本文提出的轨迹规划方法与传统的5阶多项式插值轨迹规划方法相比,既保证了多关节机械手轨迹运动时角速度和角加速度光滑连续,且减少了关节最大加速度,提高了机械手关节运动轨迹的光滑性和精确度。
(2) 改进梯形加速度函数曲线,保证了起始点和终止点的角速度与角加速度为零,且关节加速度曲线在起始点终止点处连续变化,消除了机械抖动。
(3) 关节空间轨迹规划存在一个共同的缺点,就是不利于处理避障问题,这是有待进一步研究的地方。

