6自由度串联机械臂的逆运动学算法优化与验证

童水光，王 敏，从飞云,童哲铭

(浙江大学 机械工程学院，杭州 310027)

0 引言

目前机械臂已广泛应用于生产制造业，对机械臂的精度和实时性要求也越来越高。而机械臂的逆运动学分析作为机械臂运动学的重要组成环节，直接影响机械臂的位置精度、动力学特性和实时响应性，但目前其求解过程涉及大量矩阵乘积，矩阵求逆等非线性方程组的计算，求解复杂耗时[1-3]。

针对这一问题，国内外学者提出一些改进的方法，付中涛等提出基于符号运算预处理和矩阵特征向量提取的算法[4]，通过矩阵拆分和符号运算消去系数矩阵中的未知变量，采用矩阵特征值的分解和特征向量的选取得到逆运动学的16组解；T Ao等提出结合旋量和代数方法的工业机械臂逆运动学解法[5]，利用工业机械臂最后三个关节依次两两垂直的结构特点进一步简化计算过程；林阳等提出基于多种群遗传算法的机械臂逆运动学算法[6]，采用动态变异率的变异算子，种群替代和个体替代相结合的移民算子来克服全局收敛的盲目性。

现有的逆运动学求解方法大多数都是利用数值法或几何法单独实现[7-9]，需要庞大的计算量，而一些智能算法程序复杂，需要高性能的计算机配置，且存在稳定性不足的问题[10]，本文利用旋转子矩阵正交的特性和位姿分离思想对一般6自由度串联机械臂的逆运动学解法进行改进，利用位置子矩阵用来求解前3个关节变量，旋转子矩阵用来求解后3个关节变量，求解过程简单明了。此外，对一般6自由度串联机械臂存在的奇异点问题和多解问题也进行了详细的说明。最后在RobotStudio仿真和汽车轮毂打磨的实际工况中进行验证，结果表明，该算法有效且缩短了求解时间，满足机械臂工作的实时性要求

1 算法基本思想

1.1 位姿分离思想

从机械臂的结构设计角度出发，6自由度机械臂有3个自由度用于规定位置，另外3个自由度用来规定姿态[1]。利用这一思想，可以从位置和姿态分别联立方程组求解正运动学方程。利用Denavit和Hartenberg提出的描述机械臂各连杆之间运动关系的通用方法(以下简称Denavit-Hatenberg法)建立坐标系[11]，得到机械臂末端与基座的关系为[1]：

(1)

其中，R表示旋转子矩阵，P表示位置子矩阵，根据位姿分离思想，位置子矩阵用来求解前3个关节变量θ1～θ3，旋转子矩阵用来求解后3个关节变量θ4～θ6。

因旋转子矩阵是3阶方阵，相比于传统方法直接用4阶方阵T求解，该算法对矩阵进行了降维，可有效简化运算，缩短运算时间。

1.2 正交矩阵

在传统解法中，求解后3个关节变量θ4～θ6时，需要对3个变换矩阵T1T3T3求逆矩阵，将4、5、6关节进行解耦，运算复杂。

经证明R-1RT=E，即旋转子矩阵为正交矩阵，因此可以利用正交矩阵的性质：矩阵的逆等于矩阵的转置，R-1=RT，避免求逆矩阵的复杂运算，简化运算过程，提高机械臂逆运动学求解的运算速度。

2 算法实现

本文以ABB IRB1600机械臂为例进行运动学建模，并进行运动学分析。

2.1 运动学建模及正运动学分析

ABB IRB1600的平面CAD图如图 1所示。自下至上主要由基座、腰部、大臂、小臂、腕部组成。

图1 ABB-IRB1600机械臂

由Denavit-Hatenberg法建立连杆坐标系进行运动学建模，给每一个关节指定一个参考坐标系，从基座到第1个关节，再从第1个关节到第2个关节直至到最后一个关节的所有变换结合起来就得到了机械臂的总变换矩阵[3]。z轴位于按右手规则旋转的方向，x轴位于相邻z轴的公垂线方向，y轴按照笛卡尔坐标系右手法则可得，建立好的连杆坐标系如图 2所示。

图2 机械臂Denavit-Hatenberg连杆坐标系

ABB IRB1600的Denavit-Hatenberg参数如表1所示。

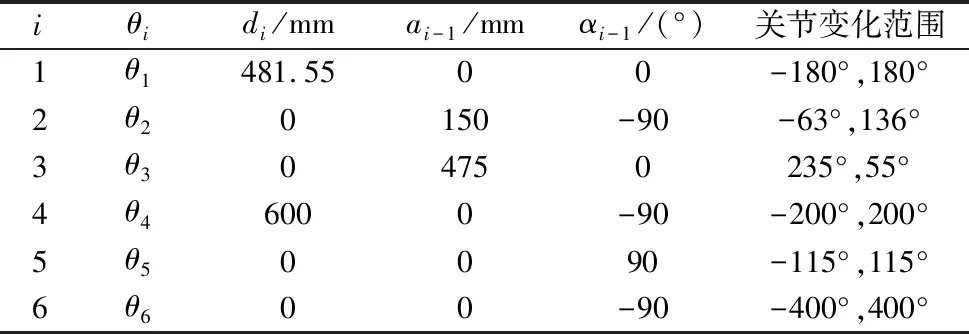
表1 IRB1600连杆参数

表中，ai为沿xi轴，从zi移动到zi+1的距离；αi为绕xi轴，从zi旋转到zi+1的角度；di为沿zi轴，从xi-1移动到xi的距离；θi为绕zi轴，从xi-1旋转到xi的角度。

相邻两连杆之间的变换矩阵通式为[1]：

(2)

根据Denavit-Hatenberg参数，代入式(2)求得各连杆变换矩阵如下：

其中，sθ1=sinθ1，cθ1=cosθ1，以此类推。

各连杆变换矩阵相乘得总变换矩阵为：

(3)

其中，px=c1(a1-d4s23+a2c2)

(4)

py=s1(a1-d4s23+a2c2)

(5)

pz=d1-d4c23-a2s2

(6)

其中，c1=cosθ1，s1=sinθ1，c23=cos(θ2+θ3)，s23=sin(θ2+θ3)。

2.2 逆运动学分析

2.2.1 前三个关节变量的求解

利用位置子矩阵的元素求解。由上式(4)、式(5)联立求得：

θ1=arctan2(py，px)

当c1≠0时，把式(4)、式(5)作如下变换：

T1=-d4s23+a2c2

(7)

T3=-d4c23-a2s2

(8)

其中，

式(7)、式(8)两边分别平方相加，利用三角函数关系式进行化简可得：

-T1c2+T3s2=M

其中，

所以，可求解θ2：

当c1=0时，联立式(5)、式(6)按上述方法求解θ2。

已知θ1，θ2，可联立式(7)、式(8)求解θ3，

所以，θ3=arctan2(s23，c23)-θ2

同样地，当c1=0时，联立式(7)、式(8)按上述方法求解。

2.2.2 后三个关节变量的求解

利用旋转子矩阵求解。相邻两连杆之间的旋转矩阵通式为[1]：

所以4、5、6连杆之间的旋转变换矩阵为：

其中，

(9)

(10)

(11)

(12)

由上文前3个关节角已求得，又因旋转子矩阵正交，所以可得：

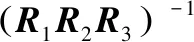
(13)

当s5>0时，θ4=arctan[L(3,3),-L(1,3)]

当s5<0时，θ4=arctan[-L(3,3),L(1,3)]

2.3 奇异点和多解问题的处理

2.3.1 奇异点分析

机械臂的奇异状态指的是某种情况下，机械臂失去了一个自由度，不按所期望的状态运动。一般来说，机械臂有两类奇异点，一类是臂奇异点，一类是腕奇异点[12]。臂奇异点就是腕中心(轴4、5、6的交点)正好位于轴1上方，如图 3所示。腕奇异点就是轴4和轴6处于同一条线上，即轴5角度为0，如图 4所示。

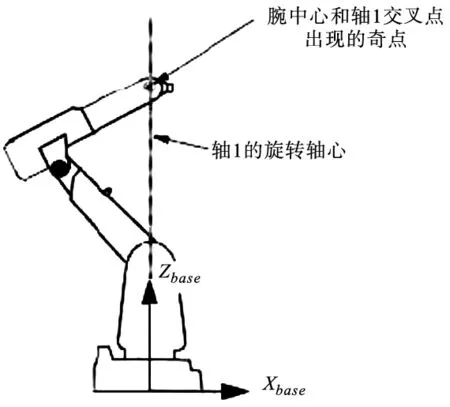
图3 腕中心和轴1汇集时出现臂奇异点

图4 轴5角度为0时出现腕奇异点

在运动学逆解的过程中，应舍去θ5=0的解。另外，在后续的轨迹规划过程中，应选择关节空间轨迹规划的方法而非笛卡尔空间轨迹规划的方法，以避免发生机构的奇异性问题[3]。

2.3.2 多解问题的处理

对于机械臂的逆解过程，由于解的不唯一性，会产生8组解，即机械臂可通过不同组轴角度获得相同的机械臂工具位置和方位。一般来说，解的选取遵循就近原则，利用最接近轴起点位置的轴定位，移动机械臂至设定位置处[13]。

3 算法验证

3.1 Robotstudio仿真

表2 运动学逆解结果

在RobotStudio中，输入给定的期望位姿，得到机械臂各关节角如图 5所示，从上至下分别是θ1～θ6，与算法结果基本一致，验证了该算法的正确性。并且在Windows Sever 2008 R2，128G RAM的服务器平台上运算，该算法实现的时间仅为0.057ms，而用一般封闭解法在相同的试验条件下实现时间为0.11ms，因此该算法可以更好地满足实时性要求。

图5 RobotStudio中机械臂各关节角度值

3.2 实际工况应用

上述仿真是针对单一期望位姿点进行的验证，下面将给出一段连续轨迹曲线进行验证。以基于视觉的汽车轮毂自动化打磨工况为例，如图 6所示，打磨前需提取轮廓轨迹点坐标，然后通过逆运动学算法求取机械臂各关节的角度值，交由机械臂执行，实现打磨动作。

按照本文逆运动学算法求解机械臂各关节的角度值，传输至机械臂控制器IRC5 Compact，控制机械臂执行各关节的目标变换角度，得到机械臂的末端位置，经证明实际加工轨迹与轮毂轮廓吻合，并在MATLAB中绘出连续轨迹曲线如图 8所示，与实际轮毂轮廓曲线段一致，验证了该算法是合理有效的。

图6 基于视觉的汽车轮毂自动化打磨工况 图7 工业相机采集的汽车轮毂图

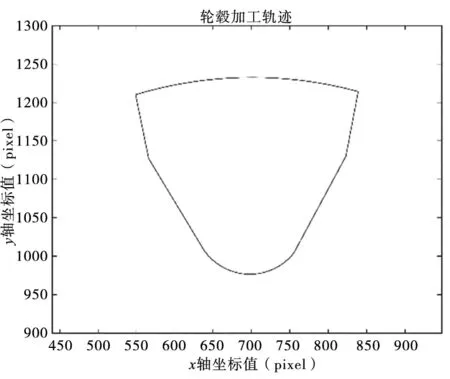
图8 轮毂加工轨迹结果图

4 结论

针对符合pieper准则的一般6自由度串联机械臂[14]，基于封闭解法提出一种改进的逆运动学解法。利用Denavit-Hatenberg法对ABB机械臂运动学建模，确定连杆结构参数，求解机械臂正运动学方程，然后从机械臂结构设计的角度出发，基于位姿分离思想分别利用位置子矩阵和旋转子矩阵求解6个关节角值，并辅以正交矩阵的性质简化运算。针对机械臂的奇异状态和多解问题进行了分析和阐述。最后在RobotStudio中仿真验证了单一期望位姿的求解结果，在MATLAB中验证了汽车轮毂打磨实际工况下连续轨迹点的求解结果，均证明了该算法的有效性和高效性，对提高机械臂的工作效率和实时响应有着重要的意义。