数控机床工作平台机构的动态特性分析*

李灿丽，刘祖国，舒成松，余朝静，卢 泽，张大斌，曹 阳

(贵州大学 a.工程训练中心；b.机械工程学院，贵阳 550025)

0 引言

随着中国制造业的迅猛发展，机床的加工精度日益受到关注，而数控机床工作平台的动态特性是机床加工过程中直接影响加工精度的关键因素[1]。

近年来国内外学者对机床整体做了大量研究，杨玉萍等[2]基于有限元分析方法对立式加工中心床身结构动态特性进行了分析，孟祥志等[3]利用虚拟仿真方法对3-TPS型混联机床进行振动测试及加工仿真分析，马春生等[4]也利用有限元方法对机床床身进行了模态及谐响应分析，得到了机构避免的敏感频率范围，综上学者大多都只是针对机床整体进行动态特性分析。

对此，本论文以数控机床工作平台机构为研究对象，重点分析工作平台的动态特性，利用有限元分析方法对机床工作平台进行模态及谐响应分析，同时以点-面结合的方式分析了振型变化较大的位置，得到了X,Y,Z轴的位移响应曲线，为数控机床工作平台机构的设计提供理论参考依据。

1 工作平台的有限元模型

本文选取的数控机床工作平台结构有些复杂，为了建模及分析的方便，忽略了对结构影响不大的部件，按照实际的工作尺寸并借助Solidworks建立了数控机床工作平台机构的与三维模型，将三维模型文件保存为X-T或IGS格式导入到ANSYS中进行有限元分析[5-6]，简化模型后得到如图1所示的三维模型。

图1 数控机床工作平台机构

在导入模型完成之后，首先，需要对模型的材料进行定义，定义材料的参数为结构钢(密度7850kg/m3，弹性模量200GPa,泊松比0.3)，其次对模型进行网格划分，在划分网格时，采用的是系统均匀自动划分网格[7]，得到网格节点数为148316，单元数为88492。将工作平台看做一个整体，整体由质量M，弹簧K，阻尼C组成的振动系统[8]，该系统在受到外力F作用时会发生一定的变形X，如图2所示，其振动方程为：

MX″+KX′+CX=F

(1)

在分析结构模态时需要忽略结构的外力作用即忽略结构的阻尼，此时得到系统在无阻尼情况下的固有频率为：

(2)

当系统受到外力F=F0sin(f0t)的作用时，系统在共振点处的振幅为：

(3)

图2 平台振动系统

结合图2与式(2)、式(3)我们可以发现，当系统质量不变时，改变结构的静刚度和结构的固有频率，都会使共振点处的振幅发生变化，从而可以得到工作平台的工作性能的好坏。

2 平台动力学分析

模态分析的实质是为了获得平台的固有频率及对应的振型，因此低阶模态对结构影响较大，高阶模态对结构影响较小，因此本文设定模态数为6阶进行研究。在进行模态分析时需要对结构进行约束，由于平台在实际工作中底面固定在机床上，因此设定底面为固定约束。在进行力的约束时，基于有限元静应力分析的基础上，以立铣刀作用于工作平面进行力的计算，计算中立铣刀的进给量为0.1，铣刀的转速为300r/min，最大直径为15mm，齿数为3，铣宽为15mm，最大背吃刀量为8，通过计算得到Fx=1609N，Fy=366N,Fz=556N施加在工作平台上，如图3所示。

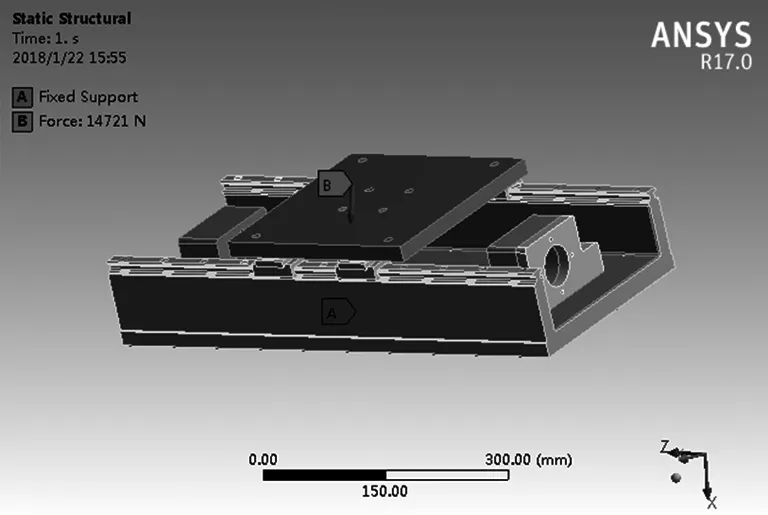
图3 施加约束

静应力分析结果如图4所示。

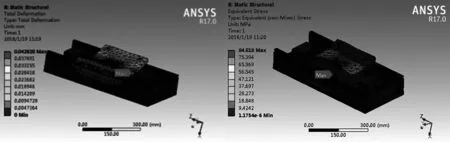
图4 变形与应力云图

通过求解运算得到工作平台的前6阶的模态振型变化，如图5所示。

(a)1阶 (b)2阶

(c)3阶 (d)4阶

(e)5阶 (f)6阶

图5数控机床工作平台前6阶振型云图

表1 数控机床工作平台前6阶固有频率

结合图5中的模态振型云图和表1中的固有频率可以得到：

1阶振型固有频率为854.16Hz，振动变形主要表现在平台表面，呈YZ平面左右弯曲变形，其中在平台与底座连接部位变形最大，最大变形量位11.76mm，振型如图5a所示。

2阶振型固有频率为995.63Hz，振型主要平台的中部，呈ZX平面弯曲变形，在平台前后顶部位置变形最大，最大变形量为14.91mm，振型如图5b所示。

3阶振型固有频率为1185.2Hz，振动变形主要表现在平台底面处，在平台底面部位呈弯曲变形，最大变形量位124.56mm，振型如图5c所示。

4阶振型固有频率为1348.5Hz，振型集中在平台表面及平台底面部位，呈凹凸变形，变形量为75.85mm，振型如图5d所示。

5阶振型的固有频率为2351.7Hz，振动变形主要集中在表面上前后位置，振型最大的位置在平面的角处，平面呈扭曲变形，最大变形量位28.35mm，振型如图5e所示。

6阶振型的固有频率为2407.9Hz，振动变形主要为平面与左右两条支撑梁两部分，呈1阶同向弯曲变形和扭转变形，变形量最大处在左右两条支撑梁上，最大变形量位25.48mm，振型如图5f所示。

通过对数控机床工作平台前6阶振型的比较分析可知，第1,2,3,4阶的固有频率远小于第5,6阶的固有频率，同时表明第1,2,3,4阶的的运动刚度远小于第5,6阶，结合上述的振型频率分析可知，数控机床工作平台表面和平台与底座连接部位的刚度相对于较弱，是平台整体的薄弱环节，为提高结构的稳定性，可以选用刚度较好的材料来替换现有的材料来提高结构的抗振性能。由表1可以知道，结构的最小固有频率为854.16Hz，远大于机床电机的工作频率133.3Hz(转速为8000r/min的电机)，因此，本论文选用的数控机床工作平台的设计有效的避开了结构共振区域，不会因共振而发生破坏。

3 平台结构的谐响应分析

为了获得在不同频率下结构的变形，现采取有限元谐响应的方法对结构进行谐响应分析，因为模态分析只是为了获得结构的固有频率和振型，并不能得到不同频率的变形状况，采用谐响应分析方法对疲劳破坏和共振破坏具有预测作用。本论文利用ANSYS运用模态叠加法对平台机构进行谐响应分析，在求解过程中对机构进行谐响应设置，①载荷的加载沿用静应力分析时的力；②通过模态分析可知6阶的频率为2407.5Hz，对此设置谐响应频率范围为0～5000Hz；为了精确计算结果，将载荷的步数设置100步则对应的节油100个谐响应解，通过设置点-面结合的方式联合分析了平台表面及变形最大点的谐响应变形情况，如图6为平台表面沿X、Y、Z三个方向的位移响应曲线。

(a)X方向

(b)Y方向

(c)Z方向图6 平台表面X、Y、Z方向的位移响应曲线

通过静应力分析知道变形最大点在平台表面中部的前后位置，因此设置图4中变形最大点为谐响应分析的点。得到了变形最大点的X、Y、Z三个方向的位移响应曲线，如图7所示。

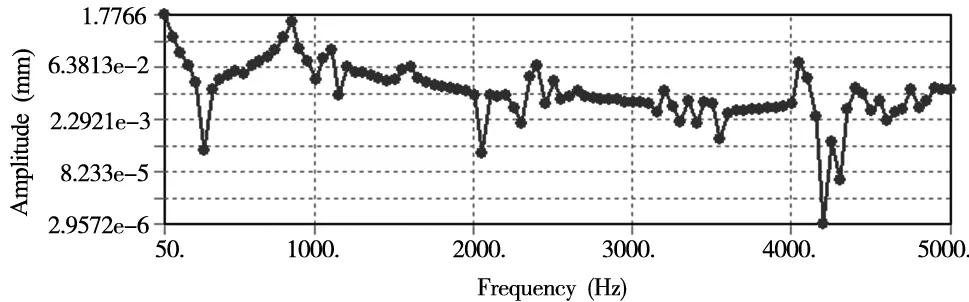
(a)X方向

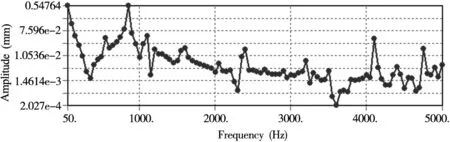
(b)Y方向

(c)Z方向图7 变形最大点X、Y、Z的位移响应曲线

通过观察图6、图7中的位移响应曲线，可以发现：

(1)平台表面在前6阶的固有频率处X、Y、Z方向均为位移最大点，响应也最大。同样在变形最大点处X、Y、Z方向响应也最大，这与模态分析结果保持一致。

(2)平台平面在X轴方向与Y轴方向的位移幅值在模态2阶固有频率周围约1000Hz处达到峰值，变形最大点处沿X轴方向与Y轴方向的位移幅值在模态2阶固有频率周围约950Hz处达到峰值，面与点在发生位移最大时的频率变化不大。平台平面在Z轴方向的位移幅值在第4阶模态固有频率约1400Hz、第6阶模态固有频率约2500Hz处达到峰值，在变形最大点Z轴方向的位移幅值在第2阶模态固有频率约950Hz、第6阶模态固有频率约2500Hz处达到峰值。通过店面结合分析得出了在2阶、4阶、6阶固有频率附近，平台结构在X、Y、Z三个方向发生响应最大，而在其他阶频率处发生的响应相对较小，因此2阶、4阶、6阶对数控机床工作平台的动态特性影响最大。表明数控机床工作平台在工作过程中对995.63Hz、1348.5Hz、2407.9Hz频率最为敏感，因此在设计中和运行中英尽量避免出现上述的频率。

(3)平台表面在X、Y方向和变形最大点在X、Y方向的谐响应位移曲线走势基本一致，表明在这两个方向上平台的移动刚度极度相似，导致这一现象的原因主要是数控机床工作平台的结构是呈对称分布的，因此在分析该平台中，重点考虑Z轴方向的位移变化量。

(4)由于在谐响应中重点分析的是最大点处的位移响应变化，因此从图7中的位移响应曲线可以看出，如果数控机床工作平台不发生共振破坏，在工作时平台在X、Y方向的位移响应一般为0.1mm级，而Z方向的响应较小可以忽略。

4 结论

(1)通过对数控机床工作平台简化模型，再利用ANSYS进行模态分析获得了结构的前六阶的固有频率及振型，从振型云图得到了易发生共振的面及点，同时固有频率值得范围均远大于结构工作频率，验证了结构设计的合理性。

(2)结合模态分析结果对数控机床工作平台进行了谐响应分析，得到了平台在载荷作用下不同频率处的位移变化特性曲线，找到了在2阶(995.63Hz)、4阶(1348.5Hz)、6阶(2407.9Hz)对数控机床工作平台的动态特性影响最大，为合理优化设计工作平台提供重要参考，有易于避开共振的破坏，提高工作精度。