基于Bathe隐式算法的结构动力学显式算法

孟凡涛， 赵建锋

(1. 青岛理工大学 土木工程学院，山东 青岛 266033； 2. 山东华科规划建筑设计有限公司，山东 聊城 252000)

在结构动力计算中，数值积分方法被广泛应用，其中较经典的方法是Newmark-β法[1]、 Wilson-θ法[2]以及Bathe隐式方法[3]等，这些方法精度都很高且均具备较好的稳定性。但是由于隐式方法求解大型方程组，尤其对于非线性问题，需反复迭代计算量较大，因此在实际应用中耗时较多，有其局限性。

Zhai[4]在Newmark-β方法基础上提出了新型快速显式积分法，该方法在求解大型非线性动力学问题时，仅要求质量矩阵M为对角阵，不限制阻尼矩阵和刚度矩阵的形式，不需要求解高阶线性代数方程组，因而提高了数值计算的速度，其截断误差与Newmark-β法同阶，该方法具有较好的稳定条件，且当参数ψ和φ相等且均取为1/2的情况下具有无振幅衰减及周期延长率变化小的优点。但是以上提到的算法没有考虑与结构动力特性协同的问题[5]，所以上述方法不具备结构动力计算的自适应性。

Chang等[6-9]提出了考虑结构动力特性协同的无条件稳定的显式数值积分方法(简称Chang方法)，但其算法是在平均加速度方法的基础上经过一次内嵌的牛顿迭代来实现位移显式表达，其方法仅仅是位移考虑了与结构动力特性的自适应性。Chang方法随着其位移表达式中的积分参数不断改进，其算法性能也再不断提升，并发展了一种带耗散特性的算法，但其速度项仍不具有考虑结构动力特性协同的自适应性。随着快速拟动力试验技术及实时子结构试验技术的发展，显式数值积分算法更加突显出其优势。Chen等[10-11]利用控制理论[12]提出了一种考虑结构动力特性协同的无条件稳定的显式积分算法。其后Gui等[13-14]在其基础上引入了控制周期延长率的参数，使得该种算法更加完善。Rezaiee-Pajand等[15]利用控制理论在翟婉明提出的算法的基础上发展了USE(Unconditional Stability Explicit )算法，该种算法可以考虑结构的动力特性协同问题，但其不能控制周期延长率的变化。遗憾的是Chang方法、Chen等的CRM(Chen and Ricles Method)以及USE算法均存在异常的振幅增长现象，需引入外荷载项的差分来补救和消除这种现象[16]。

Namadchi等[17]利用Bathe隐式算法的放大矩阵提出了半显式的SEUSBCM算法。本文则结合控制理论在Bathe隐式算法的基础上利用CRM的位移和速度表达式发展了一种带耗散特性的双显式无条件稳定的新算法。因此，可称本文方法为(Explicit Unconditionally Stable Time Integration Based on the Composite Scheme Method，EUSBCM)。EUSBCM具有与Bathe隐式复合积分算法相同的数值特性，但EUSBCM是一种单步积分算法，不同与Bathe隐式方法积分步内具有子积分步的复合积分。本文对EUSBCM的稳定性和精度包括数值耗散和色散均进行了分析，以及与其它积分算法的对比工作，并给出了应用于MDOF(Multi-Degree-of-Freedom System)时两个积分参数α2，α1的推导过程及表达式。最后线性和非线性数值算例验证了本文所给出的方法的有效性和正确性。EUSBCM具有较强的耗散特性，根据实时子结构试验的具体试验研究[18-19]并结合笔者以前对实时子结构试验算法的研究[20-21]，本文算法在实时子结构试验中应用具有更强的优势。

1 本文显式算法的提出

单自由度弹性系统的动力方程如式(1)所示，本文的数值积分算法位移、速度表达式分别如式(2)、式(3)所示。对于式(2)和式(3)中的参数α2，α1，本文将利用Bathe隐式算法的放大矩阵进行求解。

mai+1+cvi+1+kdi+1=fi+1

(1)

di+1=di+Δtvi+α2Δt2ai

(2)

vi+1=vi+α1Δtai

(3)

由式(1)～式(3)按单自由度体系进行离散系统的z变换，得到的传递函数如式(4)所示。对于Bathe隐式算法的放大矩阵为式(5)所示。放大矩阵所对应的特征值的行列式如式(6)所示。将式(6)化简后可得到式(7)。联立式(4)中的分母项中的一次项系数和常数项与式(7)中的A1和A2可以得到方程组如式(11)所示。利用Matlab可求得参数α1，α2如式(12)～式(13)所示。

(4)

(5)

|[A]n+1-λ[I]|=0

(6)

λ3-A1λ2+A2λ-A3=0

(7)

(8)

(9)

A3=0

(10)

(11)

(12)

(13)

2 本文显式算法的特性分析

2.1 线性与非线性稳定性分析

由于EUSBCM的放大矩阵与Bathe隐式方法的相同，因此EUSBCM会有与Bathe隐式方法相同的部分数值特性，由于放大矩阵相同，因此EUSBCM对线弹性系统是无条件稳定的，但EUSBCM与Bathe隐式方法最大的不同在于EUSBCM不需要在每个时间步内再进行子分步的计算；为方便分析问题，定于第n+1时步的刚度kn+1与结构初始时刻的刚度k0具有δn+1=kn+1/k0的关系，当δn+1>1时，即为刚度硬化。对于刚度硬化系统，Bathe隐式方法仍是无条件稳定的算法，但EUSBCM是具有条件稳定性的。为了便于说明EUSBCM的稳定性，将Bathe隐式算法、SEUSBCM，EUSBCM，YU implicit M[22]、MKRM[23]进行了比较，如图1所示，EUSBCM具有与Bathe隐式算法、SEUSBCM方法相同的谱半径。对于非线性系统中的稳定性，按照不同的刚度变化进行比较，如图2所示，对于刚度软化系统，EUSBCM是无条件稳定的算法，对于刚度硬化系统，EUSBCM是条件稳定的算法。离散控制理论采用闭环系统分析非线性问题的稳定性，直接积分法闭环系统的结构图，如图3所示。

图1 不同算法的稳定性比较Fig.1 Comparison of spectral curves for various methods

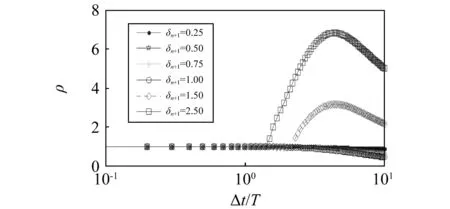
图2 非线性系统的谱半径比较Fig.2 Variation of spectral in nonlinear systems

图3 刚度变化时闭环系统图示Fig.3 Closed-loop block diagram for system with nonlinear stiffness

将式(1)按照单自由度增量形式表述为

mΔai+cΔvi=Δfi-Δri=ΔLi

式中：Δri=ktΔdi根据离散控制理论，闭环系统的传递函数可写为

(14)

其中，

式(14)中分母为零对应的特征方程为式(15)。

(15)

对于非线性系统，将ξ=0.02，ωn=2π rad/s，Δt=0.5 s，m=1代入式(15)，利用Matlab绘制其根轨迹如图4所示。两条根轨迹中有一个分支在z=-1处穿出单位圆并沿着负实轴方向发展，而另一个分支则没有跨越单位圆，将z=-1代入式(15)得到稳定界限如式(16)所示。根据式(16)可以得出随刚度比δn+1i增大，不同阻尼比时的稳定界限如图5所示，可直观的得出当δn+1i≤1，算法是无条件稳定的，当δn+1>1时，算法存在稳定上限，因此算法变成了有条件稳定。

(16)

图4 非线性系统的根轨迹Fig.4 Root locus of nonlinear system

图5 随刚度比变化不同阻尼比时的稳定界限Fig.5 Variation of upper stability limit versus δn+1i for different viscous damping ratios

2.2 精度分析

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

2.3 超调性分析

对于初始条件不为零的单自由度系统(Single-Degree-of-Freedom System,SDOF)，可能会由于时间步长较大而在计算初始时间阶段出现系统的响应被放大的现象，这种现象称为超调。对于一种直接积分算法的超调特性，一般分析一个不考虑阻尼的自由振动系统在无外荷载、初始位移和初始速度不为零的条件下，位移和速度在第一个时间步长内随Ω的变化趋势。本文算法在第一个时间步长内的位移和速度的表达式如式(25)所示。当Ω→∞时由式(12)、式(13)及式(25)可以得到本文算法位移和速度均无超调特性。

(25)

图6 不同算法的PEFig.6 Comparison of relative period error for various methods

图7 不同算法的算法阻尼比Fig.7 Comparison of algorithmic damping ratio for various methods

图8 非线性系统下的PEFig.8 Variation of relative period error in nonlinear systems

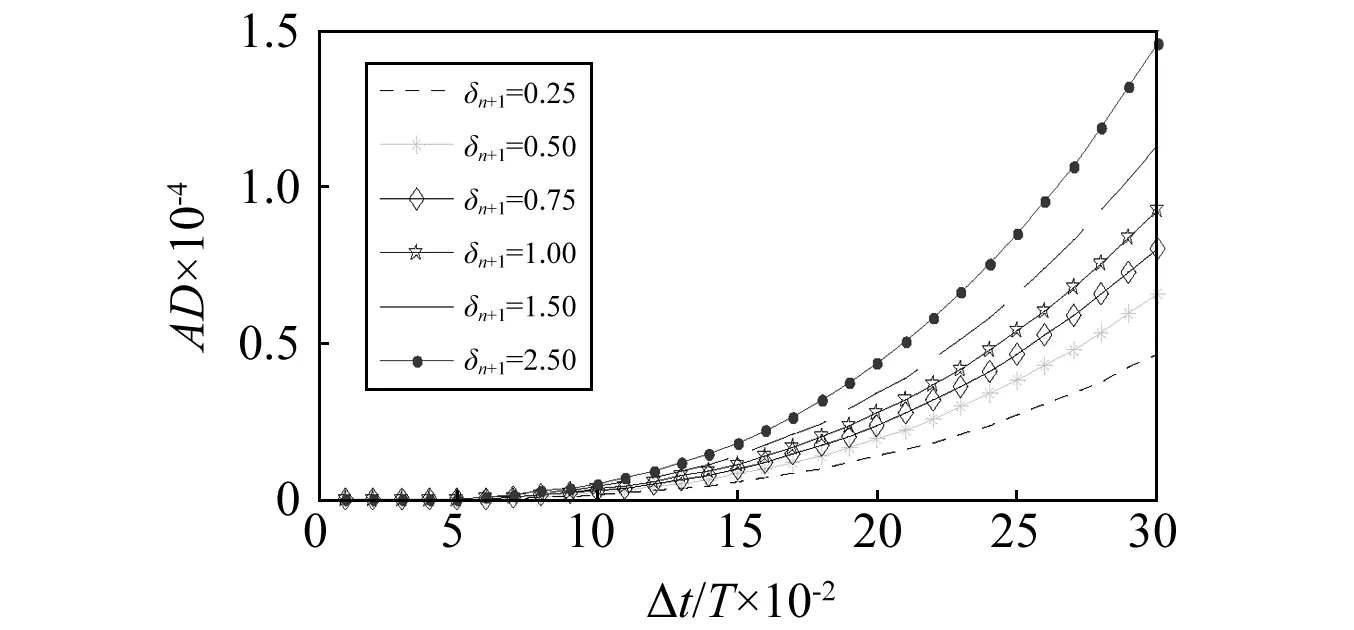
图9 非线性系统下的算法阻尼比Fig.9 Variation of algorithmic damping ratio in nonlinear systems

3 应用于MDOF时[α2]和[α1]的确定

为了得到多自由度系统计算时的[α2]和[α1]，采用模态分解技术将多自由度系统分解为多个单自由度系统，则在模态空间令由式(26)和式(27)成立。式(26)中分子为式(27)所示，分母为式(28)所示。式(29)中分子为式(30)所示，分母为式(31)所示。在模态坐标系中自由振动方程可写为式(32)。将式(32)化简可以得到式(33)。根据式(33)中的参数代入式(26)可以得到式(34)和式(35)成立。化简式(34)和式(35)可以得到式(36)和式(37)，进一步化简可以得到式(38)和式(39)成立，经进一步整理最终得到式(40)和式(41)。将EUSBCM的位移表达式写为模态坐标的形式为式(42)，将模态坐标形式转化为普通形式的位移表达式为式(43),式(43)的参数可得到式(44)成立，由式(44)可以得到式(45)进一步可以得到式(46)，将式(36)和式(37)代入式(46)得到式(47)。同理，将EUSBCM的速度表达式写为模态坐标的形式为式(48)，将模态坐标形式转化为普通形式的速度表达式为式(49)，式(49)的参数可得到式(50)成立，由式(50)可以得到式(51)，进一步可以得到式(52)，将式(40)和式(41)代入式(52)得到式(53)。

由以上推导过程可以得出，在确定多自由度体系的积分参数[α2]和[α1]时，不需处理特征值的计算问题，只要已知结构的初始刚度矩阵，质量矩阵和确定的阻尼比，则可直接利用式(47)和式(53)的结果，该两个参数仅需计算前确定一次即可，即使非线性计算也无需每个时间步内每次都要重新确定该两个参数，即该两个参数仅与结构的弹性初始状态的动力特性和所选定的时间积分步长相关。

(26)

(27)

(28)

(29)

(30)

(31)

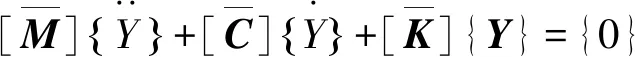
(32)

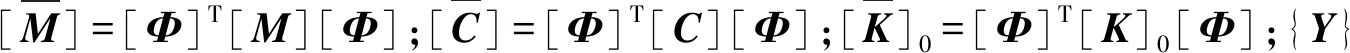
(33)

36Δt([Φ]-1[M]-1[C][Φ])+144[I]

(34)

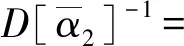
Δt2[Φ]-1[M]-1[K]0[Φ])×

(16[I]+8Δt[Φ]-1[M]-1[C][Φ]+

Δt2[Φ]-1[M]-1[K]0[Φ])

(35)

36Δt([M]-1[C])+144[I]

(36)

(16[I]+8Δt[M]-1[C]+Δt2[M]-1[K]0)(37)

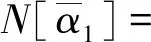
24Δt([Φ]-1[M]-1[C][Φ])+144[I]

(38)

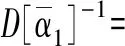
(16[I]+8Δt[Φ]-1[M]-1[C][Φ]+Δt2[Φ]-1[M]-1[K]0[Φ])

(39)

24Δt([M]-1[C])+144[I]

(40)

(16[I]+8Δt[M]-1[C]+Δt2[M]-1[K]0)

(41)

(42)

(43)

(44)

(45)

(46)

[α2]=[(9[I]+6Δt[M]-1[C]+Δt2[M]-1[K]0)×

(16[I]+8Δt[M]-1[C]+Δt2[M]-1[K]0)]-1×

[2Δt2[M]-1[K]0+36Δt[M]-1[C]+144[I]]

(47)

(48)

(49)

(50)

(51)

(52)

[α1]=[(9[I]+6Δt[M]-1[C]+Δt2[M]-1[K]0)×

(16[I]+8Δt[M]-1[C]+Δt2[M]-1[K]0)]-1×

[Δt2[M]-1[K]0+24Δt[M]-1[C]+144[I]]

(53)

4 数值算例

算例1 分析一个单自由度无阻尼线性系统的自由振动，其运动微分方程如式(54)所示。自振频率ω=2π，初始位移为1 m，初始速度为0。位移响应的精确解为x(t)=cos(2πt)，其中时间单位为秒。取积分步长Δt=0.01 s，计算结果与解析解进行比较，对比0～20 s位移时程曲线，由图10能够很直观的得到，所得到的位移与解析解吻合较好。

(54)

图10 Δt=0.01 s时的自由振动位移响应时程曲线Fig.10 Time histories of displacement response with Δt=0.01 s

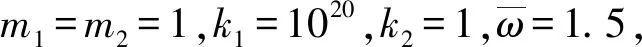
(55)

(56)

图11 质点1的位移响应时程曲线Fig.11 Time histories of displacement response of particle 1

图12 质点2的位移响应时程曲线Fig.12 Time histories of displacement response of particle 2

算例3 一单自由度体系结构质量为39 000 kg 水平刚度为140 000 kN/m，阻尼比为0.05，屈服后与屈服前的刚度比为0.18，恢复力模型为Bouc-Wen模型，该模型的数学表达式如式(57)、式(58)所示。

fs(u,z)=aku+(1-α)kz

(57)

(58)

图13 结构的位移反应Fig.13 Displacement response of the structure

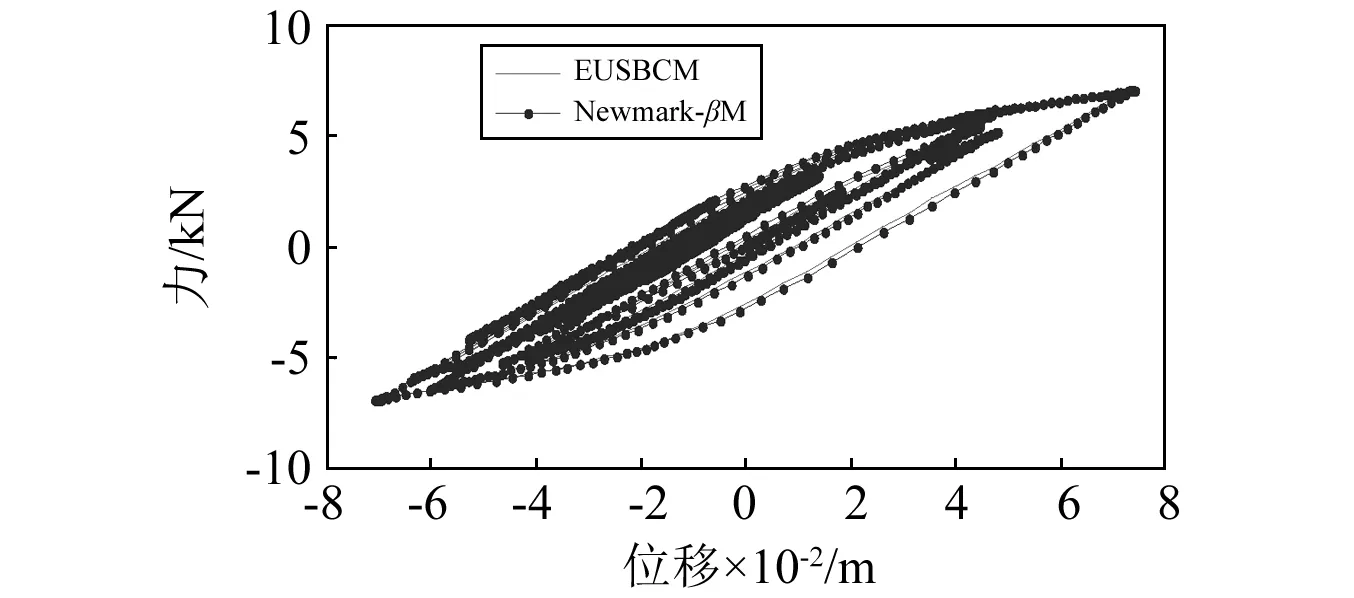
图14 结构的恢复力曲线Fig.14 Restoring force curve of the structure

5 结 论

本文基于Bathe隐式算法，利用CRM的位移和速度表达式发展了一种带耗散特性的显式无条件稳定的新算法EUSBCM。该种算法对刚度软化系统是无条件稳定的，对于刚度硬化系统是条件稳定的。本文基于离散控制理论对于非线性硬化系统的稳定界限给出了理论求解公式。本文算法的位移和速度均是显式的，且仅有两个与结构初始弹性状态及时间积分间隔相关的参数，而SEUSBCM具有四个参数且速度是隐式格式的表达形式，因此笔者提出的EUSBCM的计算效率要高于SEUSBCM。EUSBCM具有较强的高频耗散特性，这是CRM算法所不具有的特性，因此EUSBCM更适合应用于实时子结构试验，且EUSBCM不具有异常的超调现象，无需采用外荷载项的差分进行补救。最后数值算例均表明EUSBCM具有良好的计算稳定性且所计算的结果均与精确解或经典隐式算法的计算结果吻合良好。