钢轨波磨对高速车辆振动特性的影响

刘国云， 曾 京， 张 波

(1. 西南交通大学 牵引动力国家重点实验室，成都 610031； 2. 株洲电力机车有限公司，湖南 株洲 412007)

作为高铁线路的主要病害之一，钢轨波磨是指在一定长度范围内沿钢轨表面纵向所出现的周期性不平顺[1]。根据相关研究，高速铁路钢轨波磨以短波长波磨为主，其波长范围集中在50～130 mm[2]。当列车通过钢轨波磨区段时，不仅会引起轮轨力急剧增大，而且还会导致轨道和机车车辆的剧烈振动，这严重影响到了列车的运行品质，并加大了脱轨的风险[3]。为了控制钢轨波磨的不利影响，确保铁路车辆的安全运行，各国铁路相关部门根据钢轨波磨的成因都采取了相应的预防和减缓措施，同时并制定了相关的钢轨打磨策略[4]。

为了研究钢轨波磨的成因，国内外很多学者已从实验和理论上进行了大量研究。Grassie[5]总结分析了不同钢轨波磨的特点、产生原因以及解决措施，认为目前所有的钢轨波磨都属于固定频率问题。Torstensson等[6]跟踪调查了瑞典地铁车辆以30 km/h的速度通过曲线R120 m上波磨的发展情况以及噪声振动水平。Nielsen[7]通过建立轮对-轨道的相互作用模型，在时域内预测了钢轨波磨的发展。Vila等[8]提出一个研究波磨逐步发展的仿真模型，模型中考虑了轮对的弹性以及轮对旋转的影响。Ling等[9]通过现场试验和仿真计算，分析了钢轨波磨对轨道扣件动态行为的影响，解释了现场地铁线路中扣件疲劳断裂的原因。Zhao等[10]建立了有限元模型，对钢轨波磨处的高速轮轨瞬态滚动进行了求解。温泽峰[11]根据波磨理论计算模型分析了轨道缺陷对钢轨波磨形成和发展的影响。李伟等利用现场试验数据，分析了钢轨波磨对车辆和轨道零部件振动的影响，最后通过数值仿真计算确定了钢轨打磨限值。Wang等研究了波磨波长和深度对高速铁路轮轨动态作用的影响，通过仿真发现，波磨对轮对和钢轨的振动有很大影响，对构架和车体的振动影响很小。

从上述文献可以看出，目前关于钢轨波磨对车辆系统振动影响的研究主要是采取刚体动力学模型来分析，如谷永磊等的研究和文献[12-13]。而随着列车运行速度的提高，轨道不平顺的激励频率已由低频逐渐扩展到中高频段，且车辆与轨道之间的较强动态作用会导致钢轨波磨和车轮多边形等问题出现，从而使高速列车在服役过程中不可避免地出现一些中高频振动响应，而对于只能分析低频段响应的多刚体车辆模型，这时已不再适用。此外，根据相关文献，作为密封轴箱的关键部件，某高速列车的轴箱端盖出现了异常振动，导致连接螺栓出现了松动，这给高速列车的安全运行带来了很大隐患[14]。因此，为了能够实现分析高速车辆中的中高频振动响应，本文在在目前成熟且广泛已知的车辆-轨道耦合模型和车辆系统刚柔耦合模型的基础上，综合考虑了车辆主要部件的弹性振动和轨道弹性振动的影响，对于车辆模型，采用了刚柔耦合动力学理论来模拟车体、构架、轴箱和轮对；在轨道系统中，钢轨是采用梁模型来模拟，轨道板的模拟则采用三维实体有限元模型。利用所完善的分析模型，分析了钢轨波磨对高速车辆系统振动的影响规律，包括不同位置的轴箱端盖以及构架端部的振动加速度，以便更加清楚地认识到钢轨波磨对车辆系统的危害。

1 动力学模型

1.1 车辆系统刚柔耦合动力学模型

在传统的动力学研究中，一般将车辆系统的惯性部件考虑成刚体，大多数情况下这是合理和经济的方式。但当轮轨系统出现伤损时，比如钢轨波磨，往往会激发出车辆系统的弹性变形。因此，为了准确研究钢轨波磨对车辆系统动力学性能的影响，需要考虑部件的弹性变形，建立车辆系统刚柔耦合动力学模型。由于车辆系统的惯性部件如车体、构架和轮对刚度较大，属于小变形，因此可以采用模态叠加法描述结构的弹性变形。本文所建立的车辆系统刚柔耦合动力学模型中主要部件的部分振型及频率，如图1～图3所示。

图1 轮对部分振型Fig.1 Some vibration mode shapes of wheelset

图2 轴箱部分振型Fig.2 Some vibration mode shapes of axlebox

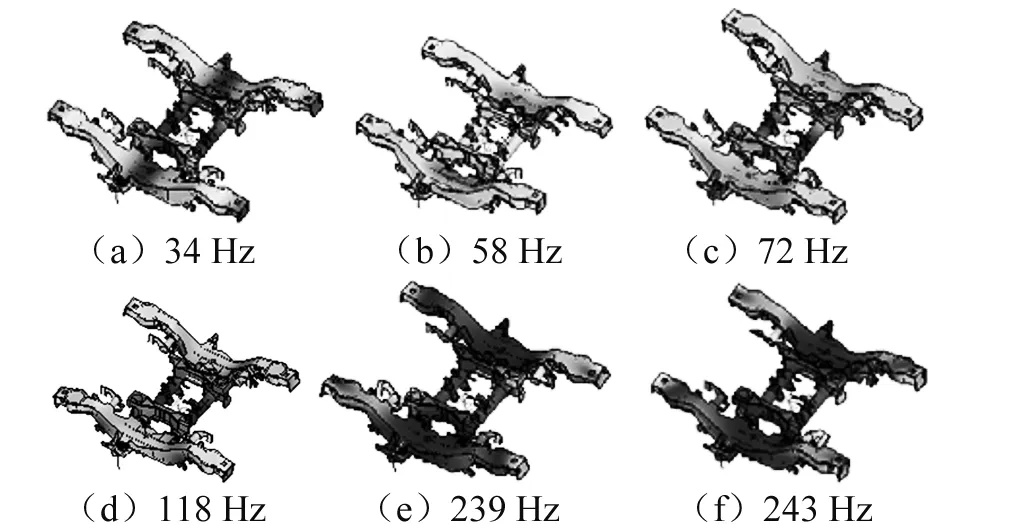
图3 构架部分振型Fig.3 Some vibration mode shapes of bogie frame

1.2 轨道系统动力学模型

本文所考虑的轨道模型为CRTSI型板式无砟轨道模型，包括钢轨、扣件、轨道板以及CA砂浆层组成。其中钢轨的动态行为采用Timoshenko梁模型来模拟，包括垂向、横向和扭转振动；轨道板用实体单元模拟，钢轨扣件和砂浆层用周期性离散的黏弹性单元代替，钢轨的运动方程建立见文献[15]，轨道板的运动方程见文献[16]。

1.3 车辆-轨道耦合模型的实现

由于高速车辆的轮轨系统伤损等非常容易引起车辆的高频振动，在SIMPACK中建立了考虑车体、构架、轴箱和轮对部件为弹性的整车模型。而轨道动力学模型是通过MATLAB建立，其中的钢轨视为连续弹性离散点支承的无限Timoshenko梁，而轨道板用三维实体有限元单元模拟。最后利用SIMPACK与MATLAB的联合仿真接口模块，将整车模型和轨道模型联系起来，实现了车辆-轨道耦合模型的完善，如图4所示[17]。此种迭代方式求解被称为全过程迭代法[18]，在此方法中，首先假定轨道子系统为刚性，求解独立的车辆方程而得到车辆运动及轮轨间作用力时程，然后将轮轨间作用力施加于轨道，求解独立的轨道方程而得到轨道的运动状态，将轨道运动时程与轨道不平顺叠加作为新的车辆系统激励进行下一步迭代。由于采用全过程迭代法，为了保证数值求解的收敛性，因此要求积分步长足够小。

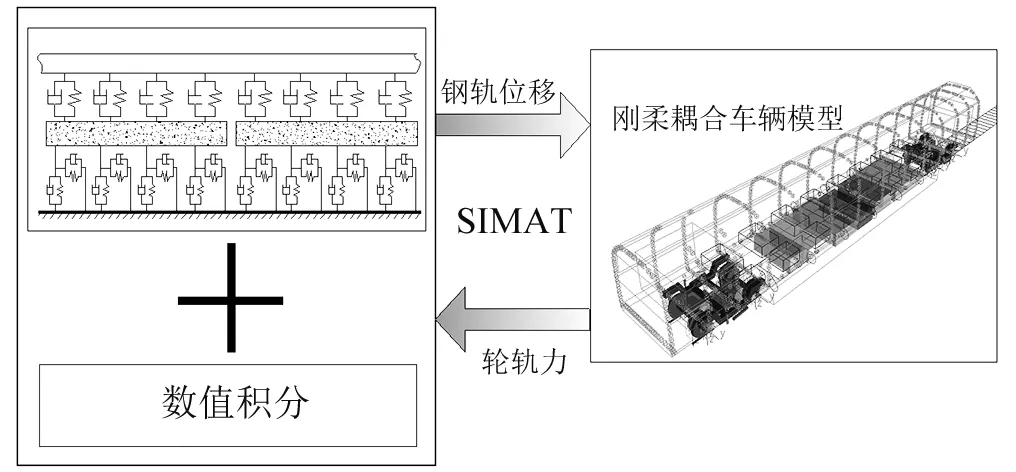
图4 车辆-轨道模型Fig.4 Vehicle-track dynamic model

1.4 轨道子系统数值积分方法

对于轨道子系统，其动力学方程的数值求解采用翟婉明院士提出的新型预测—校正积分法进行求解，具体的求解思路见翟婉明的研究。

1.5 钢轨波磨数学模型

本文在仿真分析钢轨波磨问题时，在不考虑轨道随机不平顺的作用的前提下，采用单一的正弦函数来描述波磨区段的轨面不平顺，即

式中：a为钢轨波磨波深；L为钢轨波磨波长；x为钢轨纵向位置。

2 仿真结果分析

为了分析钢轨波磨对车辆系统振动的影响，假设只有右钢轨出现波磨，并且波磨区段的长度大于转向架轴距，而左钢轨为理想光滑的轨道。为了分析不同车速下车辆系统的振动响应，所考虑的钢轨波磨波长为80 mm，波深为0.1 mm，如图5所示。值得注意的是，在仿真分析波磨问题时，钢轨纵向的不平顺幅值的参考坐标系与铁路坐标系是一致的，即Z轴为垂向向下，为了与现场实际钢轨波磨情况保持一致，论文中已将钢轨纵向的不平顺幅值转化成实际钢轨波磨情况，因此图5中的波谷对应的是钢轨磨耗最严重位置。

图5 理想的钢轨波磨Fig.5 The idealized rail corrugation

2.1 钢轨波磨对轮轨相互作用的影响

以直线轨道为例，且不考虑轨道随机不平顺的作用，仿真分析了速度300 km/h下钢轨波磨对轮轨相互作用的影响。图6给出了波深为0.1 mm，波长为80 mm的钢轨波磨对第2位轮对右轮的轮轨行为的影响，包括轮轨法向力、轮轨纵/横向蠕滑力和车轮磨耗功。从图6(a)可以看出，当初始时刻为钢轨波磨的波谷(钢轨磨耗最严重处)与车轮接触时，随着钢轨波磨幅值逐渐变大，轮轨法向力先增加再逐渐减小，但轮轨法向力出现最大值的时刻要先于车轮滚到钢轨波磨波峰处，也就是轮轨法向力谐波要超前于钢轨80 mm长的波磨谐波。由于钢轨波磨导致了轮轨法向力的波动，因此势必将导致轮轨蠕滑力的波动。从图6(b)和图6(c)可以看出，纵向蠕滑力和横向蠕滑力也均超前于钢轨80 mm长的波磨谐波。从图6(d)可以看出，当车速为300 km/h时，磨耗功最大值出现在波磨波谷(钢轨磨耗最严重位置)的附近，这将导致钢轨磨耗较大侧的磨耗量大于钢轨波磨较小侧，从而进一步加剧钢轨波磨的发展。

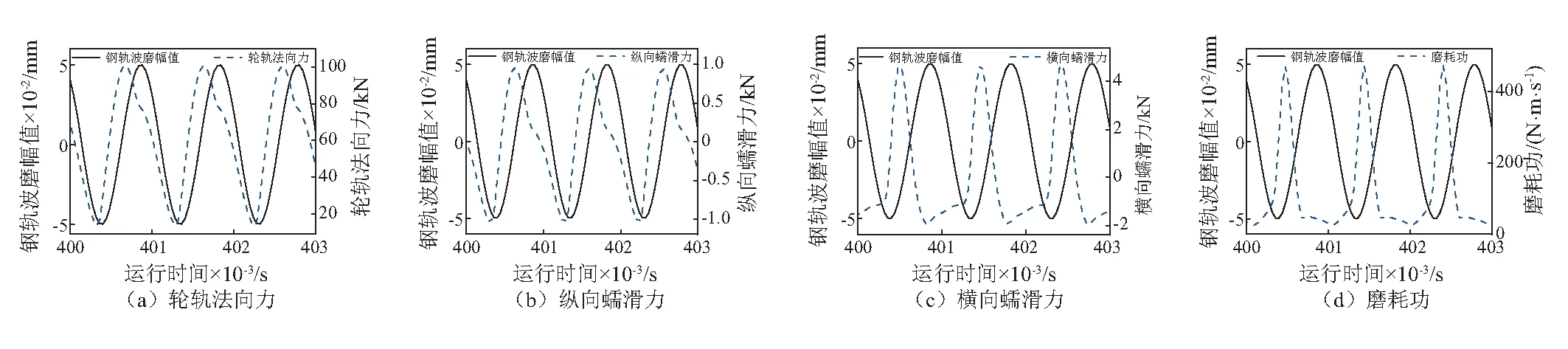
图6 轮轨相互作用的动态响应Fig.6 The dynamic response of wheel/rail force

2.2 钢轨波磨对车辆系统振动响应的影响

由于钢轨波磨导致轮轨作用力的周期性波动，因此势必会对车辆系统的振动产生不可忽视的影响。图7给出了直线轨道上在波长为80 mm的钢轨波磨激励下轴箱端盖的振动响应仿真结果，其中的车辆运行速度为300 km/h，波深为0.1 mm。从图7可以看出，在钢轨波磨的激励下，轴箱端盖的纵向和垂向振动加速度也出现了周期性振动。

图7 轴箱振动加速度动态响应Fig.7 The dynamic response of axlebox acceleration

图8为速度300 km/h下轴箱垂向加速度与轮轨法向力的仿真结果。由于图8中轮轨法向力是指作用在钢轨上的法向力，而作用在车轮上的法向力与它是一对作用力与反作用力，因此，从时域图上看，轴箱端盖垂向振动加速度波动与作用在车轮上的轮轨法向力变化是基本反相的。在仿真模型中，轴箱是通过铰接与轮对发生联系的，即两者的刚体运动之间只存在绕y轴的相互转动。因此这也表明车速为300 km/h时波长为80 mm的钢轨波磨激发出了轮对或者轴箱的弹性变形，导致轴箱端盖出现了比较大的振动。

图8 轴箱垂向加速度与轮轨法向力Fig.8 The dynamic response of axlebox vertical acceleration and wheel/rail normal force

图9给出了速度为300 km/h时波长为80 mm的钢轨波磨对构架端部垂向振动加速度的影响，其中波磨的波深为0.1 mm。从图9可以看出，由于构架端部与轴箱之间采用了一系悬挂装置，因此构架端部垂向加速度与轮轨法向力之间存在有相位差。

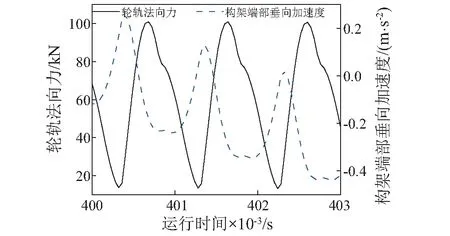
图9 构架端部振动加速度Fig.9 The dynamic response of bogie frame acceleration

由于仿真中假设波磨区段的长度大于转向架的轴距，因此转向架的前后轮对会同时位于钢轨波磨区段内。图10给出了在直线轨道上前后轮对同时位于钢轨波磨区段时前转向架4个车轮位置处的轮轨力仿真结果，其中的钢轨波磨波长为80 mm，波深为0.1 mm，车速为300 km/h。从图10可以看出，由于钢轨波磨出现在右轨，导致转向架的前后轮对右轮的轮轨力均出现了周期性波动，而前后轮对的左轮的轮轨力基本保持不变。由于计算模型为动车转向架，因此同一轮对的左右轮轨垂向力大小不相等。

图10 钢轨波磨对不同车轮轮轨垂向力的影响Fig.10 The influence of rail corrugation on wheel/rail force at different positions

2.3 车速对波磨激励下车辆系统振动的影响

对于固定波长的波磨，车速越高，则其引起轮轨系统振动的频率越高，所产生的轮轨作用力也越大。图11给出了不同速度下在直线轨道上钢轨波磨对轮轨垂向力的影响，其中所考虑的钢轨波磨波长为80 mm，幅值为0.05 mm。从图11可以看出，当车速在40～80 km/h时，轮轨力最大值和最小值均变化相当平缓；当车速在80～200 km/h时，轮轨力最大值急剧增加；速度超过200 km/h后，轮轨力几乎保持不变。

图12给出了不同速度下在直线轨道上钢轨波磨对轴箱端盖纵向和垂向振动加速度的影响。根据图12(a)和图12(b)可以发现，在40～350 km/h速度范围内，轴箱端盖出现了比较严重的弹性振动。以车速210 km/h为例，这时车轮通过波长为80 mm的钢轨波磨所引起的特征频率为729 Hz(f=210/3.6/0.08)，与轴箱的第6阶模态731 Hz比较接近，其振型如图13所示，表现为轴箱端盖处的变形。(图12中的1L指的是第1位轮对左轴箱端盖；1R指的是第1位轮对右轴箱端盖，以此类推)

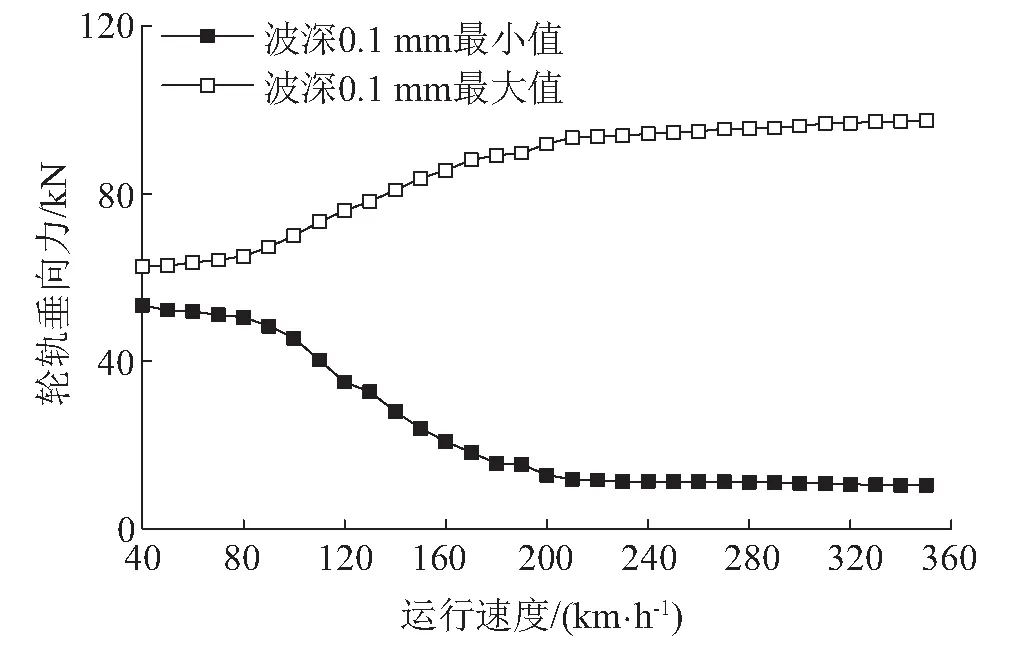
图11 不同速度下钢轨波磨对轮轨力的影响Fig.11 The influence of rail corrugation on wheel/rail force at different speeds

图12 不同速度下钢轨波磨对轴箱端盖振动加速度的影响Fig.12 The influence of rail corrugation on axlebox acceleration at different speeds

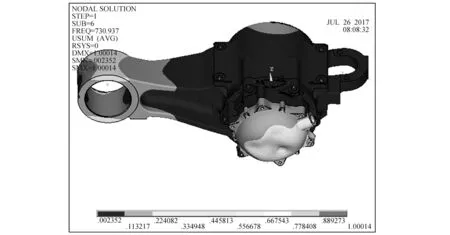
图13 轴箱的第6阶振型Fig.13 The sixth vibration mode shape of axlebox

图14表明，随着速度的增加，波长为80 mm的钢轨波磨所引起的构架端部垂向振动加速度的总体趋势是逐渐减小的。除了在速度130 km/h和200 km/h产生两个峰值点外，构架端部振动加速度还在速度40 km/h和70 km/h下对应有两个峰值点

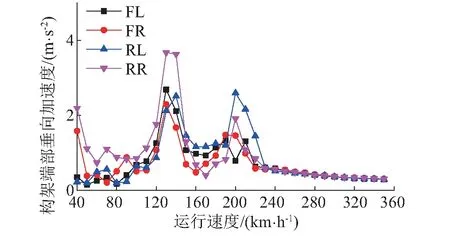
图14 不同速度下钢轨波磨对构架端部振动加速度的影响Fig.14 The influence of rail corrugation on bogie frame acceleration at different speeds

2.4 波磨波长对车辆系统振动的影响

为了研究钢轨波磨波长对车辆系统振动响应的影响规律，仿真中所考虑的钢轨波磨波深为0.1 mm，波长为20～200 mm。图15给出了不同速度下在直线轨道上钢轨波磨波长对轮轨垂向力的影响规律。从图15可以看出，对于所计算的6种速度，轮轨垂向力均随着钢轨波磨波长的增加而逐渐降低；且当钢轨波磨波长一定时，车辆通过速度越高，钢轨波磨所引起的轮轨垂向力的波动值也越大。

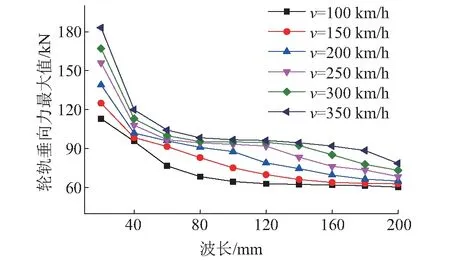
图15 钢轨波磨波长对轮轨垂向力的影响Fig.15 The influence of rail corrugation wavelength on wheel/rail force

图16给出了不同速度等级(100 km/h，200 km/h和300 km/h)下钢轨波磨波长对轴箱端盖振动加速度的影响，其中所考虑的钢轨波磨波深为0.1 mm。从图16可以看出，当速度为100 km/h时，在波长为40 mm和60 mm处对应着轴箱端盖振动加速度的两个峰值点；当速度为200 km/h时，在波长为80 mm和120 mm处对应着轴箱端盖振动加速度的两个峰值点；当速度为300 km/h时，在波长为120 mm和180 mm处对应着轴箱端盖振动加速度的两个峰值点。

2.5 波磨波深对车辆系统振动的影响

图17为在直线轨道上3种不同波深的钢轨波磨几何不平顺激励对前转向架1位轮对轮轨力的影响，其中所考虑的钢轨波磨波长为80 mm，波磨波深分别为0.1 mm，0.2 mm和0.3 mm。从图17可以看出，随着钢轨波磨磨耗的加剧，轮轨垂向力也越大，且开始出现轮轨分离时所对应的速度也越低，这会威胁高速列车的运行安全，因此需要通过定期打磨来严格控制钢轨波磨的幅值以消除钢轨波磨的不利影响。

图17 不同速度下钢轨波磨波深对轮轨垂向力的影响Fig.17 The influence of rail corrugation depth on wheel/rail force at different speeds

图18和图19分别给出了不同速度下钢轨波磨波深对轴箱端盖和构架端部振动加速度的影响。从图18和图19可以看出，随着钢轨波磨波深的增加，轴箱端盖和构架端部的振动加速度也变得越来越大。此外，当速度超过160 km/h后，轴箱加速度很明显并不是随着波深的增加而呈线性增长：以垂向加速度为例，当速度为200 km/h时，波深从0.1 mm变化到0.2 mm时轴箱加速度的增加量约为502 m/s2，而波深从0.2 mm变化到0.3 mm时其增量约为194 m/s2。

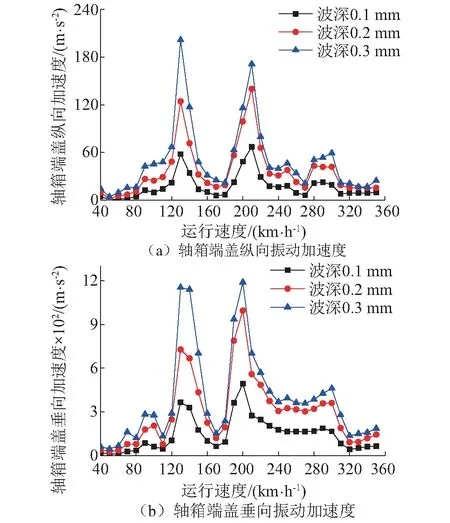
图18 不同速度下钢轨波磨波深对轴箱端盖振动加速度的影响Fig.18 The influence of rail corrugation depthh on axlebox acceleration at different speeds

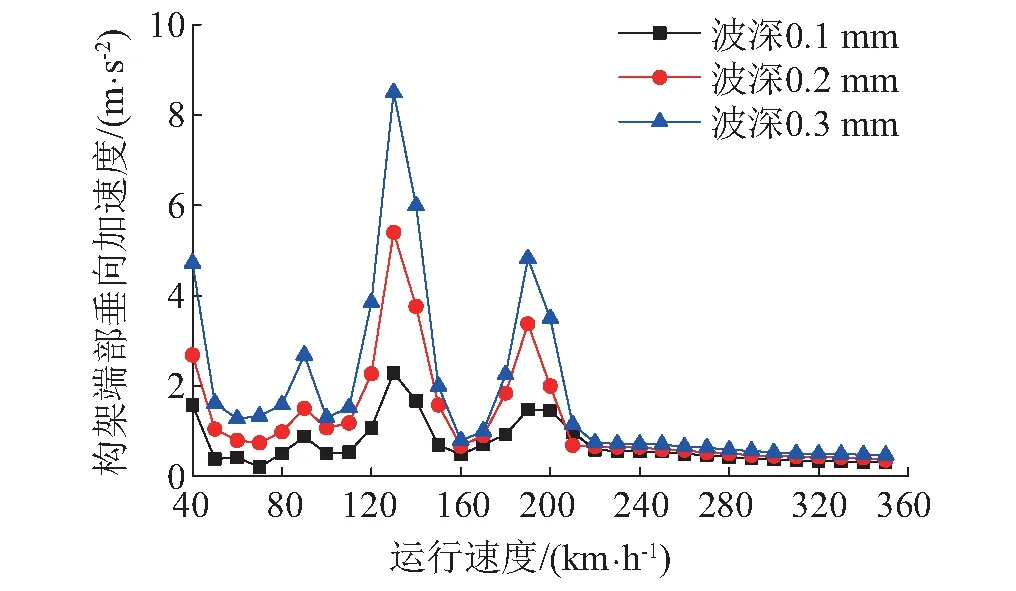
图19 不同速度下钢轨波磨波深对构架端部加速度的影响Fig.19 The influence of rail corrugation depthh on bogie frame acceleration at different speeds

3 结 论

本文基于所完善的分析模型，分析了钢轨波磨对高速车辆系统振动响应的影响规律，包括不同位置的轴箱端盖以及构架端部。通过仿真分析可以得到以下结论：

(1) 钢轨波磨所导致的轮轨法向力、纵/横向蠕滑力和磨耗功与波磨谐波均存在有相位差；当车速较高时，钢轨磨耗较大侧的磨耗功要大于钢轨波磨较小侧，这种磨耗功的分布将进一步加剧钢轨波磨的发展。

(2) 钢轨波磨会导致轴箱端盖和构架端部振动加速度出现周期性波动，其中速度为300 km/h时，轴箱端盖垂向加速度与作用在车轮上的轮轨法向力是基本反相的。

(3) 当车辆以200 km/h的速度通过钢轨波磨(波长80 mm，波深0.1 mm)时，轮轨力的波动变化范围为13～92 kN；同时转向架的4个轴箱端盖和构架端部加速度均呈现出相当大的振动水平：轴箱端盖垂向加速度可达1 190 m/s2，而构架端部垂向加速度可达3.5 m/s2。

(4) 在所计算的速度范围内，随着速度的增加，轮轨力先缓慢变大，然后再急剧增加，最后又保持缓慢增长趋势；且在一定速度下，钢轨波磨会导致轴箱端盖和构架端部出现严重的弹性振动。

(5) 轮轨力随着钢轨波磨波深的增加而变大，随着钢轨波磨波长的增加而减小。