基于VMD 与PSO-PNN 的滚动轴承故障诊断模型

张建财，高军伟

（青岛大学 自动化学院，青岛 266071）

滚动轴承是旋转机械的重要零部件，根据数据显示，大约三分之一的旋转机械故障都是由轴承故障造成的[1]。及时发现并确定故障类型，对故障轴承进行及时的更换或修复从而避免因轴承故障造成的连锁故障进而可以降低设备维护的成本。

长期以来，对于轴承的故障诊断都是通过传感器采集轴承的振动信号，通过各种信号处理方法提取特征向量，然后进行故障类型的识别。经验模态分解EMD（empirical mode decomposition）是一种典型的自适应信号处理的方法，一经提出就被广泛应用到滚动轴承故障特征提取上[2]。然而，EMD 产生的分解高度依赖于极值点搜索、载波包络线插值和终止条件，导致了EMD 存在端点效应、模态混叠等问题[3]。另外，EMD 也存在缺少严格的数学基础和鲁棒性差等问题。变分模态分解VMD 是一种新的自适应信号处理方法。变分模态分解是一种非递归的变分分解模型，运用交替方向乘数法迭代搜寻变分模型的最优解。VMD 方法在采样过程中和抗噪音方面具有很强的鲁棒性，也具有很高的精确度和收敛速度[4]。本文主要采用了变分模态分解方法对振动信号提取故障特征向量。

随着对轴承故障研究的深入，产生了越来越多的故障诊断的方法，例如BP 神经网络、专家系统、支持向量机、概率神经网络[5]。现在大多用的是BP神经网络，但是存在收敛速度慢、容易陷入局部极小值等问题。概率神经网络本身具有训练容易、收敛速度快、分类能力强、不存在陷入局部极小值等优点。然而，难以在概率神经网络中的有限故障模式样本中提炼出能反应整个故障样本空间的平滑因子。本文采用粒子群算法优化概率神经网络中的平滑因子，进而获得平滑因子的最优解。通过Matlab仿真结果表明，与标准的概率神经网络相比提高了诊断的准确性和速度性。

1 VMD 的原理与算法

1.1 VMD 的原理

在VMD 算法中，将本证模态函数IMF（intrinsic mode function）定义为一个调幅—调频信号[6]：

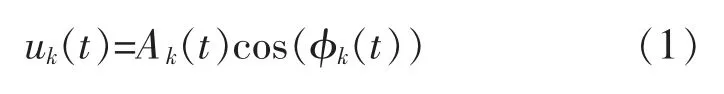
式中：φk（t）为相位且非递减，φk′（t）≥0；Ak（t）为瞬时幅值且Ak（t）≥0。相对于相位φk（t），Ak（t）与瞬时频率ωk（t）＝φk′（t）是缓变的。在间隔范围［t-δ，tδ］（δ=2π/φk（t））中，uk（t）可以看作是一个幅值为Ak（t）频率为ωk（t）的谐波信号。

VMD 是一种时频信号的分解估计方法，变分问题是其整体框架。分解时，根据预设的模态分量个数K 对原始信号进行分解，最终将原始信号f（x）分解成K 个中心频率ωk为的模态函数uk[7]。通过以下步骤得到一定带宽频率的模态函数：①通过希尔伯特变换得到每个模态函数的边际谱；②每个模态函数通过相应的估计中心频率将频谱调制到相应的基频带；③通过计算解析信号梯度的平方L2范数，得到每个模态函数的带宽。构造受约束的变分模型为

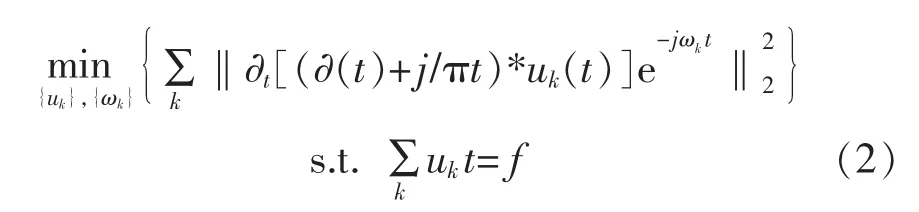
式中：｛uk｝：=｛u1，u2，…，uk｝为模态函数；｛ωk｝：=｛ω1，ω2，…，ωk｝为中心频率为所有模态函数的和。

为了获得方程（2）的约束变分模型的最优解，即每个模态函数，引入惩罚因子α 来构造增广拉格朗日函数：

式中：α 为惩罚参数；λ 为惩罚因子。

将Lagrange 函数从时域转换到频域，并进行相应的极值求解，进一步得到相应的模态分量uk，ωk的表达式：

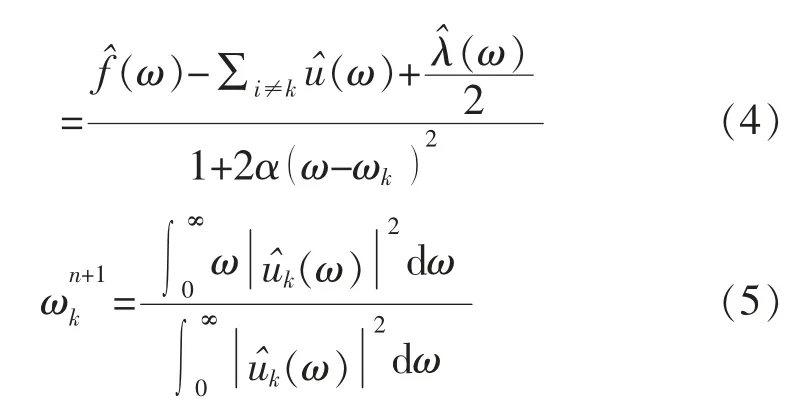
1.2 VMD 的算法

VMD 算法就是将原始信号分解成K 个模态分量，具体算法如下：

（1）初始化 ，，和n；

（3）更新λ，根据式（6）；

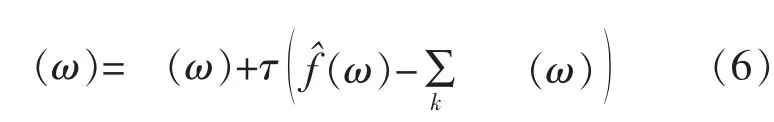
2 PSO-PNN 故障诊断模型

2.1 PNN 神经网络

概率神经网络PNN 是径向基神经网络的一种，在模式分类问题中有比较广泛的应用。PNN 的四层网络拓扑结构如图1 所示。

第一层是输入层，输入层接收来训练样本的故障特征向量，将数据传递给模式层，其神经元的数目和输入向量长度相等。

第二层是模式层，模式层是计算输入故障特征向量与训练集中各个模式的匹配关系，每个模式单元输出为

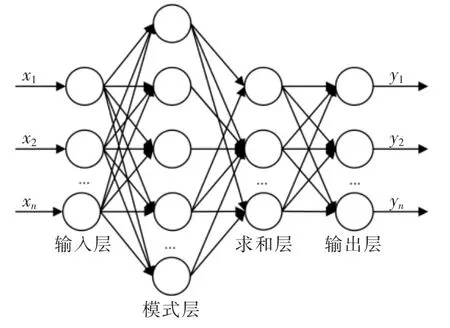
图1 PNN 的四层网络拓扑结构Fig.1 Four-layer network topology of PNN

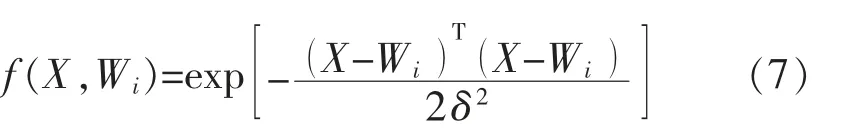
式中：Wi为输入层和模式层之间的连接权值；δ 为平滑因子。

第三层是求和层，求和层是将属于某类的故障模式概率累计，进而得到故障模式的概率密度函数为

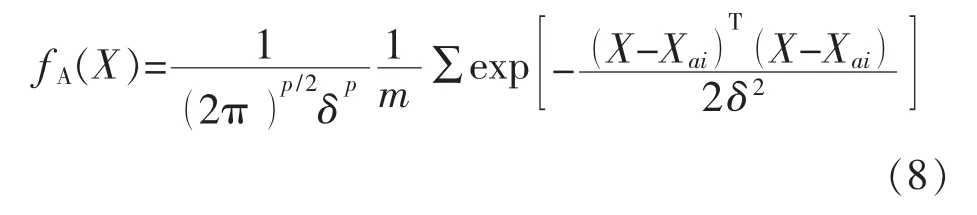
式中：Xai为故障模式a 的第i 个训练向量；m 为故障模式a 的训练样本数目。

第四层是输出层，输出层每一个神经元对应一个故障类型。

2.2 PSO 算法

粒子群算法假设在Y 维的搜索空间中存在n 个粒子组成 的 种 群X=（X1，X2，…，Xn），其中第i 个粒子可以表示为一个Y 维的向量Xi=代表第i 个粒子在Y 维搜索空间中的位置[8]。每个粒子位置Xi对应的适应度值通过目标函数计算得出。将种群中第i 个粒子的速度记为，第i 个粒子搜索到的最优位置记为整个种群搜索到的最优位置记为在种群内不断通过式（9）、式（10）更新自身速度和位置直至求出最优解[9]。

式中：ω 为惯性权重；d=1，2，…，Y；i=1，2，…，n；k 为当前迭代次数；Viy为粒子的速度；c1≥0、c2≥0，称为加速度因子。

基本的PSO 优化算法步骤： ①初始化一个规模为n 的粒子群，设定种群的初始速度和位置；②基于适应度函数计算每个粒子的适应度值； ③将每个粒子的初始位置标记为Pi，全局经历的初始位置标记为Pg；④根据式（9）、式（10）更新粒子的位置和速度；⑤计算新的粒子适应度；⑥将每个粒子新的适应度值和其经历过最优位置Pi的适应度值相比较，若优于，则将其标记为当前最优位置，将每个粒子新的适应度值和全局经历过的最优位置Pg的适应度值相比较，若优于，则将其标记为全局最优位置；⑦判断是否满足条件，若满足条件则结束输出解，若不满足则返回步骤④继续执行。

2.3 PSO 优化PNN 故障诊断模型

概率神经网络本身具有训练容易、 收敛速度快、分类能力强、不存在陷入局部极小值问题并且具有优异的非线性函数逼近能力。平滑因子δ 是概率神经网络中最重要的参数，对网络性能起着至关重要的作用，对提高故障诊断准确性和快速性具有很重要的意义。

然而，在当前的概率神经网络中，难以在有限的故障模式样本中提炼出能反应整个故障样本空间的平滑因子。当前的平滑因子估计是基于经验估计或者是有限的样本聚类方法，此类方法难以充分表达样本空间的概率特性[10]。平滑因子取值难以确定进而影响故障诊断的准确性和速度性，平滑因子δ 的优化对提高故障诊断的准确性和快速性有很重要的意义。粒子群算法对于求解极值最优解具有重要的应用价值，本文主要采用粒子群算法对概率神经网络中平滑因子进行优化并进行故障类型的诊断，流程如图2 所示。

3 实验分析

本文实验数据来自QPZZ-II 故障模拟平台，故障模拟平台如图3 所示，主要由变速驱动电机、轴承、齿轮箱、轴、调速器和信号采集系统组成，轴承型号为N205。

采集滚子故障、内圈故障、外圈故障和正常状态四种情形下的振动信号各20 组，每组包含4096个采样点，滚子故障的原始振动信号的时域波形频谱如图4 所示。

图2 基于PSO 优化PNN 的故障诊断流程Fig.2 Fault diagnosis flow chart based on PSO optimized PNN

图3 QPZZ-II 故障模拟平台Fig.3 QPZZ-II fault simulation platform

图4 原始信号的时域波形和原始信号频谱Fig.4 Time-domain waveform and spectrum of the original signal

3.1 VMD 提取能量特征向量

在分解之前设置模态参数K=4，然后将4 种状态下的原始振动信号进行分解，得到4 个模态分量。计算4 个模态分量的能量Ei，提取能量特征，构建能量特征向量T=［E1，E2，E3，E4］。滚子故障的一组样本数据通过变分模态分解得到的能量特征向量图和能量特征向量柱状图如图5 和图6 所示。表1展示了滚子故障、内圈故障、外圈故障、正常状态下的能量特征向量，由于篇幅所限各个状态的能量特征向量分别展示了4 组。将分解得到故障信号的能量特征向量T 作为故障诊断模型的输入样本。

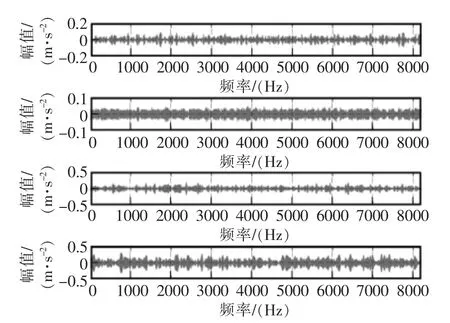
图5 滚子故障能量特征向量Fig.5 Roller fault energy eigenvector

图6 滚子故障能量特征向量柱状图Fig.6 Roller fault energy eigenvector histogram

表1 部分轴承能量特征向量Tab.1 Partial bearing energy eigenvectors

3.2 PSO-PNN 故障诊断

将通过变分模态分解得到的4 种状态的能量特征向量T 分别输入到标准PNN 和PSO-PNN 故障诊断模型中。将每种状态的1～10 组作为训练样本，11～20 组作为测试样本。

在PSO 算法中： 设置加速度因子c1=1.49445；c2=1.49445，将迭代次数设置为为100，初始种群规模设置为30。

3.3 实验结果

本文将PSO-PNN 故障诊断模型与标准PNN 故障诊断模型相比较。图7 为PSO-PNN 模型故障诊断模型测试样本的真实值和预测值，图8 为标准PNN模型故障诊断模型测试样本的真实值和预测值。图7 和图8 中标签1 表示滚子故障、标签2 表示内圈故障、标签3 表示外圈故障、标签4 表示正常状态。

图7 PSO-PNN 模型测试样本的真实值和预测值Fig.7 True and predicted values of PSO-PNN model test samples

图8 PNN 模型测试样本的真实值和预测值Fig.8 True and predicted values of PNN model test samples

通过PSO-PNN 故障诊断模型的滚动轴承故障诊断正确率可以达到95%（38/40），标准PNN 故障诊断模型的滚动轴承故障诊断正确率为90%（36/40），PSO-PNN 与PNN 对4 种故障类型具体的诊断结果正确率如表2 所示。从实验验证角度讲，PSO-PNN的滚动轴承故障诊断正确率要高于标准的PNN 模型，说明了通过粒子群算法优化的概率神经网络在滚动轴承故障诊断中具有较好的效果，提高了故障诊断的正确率。

表2 PSO-PNN 与PNN 对四种故障类型诊断的正确率Tab.2 Correctness of PSO-PNN and PNN in diagnosing four types of faults

4 结语

本文提出了基于变分模态分解与PSO-PNN 的滚动轴承故障诊断模型。通过变分模态分解得到的能量特征向量作为PSO-PNN 故障诊断模型的输入样本。粒子群算法优化概率神经网络模型达到了故障分类识别的目的，通过统计故障诊断准确率，我们可以看出对平滑因子优化后故障诊断的准确率得到了进一步的提高，并且具有较高的学习率，这也为滚动轴承故障诊断提供了一种思路，但是如何进一步提高准确性和速度性还需要进一步深层次研究。