串级模糊控制在多变量单级倒立摆中的应用

王 斌，赵 庆，李巾锭

（天津大学 机械工程学院，天津300072）

倒立摆系统是一种典型的多变量、 非线性、强耦合和快速运动自然不稳定系统，其精确控制的研究具有重要的工程背景和实际意义[1-2]。模糊控制在控制具有复杂性、信息量少和高标准性性能等要求的被控对象时具有一定优势，但模糊控制器的设计等方面还没有得到很好的解决，对于多输入变量被控对象，控制规则数会随输入变量的增多而成指数增加，严重制约着模糊控制器的设计与应用[3-4]。

单级倒立摆有4 个输入变量，若采用常规模糊控制，模糊控制器的控制规则数量非常大，难以实现。文献[5]和文献[6]在研究单级倒立摆解耦的基础上，分别建立了串级模糊控制系统和串级模糊PID控制系统，但二者并没有研究模糊控制器的设计。本文在研究单级倒立摆控制方程解耦的基础上，设计了遗传算法优化串级模糊控制系统，进行了单级倒立摆的串级模糊控制器自动设计。

1 单极倒立摆系统建模

单级倒立摆结构如图1 所示。

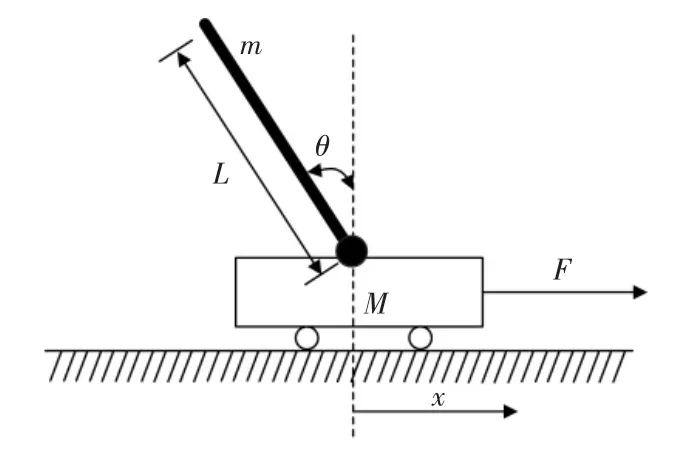
图1 单极倒立摆结构图Fig.1 Unipolar inverted pendulum structure

由式（1）可见，位置变量与角度变量为耦合关系，若直接对其进行模糊控制，模糊控制器有4 个输入变量，若每个输入变量定义5 个模糊子集，则需要625 个控制规则，模糊控制难以运行。本文为了降低模糊控制的难度，对式（1）首先进行解耦，将统一耦合的倒立摆状态方程解耦为2 个独立的状态方程，分别为角度状态方程和位移状态方程：

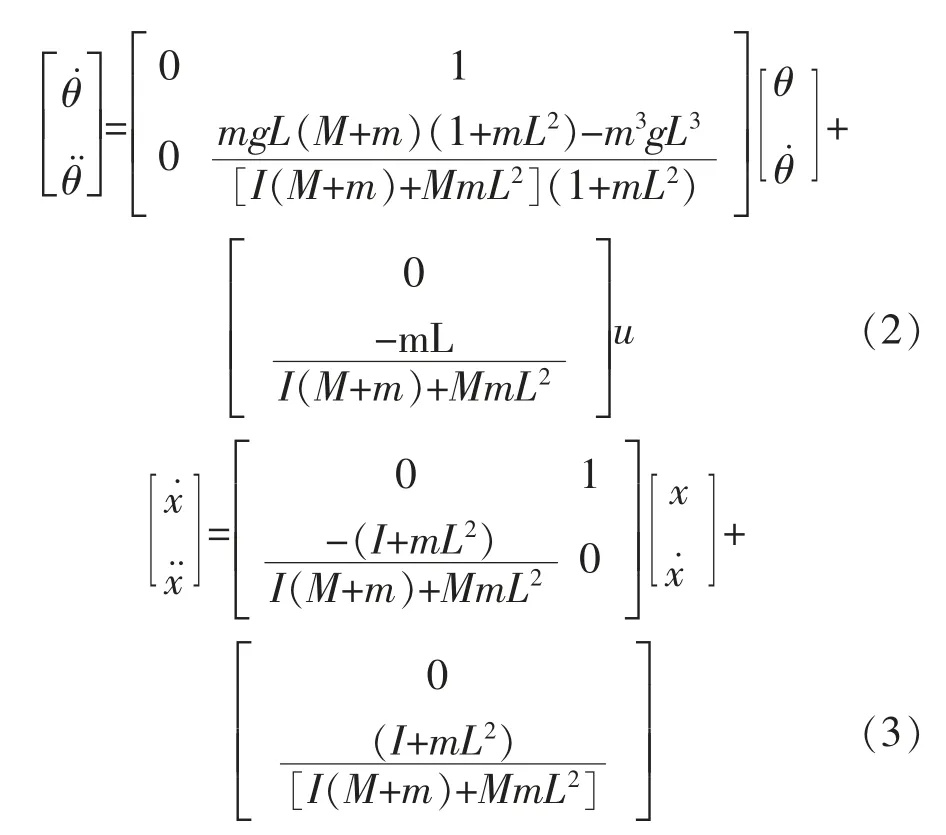
由此，可对2 个状态状态方程直接进行控制。

2 遗传优化模糊控制系统

2.1 串级模糊控制系统

与常用的Mamdani 型模糊推理模型相比较，TS 模糊控制推理模型更便于定量分析和数学运算，本文采用T-S 模糊控制模型，如图2 所示。

图2 双闭环串级模糊控制系统Fig.2 Double closed loop cascade fuzzy control system

由上图所示，串级模糊由2 个模糊控制器组成，其中内环模糊控制器控制单级倒立摆的角度，外环模糊控制器控制单级倒立摆的位移，即运用2个模糊控制器分别控制单级倒立摆的角度和位移。

两个模糊控制器都为二维模糊控制器，设计输入变量都定义5 个模糊子集，每个模糊子集的隶属度都为三角形隶属度：

模糊控制器的规则为配置的反馈极点决定：

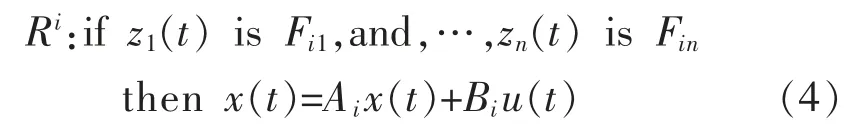
其中u（t）=KIx（t），即此时需要的反馈量，K 为此时的反馈控制增益矩阵，由设置的极点进行极点配置求得。

2.2 模糊控制参数优化

运用并行分布补偿法设计T-S 模糊控制系统就是将模糊控制器分解为多个线性控制器，将T-S 模糊控制器的每条规则作为一个线性控制器处理。并行分布补偿法可分为试凑法和直接法，运用试凑法进行模糊控制器的设计，随机设计每个线性控制器，将它们聚合在一起，即随机设计T-S 模糊控制器的控制规则，若随机设置的T-S 模糊控制系统符合控制要求，则作为设计的T-S 模糊控制系统，否则重新设计。为了实现T-S 模糊控制器的自动设计，采用遗传算法与试凑法相结合的方法设计T-S 模糊控制系统。即将每个试凑法设计的T-S 模糊控制器转化为遗传算法的染色体，并运用遗传算法对其进行参数优化。

采用自适应遗传算法对串级模糊控制器的参数进行优化。遗传算法的输入和输出隶属度都已设计，优化模糊控制器的控制规则。由上文可知，模糊控制器采用极点配置法进行设计，故优化需要的极点。遗传算法流程如图3 所示。其中遗传算法适应度函数、染色体编码及自适应遗传操作需要根据实际问题设置。

图3 遗传算法流程Fig.3 Genetic algorithm flow chart

（1）初始种群生成

染色体编码方式的优劣对遗传算法的运行有重要的影响，本文运用极点配置与并行分配补偿法（PDC）结合的方法产生初始染色体。即将整个T-S模糊控制系统分为多个局部线性控制器，并分别运用极点配置法确定各局部线性控制器的反馈参数。双闭环串级模糊控制器共有50 条控制规则，每条规则代表1 个状态方程，可运用极点配置法将每个状态方程的极点设定为所需要的。每组极点为共轭极点，具有负实部，以这组共轭极点的实部绝对值和虚部的模表示。采用十进制编码，每条染色体有100 个数组成。根据上述编码方法及设定的种群中个体数量，进行初始种群生成。

（2）适应度函数的建立

遗传算法的适应度函数是遗传进化的依据，其确定直接影响着控制模型的优化效果。单级倒立摆的控制需要具有快速性和稳定性，通过多次仿真试探，适应度仅函数以单级倒立摆的小车位移和摆杆角度及为参数标准，确定适应度函数中的各项参数。改进遗传算法的适应度函数如下式：

式中：T 代表采样周期；N 代表采样次数，仿真时间为N*T；j 为采样次数；x1（j）和x3（j）分别为第j 次采样时单级倒立摆输出的位移和角位移。

（3）自适应遗传操作

首先是选择操作中采用最优保存策略，保留上一代中的最优个体，直接进入下一代，代替下一代的最差个体。同时，为了解决遗传算法的早熟问题，提高遗传算法的鲁棒性，本文采用了自适应遗传算法，自适应交叉率和变异率随着个体的适应度在种群平均适应度和最大适应度之间进行调整，并设计了自适应交叉率和变异率：

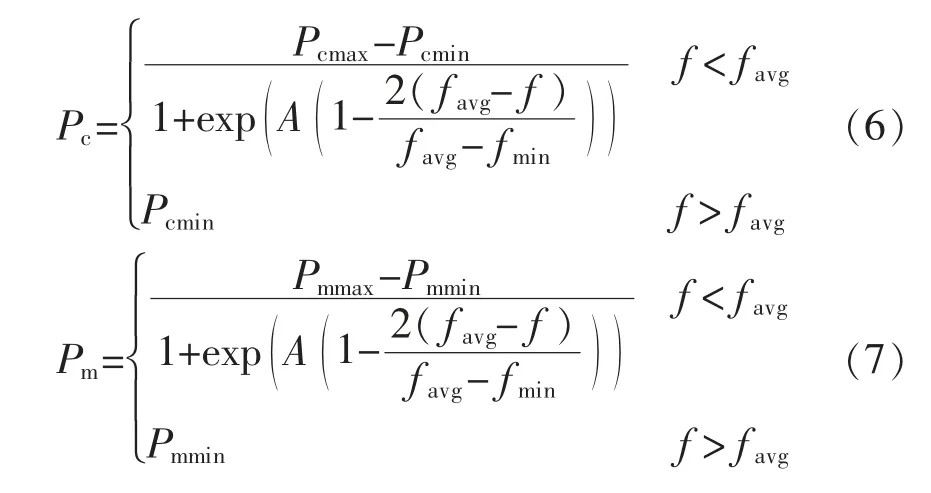
3 实验仿真分析

根据上文设计的模糊控制系统，在Matlab 环境下进行双闭环串级模糊控制器的设计与仿真。取倒立摆的摆杆的初始摆角位移和角度分别为0.2 rad 和0 rad/s，取位移和速度分别为0.1 m 和0.1 m/s。小车的质量和摆杆的质量分别为2 kg 和0.02 kg，摆杆长为0.5 m，小车的摩擦系统为0.1 N/m/s。将上述参数代入控制系统中，运用设计方法对其进行优化，设定遗传算法的初始种群有100 个个体，进化终止代数为100 代，遗传算法的优化过程如图4 所示。

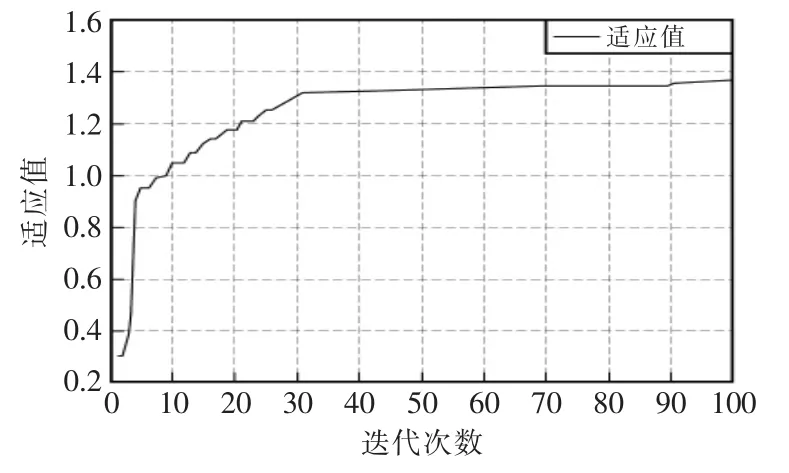
图4 遗传算法优化过程Fig.4 Genetic algorithm optimization process diagram

由上图可知，改进遗传优化过程在前30 代收敛很快，过了30 代，基本趋近稳定，说明改进遗传算法有良好的优化效果。

将优化的控制器参数及单级倒立摆参数代入双闭环模糊控制模型中，对其进行仿真。同时运用同一遗传算法优化双闭环反馈控制系统，将其优化控制结果与串级模糊控制结果相比较，倒立摆的位移控制和角度控制结果图如图5 和图6 所示。

由图5 和图6 中的双闭环串级模糊控制系统和常规双闭环控制系统的控制结果对比可知，相比于常规双闭环控制器，双闭环串级模糊控制系统减小了系统的超高量，缩小了系统的输出振荡，缩短了稳定时间，具有更好的动态性能。

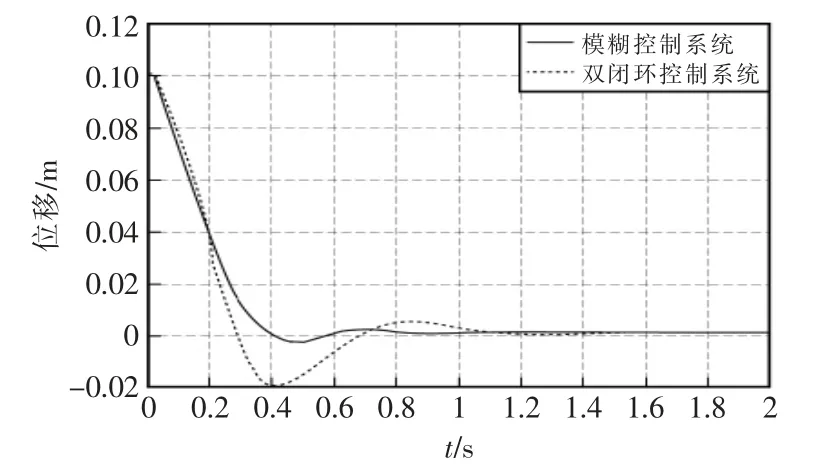
图5 小车位移控制对比图Fig.5 Cart displacement control comparison diagram

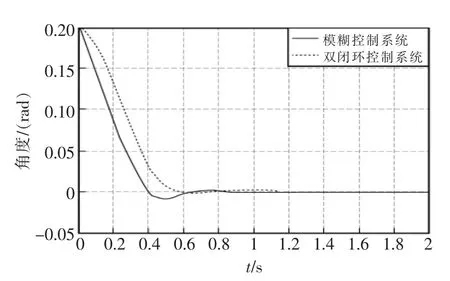
图6 摆杆角位移控制对比图Fig.6 Pendulum angle displacement control comparison diagram

4 结语

单级倒立摆系统的精确控制具有重要的工程背景和实际意义，对其变量解耦以降低控制模型的复杂度和难度是一个重要的研究方向。本文以单级倒立摆控制模型的变量解耦为基础，成为实现了单级倒立摆的双闭环串级模糊控制，将有利于模糊控制在多变量控制模型中应用发展。