D2D 中基于鸟群算法的资源分配和模式选择方案

李永吉，杨永立，王立栋，黄 哲，郭启航

（武汉科技大学 信息科学与工程学院，武汉430081）

设备到设备D2D 通信是5G 中的终端直通技术[1]。短距离的通信用户不经过基站的转发而直接进行信息交互的通信模式是D2D 通信。该方式有效地降低了基站负载、通信时延和路径损耗；由于是短距离直接通信，通信相对安全；通信时消耗功率较低，进而增加了电池寿命[2]；相对于其它不依靠基础网络设施的直通技术而言，D2D 更加灵活，既可以在基站控制下进行连接及资源分配，也可以在无网络基础设施的时候进行信息交互[3]；D2D用户复用蜂窝用户的频谱资源，有效提高了频谱利用率。但是，由于共用频谱自然会造成各用户之间的干扰，现有的很多研究都是围绕解决这些问题展开的。

1 国内外研究现状

文献[4]提出一种基于整体干扰最小的资源分配策略，在D2D 链路质量进行排序时损耗较大；文献[5]在此基础上将问题转化为对资源复用因子进行0-1 的最优指派问题，一定程度上降低了算法复杂度；文献[6]使用频率复用的方法减少小区间的干扰，使用划定干扰限制区域的方法减少小区内的干扰。频率复用的方法虽然可以减少干扰，但是会造成极大的频谱资源浪费，在频谱资源稀缺的现实情况下，显然此种方法实际的使用价值不高。

文献[7]提出了资源分配和资源复用的联合分配算法，首先使用比例公平算法给蜂窝用户分配资源，然后使用启发式的贪婪算法给D2D 用户分配复用资源，割裂了D2D 用户和蜂窝用户在资源分配时的联系，且没有模式选择方案，因此对系统性能提升作用不大。文献[8]将D2D 资源分配问题建模成一个整数非线性最优化问题，并通过贪婪和启发式算法对该问题进行了求解，得出的结果可以使D2D 用户与蜂窝用户的SINR 之和达到最大，从而达到小区信道容量最大的目的。该方案虽然可以达到最优，但是需要逐一计算小区内的蜂窝用户和D2D 用户的SINR，算法复杂度较高，效率较低。

针对上述文献的不足，在此提出了联合资源分配和模式选择的算法，提高D2D 通信模式的灵活性和空间复用率。

2 系统模型

系统模型如图1 所示。考虑基于正交频分多址OFDMA （orthogonal frequency division multiple ac cess）支持的单小区混合D2D 通信蜂窝网络模式。由于下行通信基站功率较大会对D2D 用户造成较大干扰，因此考虑小区共享上行链路资源。假设链路是完全信道状态信息。小区内有M 个随机分布的蜂窝用户（cell users）组成集合Cu=｛Cu1，Cu2，…，CuM｝；小区内有N 对随机分布的D2D 用户（D2D users）组成集合Du=｛Du1，Du2，…，DuN｝；D2D 对中的发射端、接收端分别记为DuT_i，DuR_i（即第i 对D2D 中的发射端、接收端）；系统资源块个数为K个，组成集合为Rb=｛Rb1，Rb2，…，RbK｝，资源块个数不少于蜂窝用户个数，即K>=M；基站BS（base station）位于小区中心，各信道服从瑞利衰落模型。

图1 系统模型Fig.1 System model

在引入D2D 通信之前，蜂窝用户的信干燥比SINR（signal to interference plus noise ratio）为

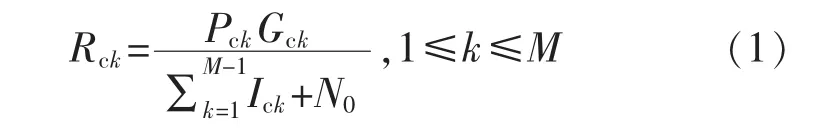
式中：Rck为只有第k 个蜂窝用户通信时的SINR；Pck为蜂窝用户的发送功率；Gck为蜂窝链路的信道增益；Ick为小区内干扰；N0为高斯白噪声。此时，系统吞吐量为

式中：ω 为频谱资源块的带宽。

引入少量D2D 用户之后，由于用户较少，则按照文献[9]为D2D 用户预留正交频谱资源是完全满足的，而且这种情况除了能提高频谱利用率外，还能有效地避免2 种用户之间的干扰。但是这只适用于D2D用户很少的情况，现实情况往往不是这样。此时蜂窝用户的SINR 和吞吐量同上。D2D 用户的SINR 为

式中：Rdk为D2D 用户的SINR；Pdk为D2D 中的第k个用户的发送功率；Gdk为D2D 链路的信道增益；Idk为小区内干扰。D2D 用户的吞吐量为

则小区总的吞吐量C 为

D2D 通信负载增加到一定程度，预留的频谱资源不足以满足正交D2D 用户，坚持正交模式则频谱利用率得不到提升，故使D2D 用户复用蜂窝用户的上行频谱资源。此时蜂窝用户的SINR 为

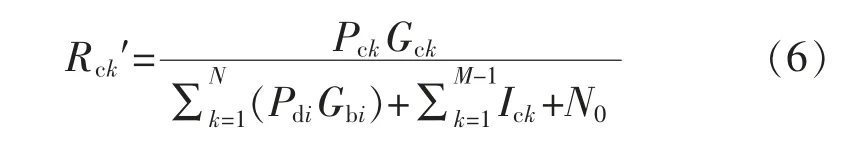
其中 1≤i≤N，1≤k≤M

吞吐量为

D2D 用户的SINR 为

其中 1≤i≤M，1≤k≤N

吞吐量为

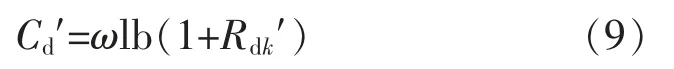
此时，小区总吞吐量为

该系统的优化目标是在保证蜂窝用户和D2D用户的服务质量的前提下最大化吞吐量，最小化各用户之间的干扰，则在此采用的约束条件为

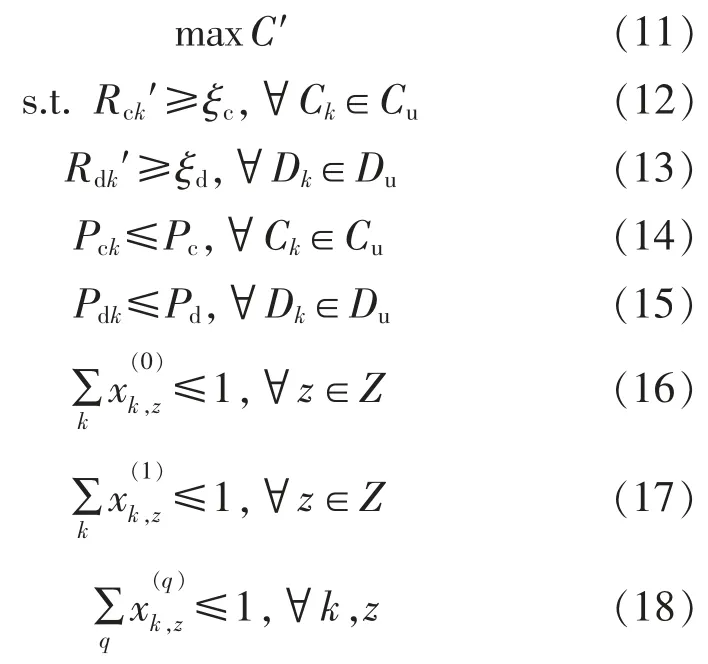
式（11）为最大化吞吐量；式（12）和式（13）设定最小接收信干燥比阈值，以确保用户能正常通信；式（14）和式（15）通过设定功率阈值，有效抑制干扰，保证用户服务质量。该约束容易陷入局部最优而难以找到全局最优解，鸟群算法BSA（bird swarm algorithm） 具有优于大多数启发式算法的跳出局部最优解的能力及稳定性[10]。因此，决定采用一种生物启发式算法——鸟群算法，完成这部分工作。

3 鸟群算法

3.1 基本原理

2015 年由Meng Xian-bing 提出的鸟群算法BSA，是计算机智能领域中一种生物启发式智能优化算法。该算法模拟鸟群觅食行为、警觉行为、迁移行为，同时具有粒子群算法和微分进化算法的优点，搜索效率较高而且稳定性较好。算法中，每个虚拟鸟类的位置就代表了问题中的一组潜在解，其分散搜索的方式有利于保持其种群多样性，避免陷入局部最优解。计算鸟群的社会行为可以简化为以下理想规则：

规则a每只鸟可随机选择警惕行为或觅食行为。

规则b选择觅食行为时，每只鸟可以迅速记录和更新自身先前寻找食物的最佳位置，鸟群也将更新群体的食物最佳位置，而且此信息可以在整个鸟群实时共享。

规则c选择警觉行为时，每只鸟尝试向种群的中心移动，这种行为受种群间竞争的影响，食物储备多的鸟比储备少的鸟有更大的概率接近种群中心。

规则d每只鸟会周期性地飞向新的位置。当鸟飞向新的位置时，其身份会在生产者与乞讨者之间转换。生产者即为储备食物最多的鸟，对应的储备食物最少的为乞讨者，其余鸟类则在生产者和乞讨者之间随意选择。

规则e生产者会主动寻找食物，乞讨者则随意跟随一个生产者寻找食物。假设N 只虚拟鸟在t时刻的位置为，在D 维空间内飞行和寻找食物。

鸟类的具体行为如下：

（1）觅食行为

规则a 是一个随机决定。如果均匀随机数rand（0，1）小于常数P（P∈（0，1）），则鸟会选择搜寻食物，否则继续警惕行为。

规则b，每只鸟会根据自身经验和种群经验寻找食物。描述为

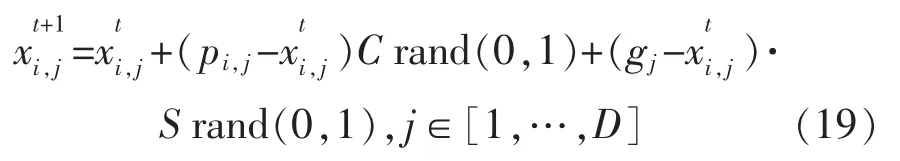
式中：rand（0，1）为0 与1 之间的独立随机数；C 和S分别为认知系数、社会加速系数；pi，j为第i 只鸟更新前的最佳位置；gj为再次更新之前种群的最佳位置。

（2）警觉行为

规则c，每个鸟不能直接移向种群中心，而是在与其它鸟类的竞争中尝试移向种群中心。其行为的数学描述为

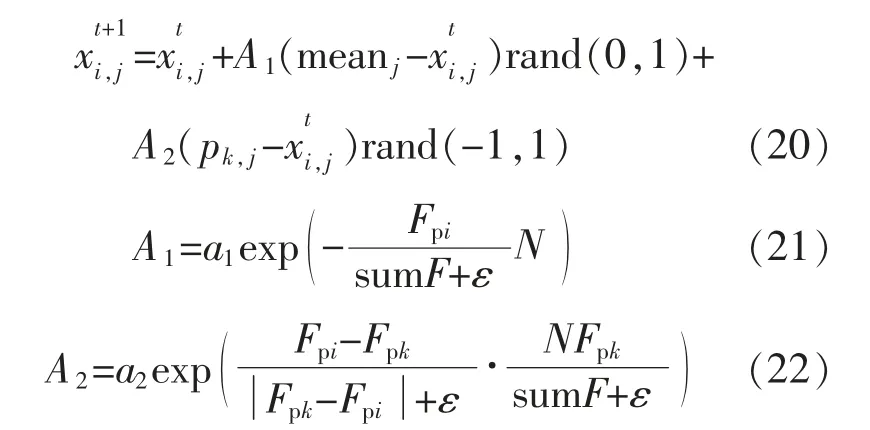
式中：k 为1～N 正整数，且k≠i；a1，a2为正常数，且a1，a2∈［0，2］；Fpi为第i只鸟的个体最佳适应值；sumF 为群体的最佳适应值之和；ε 为计算机可表示的最小常数，用于避免“0 除”错误；meanj为第j 代整个种群的适应度平均值。

（3）飞行行为

鸟类会因为逃避天敌、觅食或其他原因而进行飞行活动。当它们到达一处新领域，将再次觅食。其中，生产者主动寻找食物，乞讨者则跟随生产者搜寻食物。根据规则d，可以明确种群中鸟类个体自己的角色，且生产者和乞讨者行为的数学描述为

其中

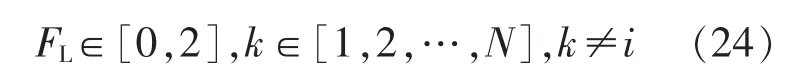
式中：randn（0，1）为标准高斯分布随机数；FL为乞讨者跟随生产者觅食的概率。另假设鸟类定期飞往另一地觅食的周期为Fq。

鸟群算法在初始化时是连续的。作为解决混合整数非线性优化问题的更好方法，首先要将问题转化为连续的问题。每个粒子的位置代表一个模式选择和子信道分配问题的解决方案，构成由2×N 个实数元素组成的向量，每个元素在0 和1 之间。每个信道对应向量的2 个元素即哪个用户采用哪种模式。对于Z 个信道和M 只鸟，第m 只鸟的位置为

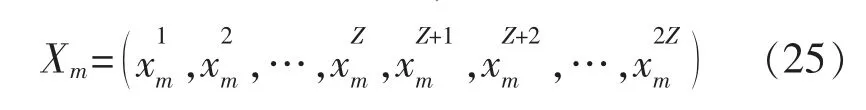
在此，信道z 最多有2 种模式的用户可供选用：在1～Z 之间的用户为蜂窝模式，在（Z+1）～2Z 之间的用户为D2D 模式可以表示采用蜂窝模式的占用信道z 的用户索引； 类似的表示采用D2D 模式的占用信道z 的用户索引值是离散的，而经过BSA算法处理的是连续的。为了使适应于将通过执行以下操作离散化：

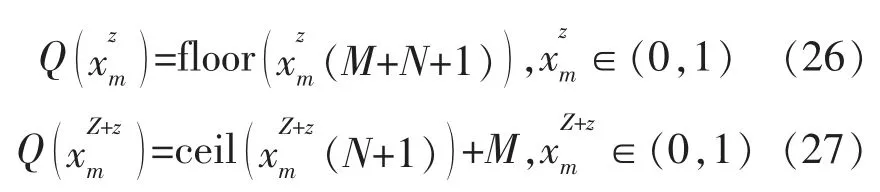
对于约束（12）和约束（13），在此引入一个惩罚函数。如果用户速率比最低要求速率高，则其对提升系统吞吐量有益不惩罚，函数值为0，反之则惩罚有效。为了能确保剔除不能提升吞吐量的用户，对函数值做平方处理。对于约束（14）和约束（15），假设基站的功率是平均分配给各个子信道的。（在此暂不考虑功率控制）

3.2 算法流程

针对所采用的通信模型，结合系统性能指标，适应度函数F（x）为

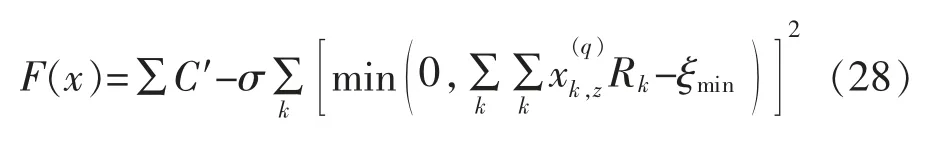
式中：σ 为惩罚因子；Rk为用户速率；ξmin为最低要求速率。

鸟群算法优化模型参数的流程如图2 所示，具体流程描述如下：

图2 鸟群算法流程Fig.2 BSA flow chart

步骤1初始化鸟群算法各参数，每个个体对应一组优化参数；

步骤2计算各个体的目标适应度值，初始筛选非劣解，从中选出最优解；

步骤3根据鸟群算法对应的更新策略，对种群进行更新；

步骤4计算新种群的适应度值，判断个体的身份形成新的非劣解，与之前的解对比，剔除重复个体，更新最优解；

步骤5判断是否满足循环终止条件，若满足则输出最优解，否则转至步骤3。

4 仿真试验及分析

4.1 仿真参数

为了验证所提算法的有效性，用MatLab 在LTE支持的单小区蜂窝系统的场景中进行系统仿真。基站位于小区中心，4 个随机分布的蜂窝用户和4 对D2D 对，D2D 对之间的距离小于50 m。鸟群算法参数设置： 群体大小M 为30 只鸟，迭代数T 为100次，其他主要参数设置见表1。

表1 鸟群算法参数的设置Tab.1 BSA setting parameters

4.2 仿真结果及分析

鸟群优化算法的仿真如图3 所示。设置最低要求速率为1000 kb/s 后执行算法，由图可见，优化过程在迭代100 次的过程中跳出局部最优解3 次，最后找到近似的全局最优解。它反映了鸟群算法具有良好的全局优化能力、处理资源分配和模式选择问题的能力。

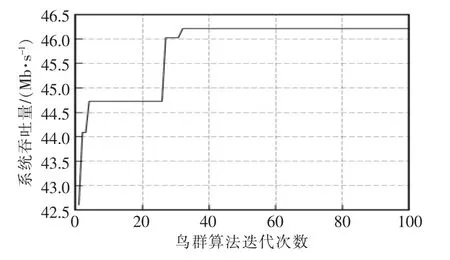
图3 鸟群算法仿真Fig.3 Bird swarm algorithm optimization simulation

不同速率、 不同方案吞吐量的对比如图4 所示。图中对比了资源分配和模式选择问题的3 种不同解决方案：throughput-PSO 曲线对应于文献[11]完成的解决方案，即标准粒子群算法处理模式选择和资源分配问题的仿真结果；throughput-OS 曲线对应于文献[9]实现的解决方案，即粒子群算法处理正交分配资源后的模式选择问题的仿真结果。在最小速率为2100 kb/s 之前，该算法优于2 种解决方案。在高速率下，优化不如其他2 种算法好。然而，由于其在低速率下的显著优势和跳出局部最优的能力，该算法具有更好的应用前景。

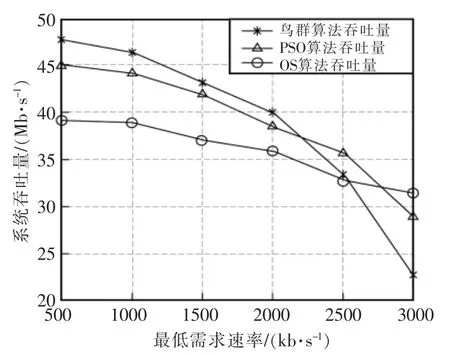
图4 不同速率不同方案吞吐量的对比Fig.4 Comparison of throughput of different rates and schemes

5 结语

聚焦行业热点问题，针对D2D 的巨大发展潜力及其与蜂窝网络通信在资源分配、通信干扰等方面存在的矛盾，结合现有文献中已有的研究基础，提出综合考虑资源分配和模式选择的基于鸟群算法的联合算法。新算法可较大程度地缓解D2D通信与蜂窝网络的矛盾，并在不影响蜂窝网络用户体验的前提下，在一定范围内提高频谱利用率，增加系统吞吐量，降低延迟；通过仿真试验也印证了BSA 优于对比的几种方案。在此通信模型暂未考虑动态功率控制，未来的研究方向可以在此基础之上结合功率控制对系统进行改进，提高系统性能。