基于控制系统工作原理的视线角速度获取方法

刘浩伟，张卫华，王 兴，伍玲玲，吴丹丽

(1. 中国航天科技集团有限公司 红外探测技术研发中心，上海 201109； 2. 上海航天控制技术研究所，上海 201109)

0 引言

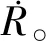
本文基于角跟踪原理推导了视线角速度方程，建立了3种视线角速度获取模型，利用卡尔曼滤波方法对3种模型进行了仿真计算，并对其有效性进行了对比分析。

1 导引头角跟踪原理

1.1 坐标系定义及符号约定

图1为典型红外导引头目标跟踪示意图。定义弹体坐标系OM-XMYMZM：坐标原点OM为弹体质心；OMXM轴为弹体纵轴，指向目标为正；OMZM为弹体俯仰轴；OMYM为弹体偏航轴；三轴方向符合右手定则。弹体坐标系绕弹体俯仰轴和偏航轴旋转得到导引头光轴坐标系OP-XPYPZP。定义视线坐标系OS-XSYSZS：原点OS取在平台旋转中心处；OSXS为弹目视线方向，指向目标为正。

图1 红外导引头目标跟踪示意图Fig.1 Schematic diagram of infrared seeker target tracking

1.2 导引头角跟踪原理

(1)

因探测器输出失调角[εyεz]都是小角度，故可做小角度近似sinεy≈εy，cosεy≈1，且将多于2个正弦项的乘积近似为0，得到角跟踪简化方程为

(2)

2 视线角速度获取数学模型

2.1 直接微分法模型

2.2 基于马尔科夫模型的视线角速度获取模型

假设目标做机动运动，则目标的随机加速机动可被视为修正的瑞利-马尔科夫过程。此处，目标加速度采用零均值一阶时间相关模型。考虑方位与俯仰方向的交叉耦合，可将目标机动模型表示为

(3)

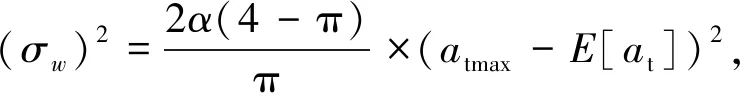
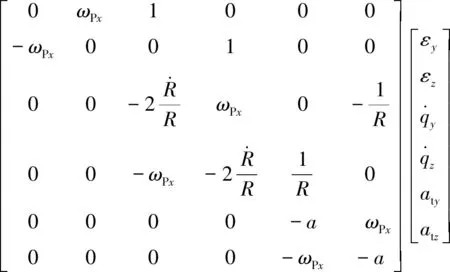
(4)

式中：asx，asy，asz为弹体运动加速度。

角跟踪系统的量测值为视线角速度εy,εz，量测方程为

(5)

式中：ny，nz为探测器量测噪声，可近似为白噪声。

2.3 基于控制系统工作原理的弹目视线角速度获取模型

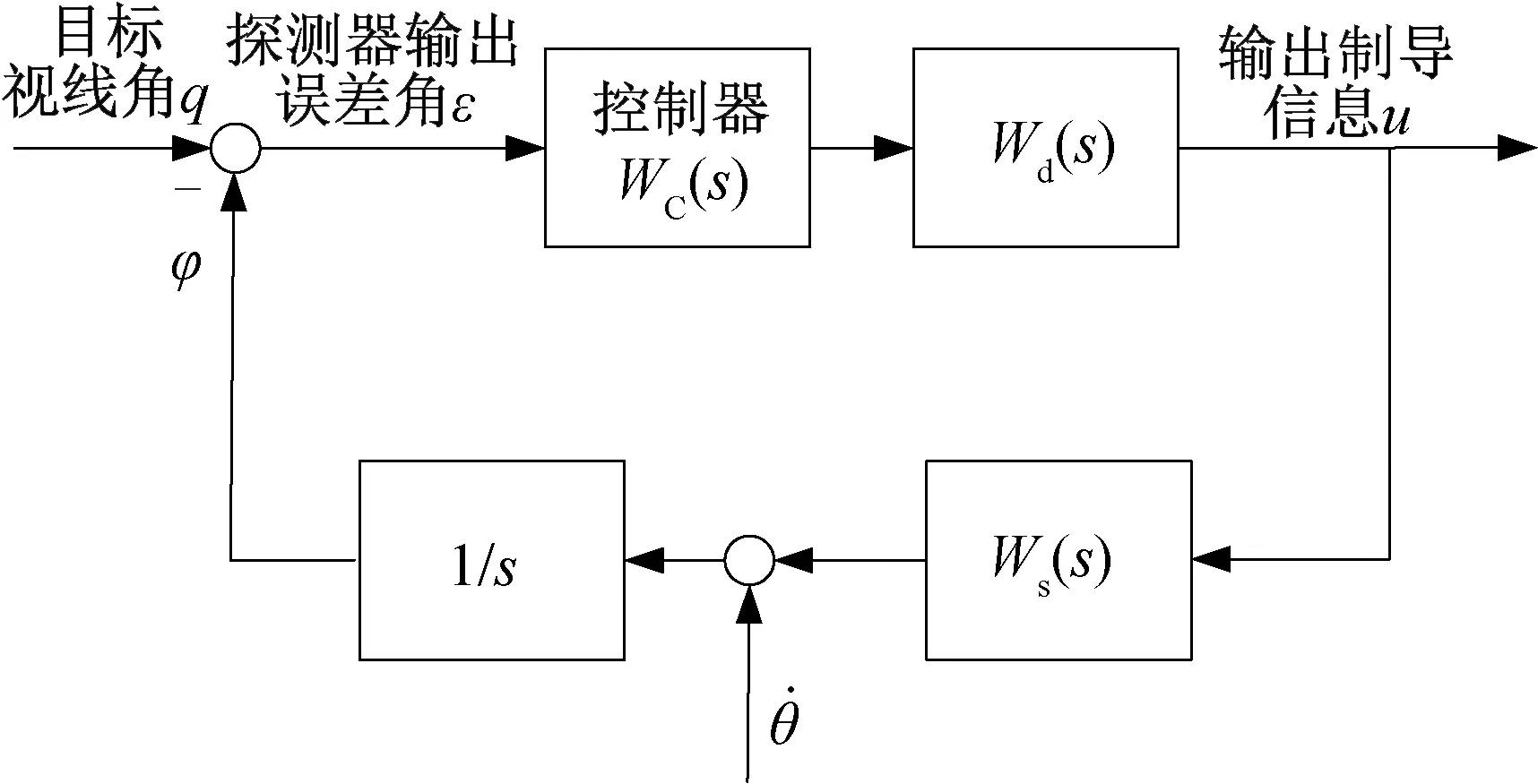
图2 红外跟踪回路简化结构图Fig.2 Simplified structure diagram of infrared seeker angle track loop

推导输出制导信息过程为

(6)

得到导引头输出制导信息为

(7)

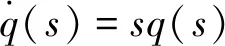
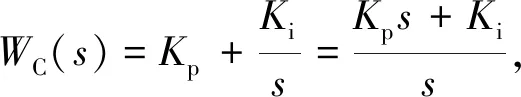
推导在此模型下探测器误差角ε与目标视线角q的关系为

(8)

(9)

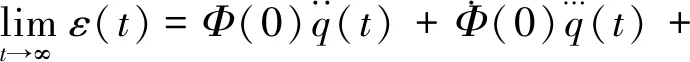
(10)

忽略q(t)的三阶以上导数较小，认为是误差项，可得

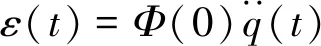
(11)

由式(10)可知，当设计的控制器满足Φ(0)很小时，探测器输出的失调角ε(t)可以很小，推导弹目视线角加速度公式为

(12)

将上式与角跟踪方程联立，建立状态方程与量测方程为

(13)

(14)

3 仿真结果与分析

3.1 卡尔曼滤波算法

作为一种线性递推最小方差估计方法，卡尔曼滤波算法以其广泛的适用性在多个工程领域发挥重大作用。卡尔曼滤波算法是获得系统状态最优估计的有效方法，能根据不同测量量估计出无法直接测量的变量。在陀螺的输出信号中引入卡尔曼滤波，从概率统计最优的角度估算出陀螺角速度误差并进行补偿，可实现高精度跟踪和稳定[8-9]。

系统的状态方程和量测方程为

(15)

式中：Xk为状态变量；Wk为系统噪声；Vk+1为量测噪声；φk+1,k为系统状态转移矩阵；Γk+1,k为噪声输入矩阵；Hk+1,k为观测矩阵。

得到自适应卡尔曼滤波算法为

(16)

式中：Pk+1,k为一步预测误差方差阵；Rk+1，Qk为系统噪声方差阵，Rk+1=E[Vk+1(Vk+1)T]，Qk=E[Wk+1(Wk+1)T]；Gk+1为滤波增益矩阵；Pk为估计误差方差阵。

3.2 仿真结果与分析

目标静止不动，弹体以3(°)/Hz的角速度摆动时的测试结果如图3所示。

图3 目标静止时弹目视线角速度Fig.3 Line-of-sight angle rate for stationary target

目标往返运动时的测试结果如图4所示。

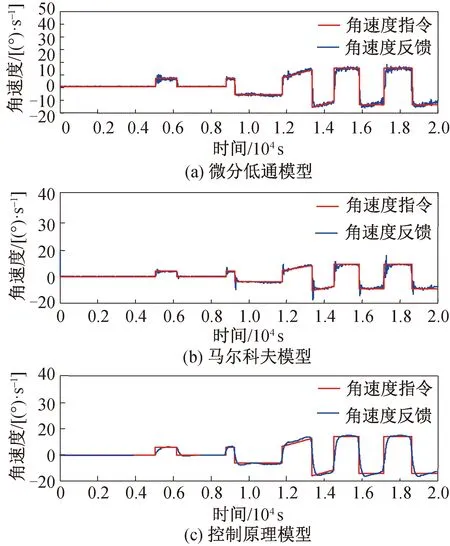
图4 目标往返运动时弹目视线角速度Fig.4 Line-of-sight angle rate for maneuvering target

分析图3，4曲线可以发现：微分法带来的角速度噪声太大，尽管加上低通滤波，可适当降低噪声，但难以消除弹体扰动影响，实际应用受限；基于马尔科夫模型的弹目视线角速度提取算法需要弹目距离信息和弹目接近速度信息，且受限于建立的马尔科夫模型的准确度，实际应用受限；基于控制原理的弹目视线角速度提取算法实现简单方便，不需要距离信息，仅需要利用陀螺和探测器失调角，过渡过程平稳，快速性满足使用要求，角速度稳定精度达到0.05(°)/s以内，满足弹体制导指标要求。

4 结束语

本文对红外导引头视线角速度提取方法进行了研究，比较分析了直接微分法、基于马尔科夫模型的方法和基于控制系统工作原理的方法3种弹目视线角速度提取方案。微分法需要对陀螺输出和探测器失调角微分输出进行传递函数匹配，并进行滤波，难度较大，工程实现复杂；基于马尔科夫模型的弹目视线角速度提取模型需要获得弹目距离信息和弹目接近速度信息，但因红外导引头无法获得这些信息，故该模型在红外导引头中的应用受到限制。本文提出将角跟踪系统设计成二阶无静差系统，将由控制系统工作原理推导的失调角与弹目视线角加速度成正比这一结论和由角跟踪原理获得的弹目视线角速度提取基本模型进行结合，提出了基于控制系统工作原理的弹目视线角速度提取方法。基于控制系统工作原理的弹目视线角速度获取方法在导引头中属于首次应用。该方法不依赖弹目距离信息，只需要陀螺、探测器坐标信息和控制系统模型信息，具有实现简单、运算量小、精度高的特点。实验室仿真验证弹目视线角速度精度由原来的1(°)/s提高到0.05(°)/s以内，满足使用要求。但是该方法在实际工程应用时，要对陀螺输出信息进行建模，且要尽可能准确获取控制系统模型参数，因此需要进一步研究陀螺噪声建模方法和控制系统辨识方法。