基于脉冲初值的小推力转移轨道优化研究
王旭生,施伟璜,王 伟,彭玉明
(1.上海卫星工程研究所,上海 201109; 2.上海市深空探测技术重点实验室,上海 201109)
0 引言
深空探测是当今世界航天活动的热点研究领域,是一个国家综合国力和创新能力的体现。我国已将深空探测纳入国家重大科技专项,正在实施首次自主火星探测任务,并规划了多目标小行星探测、火星取样返回、木星系及行星穿越等任务。其中,小行星探测任务的总速度增量要求大于8 km/s,由于传统低比冲的化学推进系统无法使用,因此小推力、高比冲、高可靠的电推进系统成为工程实施的优选动力形式。
在小推力作用下,深空探测器的轨道优化在本质上是一个最优控制问题。目前求解方法主要有直接法、间接法和混合法[1],它们都不可避免地需要进行初值猜测。初值猜测不仅在理论上作为算法的启动值必不可少,而且在工程应用上也是粗略优化的过程,可提供任务可行性、性能指标、各阶段大致时间节点等关键信息,为进一步优化轨道提供参考。脉冲轨道作为小推力转移轨道的初值,具有形式简单、计算方便的优点,被广泛应用于小推力转移轨道优化的求解,如:美国喷气推进实验室(JPL)基于圆锥曲线拼接法开发了MALTO软件包的初值,采用一系列脉冲替代小推力轨道[2],该方法已应用于木星冰卫星轨道器任务的轨道设计中[3];陈扬等[4]基于脉冲估算结果设计了电推进轨道,采用间接法求解燃料最优控制问题,得到了小推力的最优轨迹;李九天[5]提出了基于小推力可实现性的脉冲轨道约束,研究了基于该约束的燃料最优脉冲转移轨道设计方法;蒋小勇等[6]提出了一种基于多冲量能耗估算的任务窗口搜索方法,可用于搜索小推力任务的发射窗口。以上研究均基于单一形式的脉冲初值,在工程应用中未考虑脉冲轨道的多样性,缺少对不同形式的脉冲初值与小推力优化结果之间影响关系的分析。
本文基于小行星探测任务,以燃料最优为性能指标,提出了一种采取粒子群优化(PSO)和序列二次规划(SQP)的组合优化算法,可适应于不同形式的脉冲初值输入,并保证收敛性;设计了地球1∶1共振近地小行星2016HO3交会任务的小推力转移轨道,给出了轨道设计参数;对比分析了可用于小推力转移轨道优化初值结果的3种典型脉冲轨道,讨论了不同脉冲初值对小推力转移轨道优化结果的影响。
1 小推力转移轨道优化问题
在日心黄道惯性坐标系下,探测器典型的二体动力学方程为
(1)
式中:r,v为探测器的位置矢量和速度矢量;U为发动机的推力矢量,U=[FxFyFz];m为探测器的瞬时质量;Isp为发动机比冲;f为除发动机推力加速度之外的摄动加速度;g0为海平面重力加速度。r,v,m为状态变量,X=[rvm]。将式(1)简写为
(2)
将小推力轨道优化问题转换为寻找最优控制函数U(t),并使性能指标
J=J(tf,Xf)
(3)
达到最小,同时满足动力学方程约束条件、初末状态约束条件、路径约束条件,即
(4)
X(t0)=X0,X(tf)=Xf
(5)
ψ(U(t))≤0
(6)
2 优化数学模型
小推力轨道优化问题的最优控制描述形式会引入无明显物理意义的协态变量,导致收敛域窄,造成初值猜测困难[7]。本文基于直接法的离散思想,建立非线性规划(NLP)形式的小推力转移轨道优化数学模型。以离散节点的中点作为强制匹配点,将微分方程约束转化为残差形式的等式约束。
将整个飞行时间分为N个时间段,各节点处的时刻为
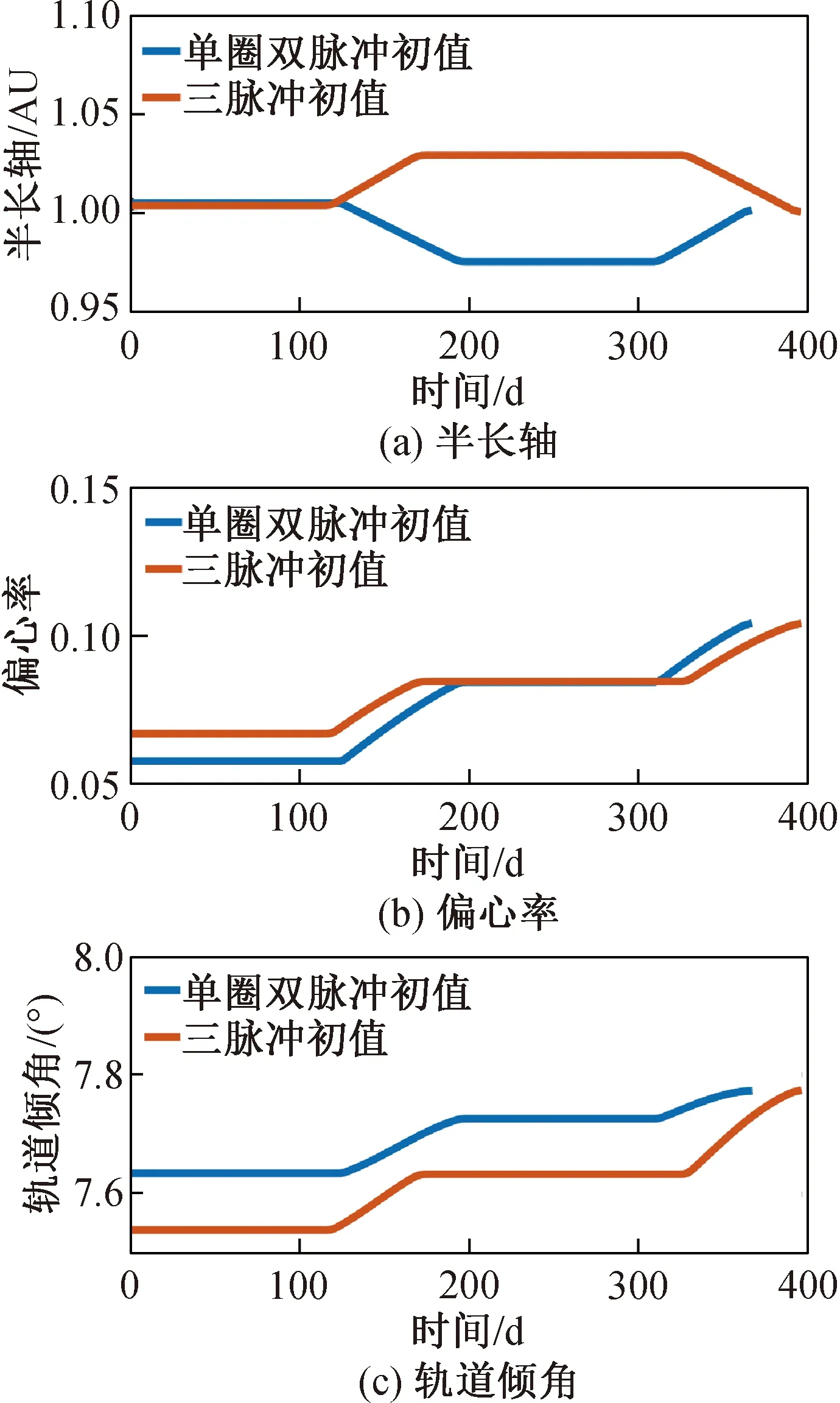
t0 (7) (8) 则S∈[0,1]。对状态变量进行三阶Hermite插值,控制变量采用线性插值。以x代表状态变量的任一分量,则 x=C0+C1S+C2S2+C3S3 (9) (10) (11) (12) 对于状态变量中任一分量均可执行上述操作。至此,连续的动力学方程约束转化为离散的7N个等式约束。 在离散形式下,初始状态与终端状态分别与出发天体和到达天体的位置速度相同,即 (13) 给定出发时间和到达时间,通过查找星历获取出发、到达天体的位置速度。末端质量自由,初始质量为发射质量,假设发射质量为m0,则 m(t0)=m0 (14) 离散形式的路径约束为各节点处的推力值小于等于最大推力值Fmax,即 ‖U(ti)‖≤Fmax (15) 以燃料最优为指标,将离散形式表示为 (16) 至此,小推力转移轨道问题优化的数学模型完成建立。寻优变量Z={t0,tf,X0,…,XN,U0,…,UN},优化指标为式(16),约束条件为式(12)~(15)。其中,约束条件和性能指标可根据具体情况进行相应修改。 传统PSO算法具有全局优化和并行计算的能力,相比于经典的基于梯度的优化算法具有更好的全局收敛性[9],但PSO算法出现早熟现象的概率较大,以致收敛于局部最优解。为此,本文通过线性减小惯性权重系数和局部学习因子,增大全局学习因子,使算法在初期具备较强探索能力,在后期又有较好的收敛性,使其在最优解附近精细搜索。本文算法主要包括以下步骤。 1) 初始化粒子群位置p和速度v,粒子位置信息包含脉冲作用时刻和脉冲作用矢量。 2) 对每个粒子用构造的位置函数Fitness进行评价,此时Fitness为总速度增量。 3) 更新每个粒子的历史最优位置pb和群体的全局最优位置gb。 4) 分别按照式(17),(18)更新每个粒子的速度和位置,其表达式为 vi+1=w·vi+c1·rand()·(pb-p)+ c2·rand()·(gb-pb) (17) pi+1=pi+vi+1 (18) 式中:w为粒子的惯性权重系数;c1为局部学习因子;c2为全局学习因子;rand()表示0~1的随机数。同时设置粒子学习速度在[-vmax,vmax]内,若更新后的速度超出边界,则取相应的边界值。w,c1,c2的更新依据为 (19) (20) (21) 式中:c为运行代数;cmax为最大运行代数。 5) 判断终止循环条件。若条件不满足,则循环执行步骤2~4;若满足,则输出结果,生成初值Z0={t0,tf,X0,…,XN,U0,…,UN}0。其中,{t0,tf}和{X0,X1,…,XN}中的位置和速度分量可直接从结果中生成,质量可基于其消耗特性按等差递减生成;{U0,U1,…,UN}0可在[0,Fmax]内随机猜测。为避免随机性对结果带来的影响,Ui0=Fmax[0.5, 0.5, 0.5]。算法相关参数设置见表1。 表1 粒子群算法参数 SQP算法是求解NLP问题的有效算法[10],但SQP算法是基于可行方向搜索的一种约束优化方法,其只具有局部优化能力,因此将SQP与PSO算法结合可充分发挥两者优势。算法的主要步骤如下。 1) 给定PSO算法搜索后生成的初值Z0,选定正定矩阵H0。 2) 求解的二次规划问题为 mindT s.t. con(Zk)+dTcon(Ζk)≤0 (22) 式中:obj为目标函数;con为约束;dk为搜索方向,当‖dk‖<10-6时,迭代结束。 3) 更新Zk+1=Zk+αkdk,其中αk由线性搜索确定。 4) 修正Hk,使Hk+1保持正定。 5) 判断是否满足迭代终止条件:若迭代次数超过2 000次或‖dk‖<10-6,则迭代结束;否则重复步骤2~4。 为便于计算,初值生成过程和优化求解过程的寻优变量均进行归一化处理。组合优化算法的流程如图1所示。 图1 组合优化算法流程Fig.1 Combinatorial optimization algorithm flow 2016HO3是2016年发现的1颗阿波罗型地球1∶1共振近地小行星,其日心轨道周期与地球公转周期呈现1∶1的关系。虽然2016HO3为绕日小行星,但是其相对地球的轨道较稳定,因此被称为地球的第2个月亮。该小行星具有独特的探测价值,是我国小行星探测任务的首要备选目标,其轨道参数见表2。表中:AU为天文单位;MJD为约化儒略日。 分析不同初值对优化结果的影响。假设探测器的发射质量为1 500 kg,发射日期在2022年1月1日至2024年1月1日之间,飞行时间小于700 d。发射C3(离开地球引力影响球时与地球相对速度的平方)不大于20 km2/s2,2016HO3交会任务的发射C3等高线如图2所示,发射时间从2022年1月1日开始。由图可见:若仅从发射C3的角度考虑,则每年有4个发射窗口,平均每季度出现1次波谷,分为长转移和短转移,两者交替出现。其中,长转移时间约为380~550 d,短转移时间约为50~200 d。 表2 2016HO3小行星轨道参数(MJD=58 000.0) 图2 发射C3等高线Fig.2 Contour line of launch C3 假设小推力大小为120 mN,发动机比冲为3 500 s,推力大小和方向可调。选取单圈双脉冲、三脉冲、多圈双脉冲3种典型的脉冲初值轨道。将转移轨道等时间间隔离散为150个轨道段,经PSO算法搜索后的初值轨道参数及经SQP算法优化后的小推力轨道参数见表3,由表可得: 1) 3种初值轨道优化后得到了2022年11月29日和2022年5月28日这2个发射窗口,其中三脉冲初值和多圈双脉冲的初值总速度增量差距最大,但优化结果最为接近。 2) 优化轨道和初值轨道的发射时间与飞行时间具有强耦合关系,提供的初值飞行时间越长,优化得到的结果飞行时间也越长。SQP算法只是局部优化,因此优化轨道与初值轨道的飞行时间非常接近。 表3 2016HO3小行星交会任务轨道优化结果 3) 3种形式的脉冲转移轨道总速度增量差距最大达58%,而3种小推力转移方案燃料消耗差距不超过6%。由此可见,本文算法对初值的敏感度小,具有一定的全局优化能力。 各初值对应的小推力转移轨道的控制曲线如图3所示。图中,推力方向以黄经、黄纬表示。 图3 不同初值的最优控制Fig.3 Optimal control curves of different initial values 由图3可见: 1) 小推力发动机基本符合满推或关机的形式,即为Bang-Bang控制的小推力轨道最优控制形式[11]。 2) 最优小推力转移轨道总体上存在2个主推进段,不同的脉冲轨道初值对应的最优控制曲线的差异主要体现在推力器开关机时刻的不同上。 3) 对于不同初值对应的优化结果,其推力方向的变化在相位上有明显差别,可看出2个发射窗口对应2种推力变化形式。 4) 从飞行时间来看,多圈双脉冲初值优化得到的小推力转移方案在第2个推进段关机后有约10 d的自由飞行段。由此可见,三脉冲初值具有更优的性能。 图4 燃料最优小推力转移轨道根数变化Fig.4 Time histories of fuel-optimal low-thrust transfer orbital elements 单圈双脉冲初值和三脉冲初值对应的小推力转移轨道根数变化过程如图4所示。由图可见:对应于日期为2022年11月29日的发射窗口,发动机的工作序列为“先长后短”;对应于日期为2022年5月28日的发射窗口,发动机的工作序列为“先短后长”。11月的发射窗口与5月的发射窗口相比,当探测器从地球出发时,前者为小偏心率大轨道倾角,后者为大偏心率小轨道倾角。从半长轴变化趋势来看,前者为先减小后增大,后者为先增大后减小。 为解决小推力轨道优化未考虑脉冲初值多样性的问题,利用不同形式的脉冲轨道初值对小推力转移轨道优化结果的影响进行了研究,提出了能适应不同脉冲初值的组合优化算法,以我国深空探测规划背景任务中的小行星探测任务为例进行了仿真分析。针对近地小行星2016HO3交会任务,以3种典型的脉冲轨道优化得到了3种具体的小推力转移轨道方案和2个发射窗口。其中,三脉冲轨道初值与多圈双脉冲轨道初值对应的优化结果主要体现在开关机时刻的不同,单圈双脉冲初值与三脉冲初值、多圈双脉冲初值的优化结果主要体现在推力方向变化的差异,3种初值轨道对应最优小推力轨道燃料消耗量差距不超过6%。研究结果表明:本文算法对初值的敏感度低,能收敛于Bang-Bang最优控制形式;不同初值对小推力轨道的整体性能指标影响较小,但开关机时刻和推力方向的变化会产生较大差异,从而得到不同的最优控制曲线。该研究成果对小推力轨道优化初值的选取、我国未来小行星探测任务的工程实施具有一定的参考价值。由于本文未对2个窗口的控制策略进行优劣性分析,且优化模型仅以燃料消耗作为评价指标,未考虑轨道设计中飞行时间、控制误差、多体模型等其他重要参考因素,因此后续将综合考虑多种评价指标,进一步优化设计。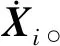

3 基于PSO和SQP的组合优化算法
3.1 PSO算法搜索脉冲初值
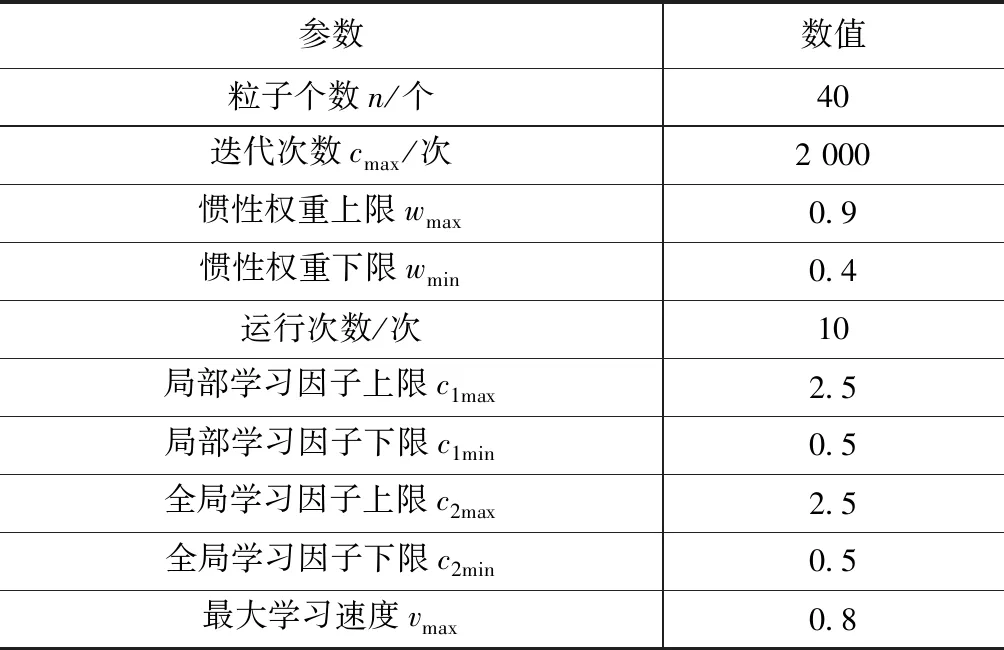
3.2 SQP算法求解NLP问题

4 近地小行星2016HO3交会任务




5 结束语

