基于解耦式EHB的多电机再生制动策略设计＊

徐国栋 余卓平 熊璐 潘光亮 于洋

（1.同济大学，上海 201804；2.上海同驭汽车科技有限公司，上海 201806）

主题词：电子液压制动系统 再生制动 多电机驱动

1 前言

再生制动功能已成为汽车行业的一个重要研究方向。卢东斌等[1]研究了电动汽车永磁同步电机的最优能量回馈控制策略，明确了动力电机最优回馈力矩动态变化的特性；姜标等[2]研究了基于制动力变比值优化分配算法的电动汽车再生制动控制策略，可优化前轴制动力矩分配；Guoqing Xu等[3]基于阀控的电子液压制动系统设计了一种再生制动策略，并进行实车试验，取得了较好效果；Ohkubo等[4]使用了一种基于高压蓄能器方案的电子液压制动系统进行试验，实现了类似功能。但由于电子液压制动技术还不够成熟，目前市场上大规模应用的仍是并联式再生制动策略，无法充分发挥回馈潜能。

解耦式电子液压制动（Electro-Hydraulic Braking，EHB）系统可进行协调式的电液制动力分配，为制动系统控制提供了新的自由度，能够实现液压制动力矩对电机动态变化特性的补偿。因此，基于解耦式EHB的再生制动策略将能充分发挥电机的最优回馈能力。

目前，针对解耦式EHB的电液复合制动策略研究已有较多，基于单电机特性约束和车辆动力学约束特性的分配策略备受学者青睐。近来，多电机驱动方案逐步进入研究人员的视野。这类驱动方案有分布式驱动方案和集中式双电机驱动方案两种主要形式，均能通过合适的能量管理策略最大程度地发挥其回馈潜力。

本文研究多电机驱动方案的系统特性，提出一种基于解耦式EHB的多电机再生制动策略，以提高车辆的舒适性和经济性，并兼顾安全性。

2 系统模型

2.1 车辆底盘拓扑结构

含有解耦式EHB系统的分布式驱动方案和集中式双电机驱动方案底盘拓扑结构如图1、图2所示，两种方案液压制动系统的组成相同，电制动部分均可通过多电机协同输出最优回馈力矩，因此，可以设计相同的再生制动控制策略。其基本思路是，基于串联式电液复合制动力矩分配方法分配电机回馈扭矩和液压制动力矩，电机回馈扭矩通过效率最优方法分配至各组电机。

图1 分布式驱动方案

图2 集中式双电机驱动方案

2.2 单自由度纵向动力学模型

对于车辆的纵向动力学问题，ECE R13-H[5]限制了车辆的前、后轴制动力矩分配，以避免车辆因轮胎抱死打滑造成失稳。但是，随着ABS的普及，事实上，这一限制已显得不再必要。GB 21670—2008中指出，对满足特定条件的车辆，可适当延后其他制动能源的制动输入，使电力再生式制动系单独起作用[6]。因此，可不对基于车辆前、后轴的动力学特性约束作过多考虑。此时，整车模型可简化为单自由度纵向动力学模型[7]，制动系统模型可简化为液压主缸-轮缸模型[8]：

式中，Fb为车辆总制动力；Fp为因液压制动产生的制动力；Fm为因电机制动产生的制动力；p为EHB输出液压；p0为轮缸启动液压，Scf、Scr分别为前、后轮轮缸活塞面积；rf、rr分别为前、后轮制动器作用半径；Rf、Rr分别为前、后轮轮胎半径；ηf、ηr分别为前、后制动器制动器效能因数；Tm为电机输出扭矩；i为传动比；Fair为空气阻力；Fslope为坡道阻力；Fnoise为外界作用于车辆的噪声力；A为车辆迎风面积；Cd为风阻系数；R为车轮半径；v为车速；m为车辆质量；θ为坡度。

2.3 EHB系统模型

本文所讨论的EHB系统[9]如图3所示，因其解耦特性而能够实现一定裕度范围内的液压调整，能够输出不低于主缸p-v特性曲线且不高于EHB最大建压能力（由EHB电机峰值力矩限制）的液压力，如图4所示。

图3 EHB结构简图

图4 EHB理论液压调节范围

另一方面，由于系统的踏板感觉要求，不可能实现在任何踏板开度下均输出最大液压力，通常存在一条较为理想的踏板感觉曲线，如图5所示[10]。

图5 一种较为理想的踏板感觉曲线

在电液复合制动系统中，在再生制动模式下，不可能使用电机进行驱动抵消EHB产生的制动力，因此，EHB输出液压力应介于制动系统p-v特性曲线和理想踏板感觉曲线对应的液压力之间，如图6所示。

图6 EHB液压调节范围

动态响应方面，这类EHB系统方案普遍由位移传感器、电机、传动机构和建压单元组成，可采用动态响应特性仿真方法进行模拟[11]。基于EHB的动态响应模型可近似为二阶线性系统模型[12]，并引入压强计算公式：

式中，x为主缸位移；mehb为EHB系统质量；f为系统摩擦力；Fehb为EHB输出力；Fs为主缸压力；c为系统阻尼；k为系统刚度；Smc为主缸面积；Tehb为EHB电机输出扭矩；iehb为EHB传动比；rehb为齿条分度圆半径。

为避免仿真数据溢出造成错误，增加约束条件：

式中，lmc为主缸最大位移。

2.4 电机模型

采用标定“转速-转矩-效率”曲线的方法确定电机效率模型，对非试验数据，采用线性插值方法确定。电池和电机控制器在良好工作区间内效率差异较小[13]，可以通过联合标定，以电机效率代表动力总成效率。一种电机的效率特性曲线如图7所示。

图7 一款永磁同步电机的效率特性

电机充、放电功率Pchr、Pdischr分别为：

式中，ω为转速；η为效率。

动态响应方面，由于当前电机控制精度普遍较高，响应较快，一些整车企业在标定过程中，常取3%作为精度基本要求，1 kN·m/s作为响应速度基本要求，由此，本文将电机动态模型简化为一阶惯性系统：

式中，Tm_cmd为电机目标输出扭矩；a为惯性时间常数。

3 控制策略设计

3.1 制动意图解析

制动意图分为滑行制动（完全松开制动踏板和油门踏板）和行车制动（踩下制动踏板）两种工况。

新能源汽车滑行制动一般通过动力电机实现，以实现能量回收，存在电机制动低速退出的风险。因此，使用EHB系统的新能源汽车低速工况下可在一定程度上补充制动液压力，弥补电机扭矩退出造成的制动力减小。

行车制动过程则可采用串联式电液复合制动分配策略。在制动意图解析时，需保证制动力不小于滑行制动的制动力。因此，在踩下制动踏板行程较浅时，所产生的制动液压力较图5所示的理想踏板感觉曲线对应的制动液压力更高，制动意图解析如图8所示。

图8 制动意图识别曲线

3.2 电液复合制动力矩分配策略设计

电液复合制动力矩分配策略可使用如图9所示的状态机进行描述。

图9 再生制动模式切换策略

3.2.1 再生制动运行模式

在运行模式下，采用串联式电液复合制动，基于回馈功率最优要求进行力矩分配：

式中，Tehb_cmd为EHB目标输出扭矩；Tcmd为总目标制动力矩；Tehb_min为EHB最低输出液压等效制动力矩；Tm_bmax为电机最大回馈力矩。

3.2.2 再生制动退出模式

在退出模式下，基于舒适性最优要求进行力矩分配。在此过程中，需要将电制动切换为液压制动，由于电机响应速度高于液压系统，因此，可采用前馈方法利用电机回馈力矩进行液压力矩补偿，使电制动逐渐退出，确保平稳性：

式中，Tehb_cmd为EHB输出目标制动力矩；Tehb_est为EHB估计制动力矩，估计过程使用EHB动态响应模型进行。

3.2.3 再生制动关闭模式

在再生制动关闭模式下，基于安全性要求分配力矩，使用液压制动策略。令输出目标液压力等于制动意图解析的制动液压力，所有电机控制力矩输出均为零。

3.3 电机效率最优分配策略

最优分配系数定义为一个（组）电机所控制的目标扭矩在总电机目标扭矩中的占比[14]。在轮毂电机分布式驱动方案中，该系数可以指前轴2个轮毂电机所控制的目标力矩占比；在双电机集中式驱动方案中，该系数可以指其中一个电机所控制的目标力矩占比。

计算电机输入功率如图10所示，为使电机输入功率最小，经过效率加权后，采用数值计算的方法确定双电机的最优分配系数，如图11所示。

图10 电机输入功率

3.4 信号处理算法

受传感器精度、路面阻力变化、风阻变化等干扰，实际测量的信号往往存在一些扰动。本文采用卡尔曼滤波方法[15]处理电机转速波动：

式中，Tcycle为运算周期；vest为估计车速；P为估计数据协方差；Kg为卡尔曼增益；Qk、Rk分别为系统方程和测量过程的协方差；ωm为电机转速。

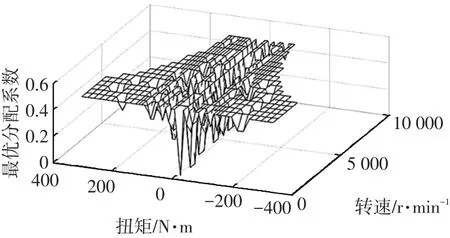
图11 电机最优分配系数

3.5 防抱死约束

如2.2节所述，需满足GB 21670—2008相关条件：

a. 满足“在低附路面上制动时，符合车轴间力矩分配比例要求”或“装备有防抱制动系统”，且“由动力电池荷电状态变化等所引起电力再生式制动系输出力矩的固有变化可通过适当的相位关系自动补偿”。

b. 在必要时（路面附着条件不足），自动对所有车轮进行制动，确保达到与驾驶员操作相对应的制动强度[3]。

目前的乘用车市场上，除极少数低成本乘用车外，大多数车型都配备有ABS。且再生策略能够根据动力总成实时状态分配电液制动力矩。因此，条件a满足。

为满足条件b，需要设计再生制动功能退出策略，充分发挥液压制动能力。

路面附着条件难以估计，因此，可以采用与ABS触发逻辑相同的方式预判。为预判ABS的触发，可采用车轮角减速度阈值估计方法，确定车轮是否具有抱死趋势或减速度过大。预判标志位的计算方式为：

式中，Kω为放大系数；fω（sbrake,v,θ,m）为角加速度关系函数，可由实车试验标定获得，也可使用前文模型进行估计；sbrake为制动踏板行程。

4 离线仿真验证

4.1 仿真模型

仿真环境采用MATLAB/Simulink 2016进行搭建。为保证模拟精度，同时模拟实车ECU定时运算系统特性，设定仿真方式为离散定步长（步长为0.01 s）方式，求解器为Runge-Kutta求解方法。

仿真模型包括驾驶员模型、策略模型和系统模型。

驾驶员模型采用PID控制方法，监控车速与工况目标车速，控制油门和制动踏板开度。PID控制目标为实际速度和目标速度的误差，PID参数设置见表1。

表1 驾驶员模型PID参数

系统模型按照本文第2章进行搭建，部分参数如表2所示。策略模型按照本文第3章进行搭建。

表2 系统模型部分参数

4.2 离线仿真

4.2.1 信号滤波效果

在车辆模型中，添加了噪声模块来模拟实车运行过程的速度噪声。滤波前、后的转速结果如图12所示，可以看出，信号平滑度明显提高。

通过对转速减速度信号滤波前、后的结果（见图13）进行对比可以看出，滤波器明显减小了速度变化率峰值水平，这种输入信号对基于微分的控制算法更加友好，也能避免输出控制量产生较大震荡。

图12 电机转速变化曲线

图13 电机转速变化率曲线

4.2.2 能耗对比

在NEDC工况下，通过对比所设计再生制动策略和双电机输出相等制动力矩的控制策略（见表3）可以看出，电机输出效率得到改善，驱动耗能更少、制动馈能更多，总体能量消耗率减小。

表3 策略功耗对比

并且，在驱动过程中，对比效果更加明显。如图14所示，在NEDC工况下，电机实际运行的工况点仅覆盖电机map图很小范围。在电机特性第一象限中，主要工况点效率差异更小，最优分配带来的效率差异更低；在电机特性第四象限中，主要工况点效率差异更大，最优分配带来的效率差异更高。

图14 NEDC工况下电机运行工况点

在实际应用过程中，电机工况点将更加复杂，由此，所采用的最优分配策略将带来更大的效率提升。

4.2.3 平顺性对比

采用“加速-减速”工况进行平顺性对比，工况设置如图15所示，对比结果如图16所示。

图15 输入信号

图16 仿真过程中的加速度变化

在减速过程中，未采用前馈策略时，制动力在电机力矩退出后（第21 s）产生瞬间衰退，随着液压制动力矩逐渐提高，总加速度得以维持到目标加速度。而采用前馈策略后，制动过程中加速度较为平稳，无明显波动。

5 结束语

本文设计了一种再生制动策略，通过仿真对比，得到如下结论：

a.基于卡尔曼滤波算法，将带噪声信号进行滤波处理，减小噪声幅值，有利于芯片平台上控制算法的运行。

b. 所设计的最优电机力矩分配策略，能够使能量消耗率降低，且对于不同电机效率特性，电机工况范围内效率差异越明显，则优化效果越明显。

c.前馈式电液复合制动退出策略能够很好地减弱制动过程中的加速度突变，并在一些情况下缩短制动时间。

d. 提出的预判ABS触发的方法，可采用原有车辆所包含的车辆传感器信息进行处理，具有可行性。