车辆弯道避撞控制研究*
张佳佳 魏民祥 项楚勇 吴树凡 邢德鑫
(南京航空航天大学,南京 210016)
主题词:弯道 换道避撞 扩展卡尔曼滤波
1 前言
随着汽车向电动化、智能网联化、共享化方向发展,先进驾驶辅助系统(ADAS)为驾驶员提供了安全保障。由于车辆事故多发生在弯道、十字路口等路段,主动安全技术在特殊路段的控制显得尤为重要。
障碍物的信息采集是主动安全技术的关键技术之一。王芬芬[1]基于机器视觉提出了一种结合像素灰度值差异的边缘保持滤波算法,可较为精准地检测到障碍物信息,但计算量大,耗时长,不适用于实时检测。张瑞峰[2]建立了实时的雷达地图显示前方车辆与自车的相对速度、距离、预测的碰撞时间(Time To Collision,TTC)等,为碰撞预警控制系统提供了关键信息,但没有提出相应的控制策略。张凤娇[3]提出了一种基于模型预测控制(Model Predictive Control,MPC)的汽车紧急换道控制策略,在车辆仅采取制动措施不能避免碰撞的条件下,采用换道实现避撞,但没有考虑弯道的避撞问题。对于换道轨迹规划,国外学者提出了利用圆弧曲线[4]、贝塞尔样条曲线[5]、考纽螺线[6]等拟合轨迹,国内的戚志锦[7]采用余弦函数作为换道轨迹,并设计了模糊自适应PID控制器,但未考虑行驶路面为弯道的情况。Hatipoglu C[8]在车辆弯道行驶的研究中,确定期望横摆角和横摆角速度时考虑了道路的曲率,但在车辆换道过程中没有考虑内、外车道曲率变化的情况。
针对以上研究的不足,本文提出了一种弯道避撞控制策略,在弯道行驶中前方车辆紧急制动的危险工况下,若自车无法通过制动避开前方车辆,采用换道路径规划的避撞控制算法。基于PreScan软件搭建弯道场景模型,利用弯道安全距离模型实时判断是否处于危险工况;危险工况下,自车依据斜坡正弦函数作为换道路径,进行换道避撞;采用扩展卡尔曼滤波(Extended Kalman Filter,EKF)算法对车辆横摆角速度等关键状态变量进行实时跟踪,保证算法在满足稳定性的前提下安全避撞。
2 弯道建模与车辆状态估计
2.1 弯道建模
考虑到汽车行驶的安全性,车辆进入弯道后一般不进行加速操作,假设汽车在弯道中低速行驶,为降低道路模型的复杂度,将道路模型简化为一段圆弧,曲率中心为OC。以外侧弯道中心线l1入口为原点O1,以l1的切线为x轴,以垂直于x轴并指向OC的直线为y轴,弯道运动模型如图1所示。

图1 弯道运动模型
假设l1与l2具有相同的瞬心,l1、l2的曲率半径分别为R、r0,d为在同一弯道轨迹中两车的弧长距离,θ为车辆航向角,ye为车辆换道完成后的侧向位移,即两车道中心线间距,换道过程中沿曲率中心方向的加速度为:

沿弯道切线方向的加速度为:

式中,v为换道过程中的车速;v0为车辆初始速度;α为质心侧偏角;ac为换道过程的侧向加速度;te为换道完成时间。
2.2 3自由度模型
从本文估计车辆状态的角度出发,需要引用纵向X、侧向Y、和横摆Z 3个自由度的状态变量。因此,在线性2自由度车辆模型的基础上引入纵向运动自由度,模型如图2所示。
图2中,假设车辆是对称的,XOY是固定在车辆质心处的坐标系,规定X轴在汽车的纵向对称轴上,向前为正方向,规定Y轴在水平面内与X轴垂直,通过车辆质心O点,向左为正方向。为了便于EKF算法估计,建立3自由度车辆模型的系统状态方程为[9]:

图2 3自由度非线性车辆动力学模型

式中,r为车辆横摆角速度;k1、k2分别为前、后轮总侧偏刚度;m为汽车总质量;a、b分别为前、后轴到质心的距离;δ为前轮转角;Iz为绕Z轴的转动惯量;β为质心侧偏角。
状态变量为x(t)=(r,β,vx)T,量测方程为 y(t)=ay,控制变量为u(t)=(δ,ax)。
2.3 车辆状态估计
EKF算法是将非线性函数在最佳估计点进行泰勒展开,使该模型线性化,从而适用于各种非线性系统[10]。
建立系统状态方程及量测方程:

式中,w(t)为系统激励;v(t)为量测噪声。
设Q为系统激励噪声的协方差矩阵,R为量测噪声的协方差矩阵。分别对式(6)、式(7)的状态变量求导,得到雅可比矩阵F(t)、H(t):

设EKF算法的状态过程噪声方差矩阵为Q=diag(0.1,0.1,0.1),观测协方差为Rk=[0.001]。
3 换道路径规划与安全距离模型
3.1 换道路径规划
车辆在转向时,最易发生碰撞的部位是自车右前部与前车左后部,本文针对这种典型的碰撞情况进行了换道过程分析。
为研究需要,对车辆转向换道运动作出如下假设:
a. 自车在最大制动强度条件下已下无法避开前车;
b.自车在整个换道过程中低速行驶;
c. 自车、前车车辆尺寸和性能相同;
d. 假设双车道上只有自车和前车,两车起始位置同在外侧弯道,相邻车道上无其他车辆,且前车紧急制动;
e.仅考虑自车从外侧弯道换道至内侧弯道的避撞路径。
换道过程如图3所示,其中,tc为预碰撞时刻,xe(t)为车辆换道的纵向位移。

图3 汽车换道位置示意
本文采用斜坡正弦函数[11]作为换道路径:

xe=v·te,带入式(10)中,得到ye与t的关系(即换道轨迹),如图4所示。

图4 斜坡正弦函数换道轨迹
对式(10)进行二次求导得到换道路径的侧向加速度:

在自车转向换道过程中,考虑驾驶员反应时间对安全距离的影响较大,采用文献[12]的研究结果,选取驾驶员类型为男青年普通型,反应时间τ1=0.935 s。在危险工况下,若转向盘转角传感器在该时间段内未检测到明显变化,则默认为驾驶员未进行转向操作,车辆处于极不安全的状态,此时由换道避撞控制系统接管车辆,通过控制转向盘转角δsw完成换道操作。转向盘转角由逆动力学模型[13]计算得出:
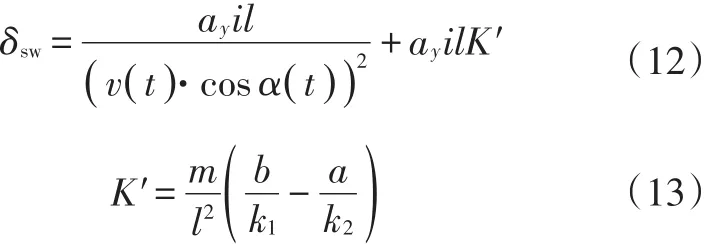
式中,l为车辆轴距;i为转向系传动比;K′为稳定性因数。
3.2 安全距离模型
为避免与前车发生侧碰及追尾,当自车检测到与前车直线距离小于安全阈值时,进行转向换道操作,两车初始的弧长距离d应满足:

式中,s0、s1分别为自车和前车运动的路程;a0为自车的加速度,其大小为沿弯道切线方向加速度与沿曲率中心方向加速度的矢量和的模长;a1为前车的加速度;L为车长;W为车宽。
由于目前车辆辅助驾驶系统采用的传感器(如激光雷达、毫米波雷达)只能采集直线距离,对弯道距离的检测较困难,故将弯道弧长安全距离转换为直线长度[14]。根据弦长公式,由图3可知该弯道模型的安全距离S为:

4 控制器设计及算法验证
4.1 弯道避撞控制器设计
弯道避撞控制器根据车载前置摄像头实时检测车道线,由传感器测得两车实际距离,根据安全距离模型计算出安全距离S,判断车辆是否处于危险工况,一旦检测到实际距离s小于安全距离S,开启转向换道控制。控制器整体逻辑框架如图5所示。由于弯道避撞过程中除换道产生的侧向加速度外,车辆还有沿弯道行驶的向心加速度ac,联立式(1)与式(2),得到避撞过程中车辆实际侧向加速度为:

式中,yd为车辆移动过程中的侧向位移。
由转向逆动力学模型得出理想转向盘转角δ0,该角度为车辆弯道行驶的转向盘转角δ1和换道避撞过程中的转向盘转角δ2的线性叠加:


图5 控制器逻辑框架
下层控制器采用PID控制,通过比较δ0与实际转向盘转角δsw的偏差,调节PID值使得δsw较好地跟踪δ0。
4.2 估计算法的虚拟验证
为验证EKF状态估计算法的有效性,在PreScan与MATLAB/Simulink环境下建立联合仿真平台,以PreScan软件的状态输出结果为实际值,将其与EKF算法的估计结果进行对比。整车的参数如表1所示,设定前车速度为36 km/h,自车速度为46 km/h。

参数车宽/m质心绕Z轴的转动惯量/kg·m2前轮侧偏刚度/kN·rad-1后轮侧偏刚度/kN·rad-1参数整备质量/kg前轮距/m后轮距/m质心至前轴距离/m车长/m取值1 480 1.50 1.50 1.08 4.43取值1.86 2 562-181.70-198.91
模拟在附着系数μ=0.85的路面进行蛇行试验,转向盘转角变化如图6所示,在第2.5~7.5 s时间段内转向盘转角做幅值为40°、周期为2.5 s的正弦变化。

图6 转向盘转角变化
图7 所示为纵向车速EKF估计值与实际值的对比,从图7可以看出,EKF算法车速估计效果比较理想,估算值与实际值最大瞬态偏差仅为0.02 km/h,相对误差为0.03%。
图8所示为横摆角速度EKF估计值与实际值的对比,从图8可以看出,EKF算法估计效果较理想,最大瞬态偏差出现在第6.8 s,偏差为0.9°/s。以上分析表明,提出的EKF算法估计效果良好,具有较好的鲁棒性。

图7 纵向车速估算对比

图8 横摆角速度估算对比
5 虚拟及实车验证
5.1 弯道避撞控制策略的虚拟验证
为验证弯道避撞控制策略的有效性,在PreScan软件中搭建弯道避撞场景,如图9所示。设置仿真工况为:前车在外车道上进行紧急制动,运行一段时间后停止,自车在外车道上匀速行驶,且内车道无车辆通过。

图9 弯道避撞场景建模
图10 所示为避撞过程中自车与前车的行驶轨迹曲线,仿真开始时,自车起始位置为外车道25 m处,前车在外车道57 m处。

图10 车辆行驶轨迹
仿真开始后,在25~56 m路段,自车一直在外侧车道匀速运动,同样在外侧行驶的前车突然紧急制动,自车通过传感器检测到与前方车辆的距离小于安全距离后,通过制动已经不能避免碰撞,自车采取换道操作进行避撞,并保持匀速行驶。从图中可以看出,自车行驶轨迹曲线在58~70 m路段的轨迹曲率发生明显变化,表明在此处进行了转向操作,换道至内侧车道。前车紧急制动行驶至X=66 m处停止,避撞过程中两条曲线没有交点,证明没有发生碰撞。
5.2 弯道避撞控制策略的实车验证
在外侧车道曲率半径为96 m、内侧车道曲率半径为81 m的沥青弯道路面进行测试,采用GPS采集车速、航向角、经纬度等信息,采用毫米波雷达采集距离信息。考虑实际行车过程中多数驾驶员的弯道行驶速度大于30 km/h,本文针对该情况进行弯道避撞的实车验证。设置前车最高车速30 km/h,自车最高车速为36 km/h。
试验过程中,传感器信号通过串口通讯发送至上位机,控制器计算出安全距离,若实际距离小于该值,采用弯道换道避撞控制算法,依据逆动力学模型计算出转向盘转角δ0,通过车身CAN发送转角信号,车辆接收到信号后进行换道,测试设备如图11所示。

图11 测试设备
将GPS采集到的经纬度点生成KML格式导入高清地图软件,其避撞路径如图12所示。

图12 两车的运动轨迹
其中A-B-C-D-E线段为自车的运动轨迹,F-G-HJ线段为前车(障碍车)的运动轨迹。自车在A点开始匀加速行驶,加速至36 km/h后到达B点,匀速行驶;自车在C点处检测到与前车的距离小于安全距离,开始转向换道,至D点完成换道操作,E点为自车避撞结束点。前车由F点开始加速,加速至30 km/h到达G点后匀速行驶,模拟前车在H点发生故障采取紧急制动,至J点停止。
试验过程中,自车从外侧车道换至内侧车道,避免了与前车的相撞,在低速避撞过程中自车无侧滑、甩尾等不稳定的情况,满足车辆行驶的稳定性要求。
6 结束语
本文提出一种在自车通过制动无法完成弯道避撞时的换道避撞算法。设计了基于斜坡正弦函数的避撞换道路径,利用弯道安全距离模型实时判断自车是否采取换道转向避撞措施,换道避撞过程中采用扩展卡尔曼滤波算法对车辆横摆角速度等关键状态变量进行实时跟踪,以保证弯道避撞的稳定性。仿真和实车验证结果表明,车辆在弯道行驶中通过换道有效避开了前方紧急制动的障碍车辆。

