基于改进UKF的自动泊车车辆位姿估计算法研究＊

谢有浩 赵林峰 张锐陈 张澄宇 辛鑫

（1.滁州学院，滁州239000；2.安徽猎豹汽车有限公司，滁州 239064；3.合肥工业大学，合肥 230009）

主题词：自动泊车 位姿估计 改进UKF滤波算法 常值噪声统计估计器

1 前言

自动泊车系统（Automatic Parking System，APS）是智能驾驶系统的典型功能，通过传感器获得轮速等信号并与算法相结合预测泊车过程中车辆的位姿状态，对于构建完整可靠的自动泊车系统有一定的应用价值。

文献[1]～文献[3]分别搭建了低速行驶工况下泊车系统坐标方程和低速倒车工况车辆运动学模型，并提出了自动泊车的路径规划及跟踪策略，但并未涉及对车辆位姿估计的研究。文献[4]～文献[6]搭建扩展卡尔曼滤波（Extended Kalman Filter，EKF）算法框架对泊车过程中的车辆位姿进行估计。EKF算法将非线性方程近似为线性方程再对目标进行卡尔曼滤波处理，得到的预测结果与实际状态必然存在较大差异。为克服EKF的局限性，一些学者提出了无迹卡尔曼滤波（Unscented Kalman Filter，UKF）算法。UKF算法的核心思想是采用无迹变换对非线性系统状态的后验概率密度函数进行近似。与EKF相比，UKF以二阶以上精度近似高斯非线性系统状态的后验均值与方差，具有实现简单、滤波精度高以及收敛性好等优点。为进一步提高UKF的滤波精度，文献[7]提出了一种可以自适应调整各Sigma点比重的比例因子，通过采用比例最小偏差采样提高UKF的计算精度。文献[8]分析了蒙特卡洛采样策略并验证了该方法具有一定的精确性，但前提是采样数量足够多。文献[9]和文献[10]研究表明，联邦卡尔曼滤波算法具有与集中滤波器相当的精度，且容错性能更好。上述文献在位姿估计过程中均假设系统噪声为均值为零的常值白噪声，但噪声实际往往处于先验统计未知的状态。

本文首先基于阿克曼转向几何建立泊车过程中的车辆运动模型，并建立观测方程，随后搭建常值噪声统计估计器，选用合适采样策略构造自适应UKF算法，最后通过联邦滤波结构求得下一时刻位姿状态预测值及协方差矩阵。利用MATLAB/Simulink软件进行仿真验证，并在基于CarSim整车模型和LabVIEW数据采集处理的试验台进行了硬件在环试验，验证了算法的有效性。

2 车辆运动学模型的建立

阿克曼理论的前提为假设汽车在转向过程中所有车轮均为滚动状态，此时车辆不受侧向力作用，所有车轮转向轴线交于一点，整车可以视为一个刚体。

由于车辆泊车过程中需要保持恒定低车速，可假设车辆运动不受侧向力作用，车轮没有发生滑移，因此可以基于阿克曼转向原理建立运动学模型进行研究。

图 1 所示为泊车运动学模型示意，其中，（xf,yf）、（xr,yr）分别为前、后轴中心点的坐标，（xr1,yr1）、（xr2,yr2）分别为左、右后轮中心点的坐标，v、vr分别为前、后轴中心点的速度，θ为车辆中心对称线与x轴方向的夹角，即车辆的偏航角，l为车辆轴距，ϕ为前轮转角。

图1 车辆运动学模型示意

后轮轨迹在车辆横向上的速度为0，可得：

由图1可知，前、后轴中心点坐标的关系为：

对式（2）求导，可得其速度关系为：

将式（3）代入式（1）可得：

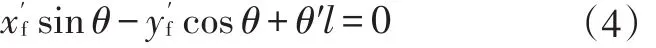
前轴中心点在x、y方向上的速度分别为：

将式（5）代入式（4），即可求得车辆回转圆角速度为：

将上述两式代入式（3）中，即可求得vr在x、y方向上的分速度：

将式（7）积分可得后轴中心点运动轨迹方程为：

3 改进UKF滤波器的搭建

根据车辆前、后轮分别搭载的两组编码器采集的信号建立两组不同的测量方程，从而分别构造两种滤波算法。联邦滤波[11]作为一种分布式的两级滤波结构，由1个主滤波器和若干子滤波器构成，可融合子滤波器的估计结果，得出精度更高、可靠性更强的泊车位姿估计结果。

考虑到泊车过程中车辆运动模型的状态方程和观测方程均含有非线性这一特点，且系统中含有先验统计未知的噪声，假设均为常值噪声，故采用加入常值噪声统计估计器的改进UKF算法分别实现联邦滤波结构中两个子滤波器的位姿估计结果。

根据图1，将非线性汽车系统状态向量定义为X=（xr,yr,θ,ω,vr）T，其中，ω 为横摆角速度，将观测向量定义为 Z=（ω,vr）T。

非线性离散系统模型为：

式中，Xk+1与Zk分别为系统的5维状态向量和2维量测向量；Wk和Vk分别为状态噪声和测量噪声；fk（）和hk（）分别为系统非线性状态函数和量测函数。

3.1 子滤波器的设计

通过安装在车轮上的编码器采集轮速信号，并由此得到车速，同时，由转向盘转角传感器采集得到转向盘转角φ。由此，可建立子滤波器n（n=1,2）的测量方程：

其中，观测变量为：

式中，ωn,k和vn,k分别为子滤波器i观测到的横摆角速度和后轴中心点速度；s=f,r分别表示前、后车轮；当n=1时，s=r，τ1=τ2=0；当 n=2 时，s=f，τ1=δ1,τ2=δ2；vs1,k、vs2,k分别为前轮或后轮左、右编码器采集得到的轮速信号计算所得车速；f（φ）为后轴中点转弯半径，是车辆转向盘转角φ的离散函数；δ1、δ2分别为左、右前轮转角；e为后轴中心点至车轮的距离；R1、R2分别为左、右后轮转弯半径。

f（φ）通过试验标定的方法确定，试验简要过程如下：采集转向盘转角和该转角下车辆后轴中点的转弯半径，然后得出离散数据表，实际应用中对其进行插值便可获得后轴中点的转弯半径。

子系统1、2的状态方程为：

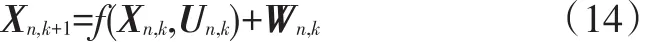
由式（7）和式（8）可得状态方程为：

式中，a1=cotφsinφsin（t）+T0cos（θk）；控制变量 Un,k=（0,l cotφ,ϕ,0,0,0）T；T0为采样时间步长；θk为k时刻车辆中轴线指向车头的方向与x轴的夹角。

3.2 子滤波器常值噪声统计估计器的设计

在自动泊车过程中，对于车辆位姿的估计不同于传统UKF滤波过程，滤波过程中的状态噪声和测量噪声处于先验统计未知状态，均值均不为零，因此假设系统噪声为常值噪声，需设计常值噪声估计器，对其进行估计。

基于上述分析，对传统UKF算法进行改进。首先提出2个假设[12]：

a.Wk和Vk为互不相关的高斯白噪声，且具有如下常值统计特性：

b. 初始状态X0与Wk、Vk互不相关，且服从正态分布，其均值和协方差矩阵为：

根据文献[12]中的定理一、定理二可以得出次优无偏MAP常值噪声统计估计器q̂k、Q̂k、r̂k、R̂k。

3.3 子系统局部位姿估计过程

分别获得状态方程和观测方程后，通过UKF算法对泊车过程中的车辆进行位置和航向更新。

3.3.1 初始化

车辆位置与航向的状态初值及误差方差矩阵初值分别为：

3.3.2 计算Sigma点

蒙特卡洛采样策略是一种随机性采样方法，得到的Sigma点集符合输入状态分布特征，利用蒙特卡洛算法得出大量Sigma点逼近概率密度分布，从而得到更高阶近似，以体现非线性函数本身的非线性。而当Sigma点数不超过500时，采用蒙特卡洛策略的UKF方法容易失效[13-14]，因此本文采用传统确定性采样方法和蒙特卡洛采样策略相结合的方法采集Sigma点。当采集的Sigma点数i≤500时，采用对称采样策略。对于均值为-X，方差为D-X的n维随机变量，产生一个矩阵χ，该矩阵由（2n+1）个列向量组成，表达式为：

式中，L=5为车辆状态向量维数；λ=（α2-1）L为控制形成Sigma点散布程度的参数；α为比例缩放因子（正值），取值范围为1×10-4≤α≤1，通常取较小的值。

当i＞500时，采用蒙特卡洛采样策略生成Sigma点，其步骤为：建立满足均值为-X，方差为D-X的高斯分布概率模型；对概率模型进行随机抽样；由抽样结果组成Sigma点集。

随后，直接调用MATLAB软件产生normrnd函数（A=normrnd（ave,sig,m）），返回m个均值为ave，标准差为sig的高斯分布的随机数A。采用蒙特卡洛采样策略，对均值为-Xk、方差为D-Xk的n维随机变量X，生成的m个Sigma点集为：

式中，（Xk）i为X 的第i个元素为D第i个对角线元素的平方根值。

3.3.3 时间更新

用Sigma点集矩阵代替状态方程中的X，得到新的状态方程：

式中，χ*i,k+1|k为车辆位置和航向的状态预测值。

对（2L+1）个状态预测值进行加权求和，可得到车辆位置和航向的状态预测值为：

同时，可计算得到车辆位置和航向状态方差为：

式中，Qk+1为（k+1）时刻车辆位置和航向状态方程的噪声方差矩阵；Pk+1|k为状态估计方差矩阵。

用式（25）得到的车辆位置和航向的状态预测值代替式（10）中的Xi,k，得到新的观测方程：

同时可计算得到车辆位置和航向观测方差为：

式中，Rk+1为（k+1）时刻车辆位置和航向观测方程的噪声方差矩阵。

车辆定位过程中统计特性权系数为：

3.3.4 测量更新

在时间更新后，继续对系统进行测量更新。利用车辆位置和航向状态值以及观测值，计算车辆位置和航向状态值和观测值的协方差：

结果输出：

因此-可得（k+1）时刻汽车位置和航向，及其误差方差矩阵Xk+1=[]，扩展到任意时刻，得到车辆UKF子滤波器的定位轨迹。

3.4 自适应UKF算法流程

根据所搭建的常值噪声统计估计器以及UKF过程可以得到自适应UKF计算过程：

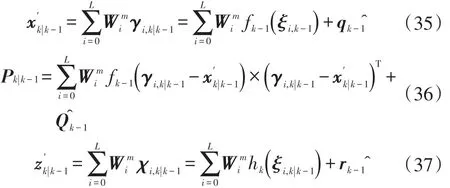
3.5 主滤波器的设计

联邦滤波器具有多种结构形式，从信息反馈的角度可分为无反馈结构（NR）和有反馈结构（FR）两种。无反馈结构的优点在于信息传递更及时，且具有一定的容错能力；有反馈结构具有更强的鲁棒性，精度相比于无反馈结构更高。本文搭建两种结构形式并进行比较分析，流程框图分别如图2、图3所示。联邦滤波器中，主滤波器的作用在于对来自子滤波器的局部估计结果进行信息整合，将k时刻2个子滤波器的局部估计值X1、X2及其估计误差的协方差矩阵P1、P2进行融合，并最终得到全局融合估计结果，即状态的预测结果Xg及其协方差Pg。

图2 无反馈结构的流程框图

图3 有反馈结构的流程框图

无反馈结构的表达式为：

有反馈结构在无反馈结构基础上对全局融合估计结果进行信息分配，并反馈给各子滤波器用于下一工作循环的局部估计值。因此，有反馈结构更复杂的同时，精度也有所提高。有反馈结构表达式为：

式中，β1和β2为信息分配系数。

根据式（38）～（40），计算两种主滤波器结构得出的最后预测值。

4 仿真验证

为了验证本文所设计的自适应UKF算法对泊车过程中车辆位姿的估计效果，对其进行仿真验证。仿真车辆的相关参数如表1所示。

表1 自车相关参数

其次构建基于联邦-无损卡尔曼滤波器的位姿估计算法模块。它接收CarSim车辆运动学模型的“虚拟”传感器信号，包括车轮轮速信号和转向盘转角等，进而算出车辆的位姿信息估计值。仿真时，人为地为轮速信号添加噪声，模拟实际传感器中信号噪声的干扰。同时，CarSim车辆模型也能实时地输出车辆的位姿信息作为参考值。将参考值与估计值进行对比，便可对算法进行评估。仿真流程如图4所示，本次仿真另外加入标准UKF与EKF算法进行对比，结果如图5、图6所示。

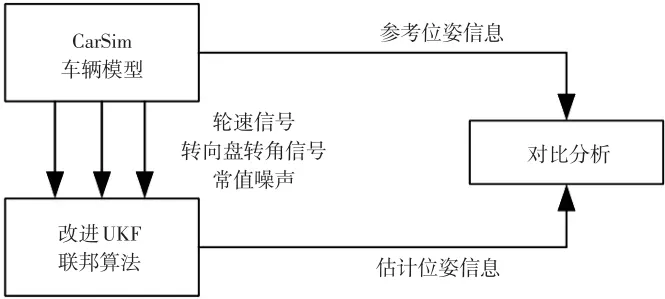
图4 仿真分析流程框图

图5 3种结构估计值横向偏差对比

图6 3种结构估计值纵向偏差对比

由图5可知，在X方向上，改进UKF算法、标准UKF算法、EKF算法所得到的估计值与理论值的偏差范围分别为[-1.13,2.97]cm、[-1.51,3.28]cm、[1.32,3.87]cm。改进UKF算法估计值与理论值偏差的绝对值均小于另外两种算法的偏差绝对值。

由图6可知，在Y方向上，改进UKF算法、标准UKF算法、EKF算法所得到的估计值与理论值的偏差范围分别为[0.40,4.45]cm、[1.04,5.33]cm、[1.81,5.63]cm，Y方向上3种结构的估计值均大于理想路径值。改进UKF算法估计值与理论值的偏差绝对值均小于另外两种算法的偏差绝对值。

综上，改进UKF算法估计车辆位姿的精度更高。

5 硬件在环验证

为了验证基于改进UKF算法设计的泊车位姿估计算法的有效性，采用CarSim汽车模型的仿真环境，进行硬件在环试验验证。根据某款车型的参数在CarSim中设置整车模型、汽车起始点位置、车速和泊车路面工况，并在计算机中实时运行；在LabVIEW中处理和显示各路传感器信号，由PXI主机执行；同时，利用数据采集卡和CAN通讯接口系统采集转向盘转角信号，并将信号实时发送给EPS控制器和PXI主机。试验平台主要设备包括：校企联合研发的APS控制板及EPS控制器、雷达控制器、转向管柱以及各类传感器等。为了真实模拟轮胎与地面的作用力矩，实现对阻力的真实模拟，台架还包括伺服电机组成的阻力模拟总成，通过CarSim输出齿条受力信息给伺服电机，由LabVIEW控制伺服电机输出力矩给齿轮齿条转向器。试验平台如图7所示。

图7 硬件在环试验平台

本文选用虚拟干燥路面进行试验，并将车速设为恒定3.6 km/h。启动自动泊车功能后，接口系统采集硬件系统中的传感器信号并处理之后实现与软件系统中运行的整车模型及控制器进行信息实时交换。

试验结果如图8所示：EKF算法估计路径与实际路径差异始终较大，在相同横坐标下，在Y方向上的最大偏差为21.9 cm；标准UKF算法估计结果也出现局部精度下降的情况，在相同横坐标下，在Y方向上的最大偏差为13.1 cm；改进UKF算法估计结果始终贴合实际路径，在相同横坐标下，在Y方向上的最大偏差为7.2 cm。

图8 位姿估计效果对比

综上，本文采用的改进UKF位姿估计算法具有更高的精度和更好的收敛性。

6 结束语

本文从估计泊车位姿的角度出发，在传统UKF方法的基础上添加常值噪声估计器，并采用精确度更高的综合性Sigma点集采样策略构成改进UKF算法。相比于传统位姿估计算法，该算法对UKF的稳定性没有影响，更适用于泊车过程中的车辆位姿估计，且不要求精确已知噪声的先验统计。利用传感器采集得出的信号作为观测变量，结合由阿克曼转向几何得出的运动学状态方程进行时间更新以及测量更新，搭建两种联邦卡尔曼滤波结构，由主滤波器输出估计的最优值。在MATLAB/Simulink软件中进行了仿真验证，并在基于CarSim整车模型和LabVIEW数据采集处理的试验台进行了硬件在环试验，验证了算法的有效性，为自动泊车系统实时估计预测车辆位姿提供支持，同时也增加了泊车过程的安全性与可控性。