钢管塔环型加肋空间节点抗弯性能分析
杨子烨, 邓洪洲
(同济大学 土木工程学院,上海 200092)
近年来,钢管塔在我国的大跨越线路工程以及同塔双(多)回线路中得到广泛应用[1].节点是钢管塔的重要部位,它的连接构造和承载力关乎整塔乃至整个线路工程的安全.与传统钢管焊接节点相比,插板节点具有受力和构造简单、焊接工作量小、工业化程度高以及现场施工方便等优点,因而很快为设计人员所接受,较多应用在实际工程中.为提高插板节点极限承载力,节点板端部多采用环型肋板(鞍型板、1/4环板、1/2环板和全环板)进行局部加强[2].其中,全环板多应用在塔中较为复杂的空间节点处,例如横担与塔身主(吊)材连接节点、双K型节点.
目前,插板节点的研究主要集中在平面节点极限承载力方面[3-7],对空间插板节点的研究较少.在国外,日本研究较早,形成了较为成熟的设计规范《输电线路钢管塔制作基准》(JSTA)[8],已有大量研究表明该规范公式具有较大安全裕度,简单套用日本规范方法并不可取.刘红军等[5]通过对单、双侧钢管节点受弯模型的试验研究和理论分析,提出了全环板加劲钢管节点极限承载力建议公式,该公式仅针对平面节点,未能考虑节点的空间效应;严立新等[6]通过对多组钢管节点进行试验研究和数值分析,提出了两种工况荷载作用下全环板钢管节点承载力建议公式,该建议公式本质上仍针对平面节点且未能考虑全环板和主管的变形耦合效应;刘堃等[7]通过对全环板KK型插板节点进行有限元分析,建立了全环板空间KK型节点的承载力建议公式,该公式虽然考虑了节点的空间性,但尚未得到试验验证,且计算较为繁琐.综上所述,急需对全环板空间钢管节点进行研究.
本文通过试验研究及有限元分析对两类空间节点(C90、C180)受弯性能进行研究,得到节点的破坏模式和抗弯承载力.其次,针对不同的破坏机理,通过塑性理论和有限元参数分析的方法,得到了几何尺寸和主管应力对承载力的影响.最后,通过理论推导及回归分析的方法提出了较为完整的环型加肋空间钢管节点的抗弯承载力建议公式.
1 试验设计
1.1 试验模型
如图1所示,共设计了节点板互呈90°(C90)和180°(C180)的两组试件,每组2个节点.

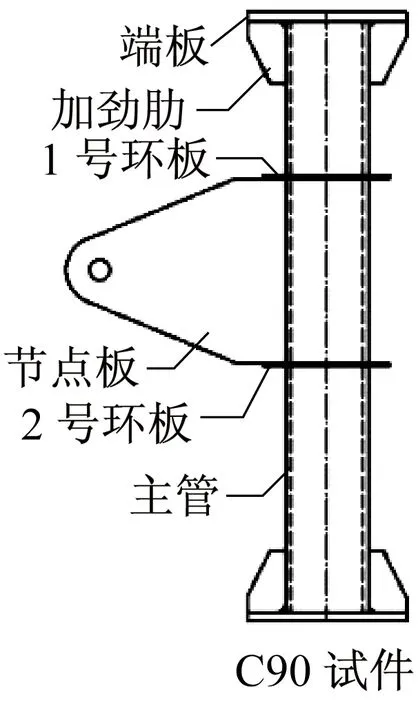
图1 环型加肋空间节点Fig.1 Multi-planar steel tube connection
节点均由主管、环板和节点板组成,且各部分节点规格尺寸完全相同.主管尺寸为Φ273 mm×6 mm,长度为2 m,环板高度R=70 mm,环板厚度tr=6 mm,节点板高度B=603 mm,节点板厚度T=22 mm,螺栓孔中心到管壁的距离H=608.5 mm.其中,主管和环板采用Q345钢材,为防止试验中节点板发生破坏,节点板采用强度更高的Q420钢材.此类节点中,环板常与主管共同作用,形成主管-环板模型,如图2中阴影部分所示.节点几何参数及主管-环板模型归一化参数如图2所示.
1.2 材性试验
空间节点共采用了Q345和Q420两种材料的3种不同截面规格,材性试验针对每种截面规格均制作了3件材性试验试件,并进行了室内室温材性拉伸试验[9],材性试验结果见表1.表中采用Q345-6p、Q345-6c和Q420-22p对材料进行编号,其中345和420为名义屈服强度,6和22为板件厚度,p表示节点板或环板,c表示主管.表中数据为每组3个试件材性试验结果的均值.

图2 T型截面剖面示意Fig.2 The profile of T section表1 材性试验结果Tab.1 Material test results

编号名义屈服强度/MPa试验值E/GPaΝfy/MPafu/MPafy/fuQ345-6p345207.000.260479.69531.360.90Q345-6c345206.910.264466.72519.560.89Q420-22p420216.700.273503.53632.900.80
1.3 荷载分解及等效
如图3所示,节点荷载主要包括主管轴力N和节点板作用力F.其中,节点板作用力对主管而言可简化为剪力Q和附加弯矩Ma,同时主管受到局部弯矩引起的水平力P的作用,MA为两节点板附加弯矩Ma之和.由于节点板剪力Q和附加弯矩Ma的影响,2号环板截面处主管作用力较1号环板截面处主管作用力大,即2号环板截面处在侧向外力P和主管合力作用下将首先产生较大的应力,最早破坏.对于C90节点,2号截面处主管除主管轴力和剪力外,附加弯矩相互叠加,引起主管内较大次应力;对于C180节点,附加弯矩方向相反,相互抵消,主管应力仅包括主管轴力和节点板作用力引起的正应力.除此之外,2号环板截面处主管受到水平力P的作用.在2号截面处的等效荷载可按照式(1)~式(6)进行计算.

a C90节点荷载分解
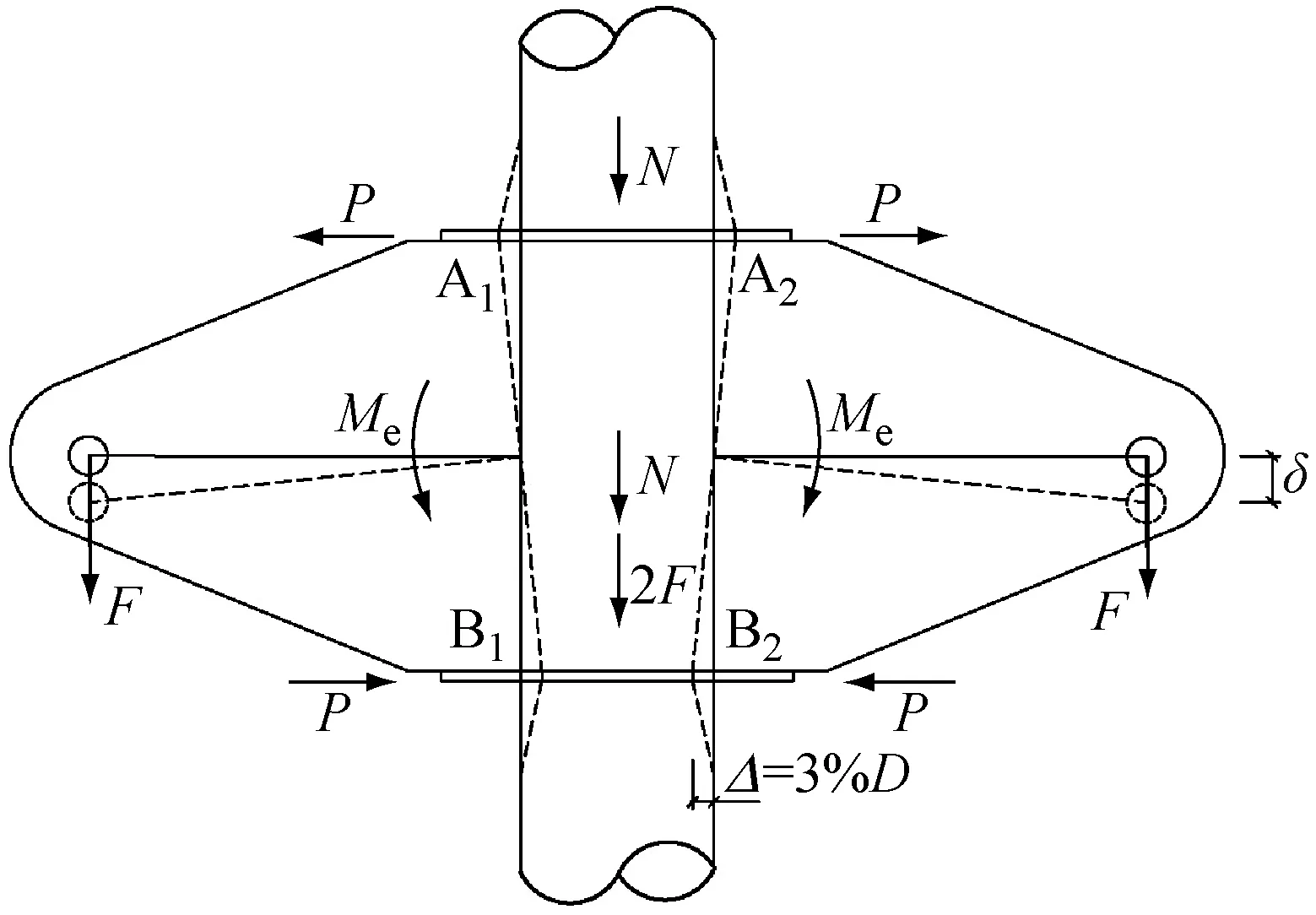
b C180节点荷载分解图3 节点荷载分解及等效荷载Fig.3 Load decomposition and equivalent load of connections
C90节点:
Ma=F(D+2H)/2
(1)
Q=2F
(2)
Me=PB
(3)
C180节点:
Ma=0
(4)
Q=2F
(5)
Me=PB
(6)
式中:Me为局部弯矩.
1.4 测点布置
节点试验的位移计及测点布置如图4所示图中A1、A2、B1、B2为节点板主管和全环板的交点.每个试件共布置5个位移计,其中3个位移计(D1、D2和D3)布置在上端板处,用来监测试验中的主管偏转和

a C90试件测点布置
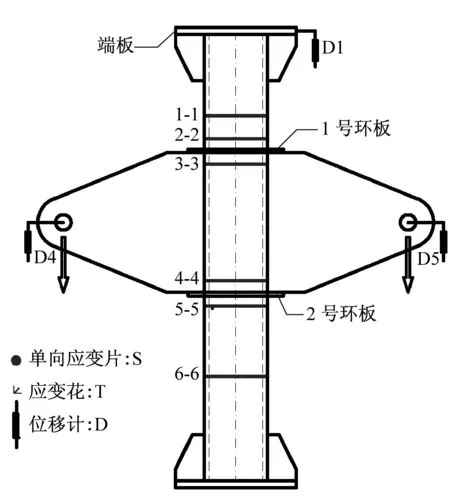

b C180试件测点布置图4 测点布置Fig.4 Arrangement of measuring points
纵向位移.其余两个位移计(D4和D5)用来测量节点板的竖向位移.沿主管共布置6个截面的测点,其中1-1截面和6-6截面用来监测主管的应力情况,2-2、3-3、4-4、5-5截面为主管应力集中区.环板上应力较为复杂,布置多组三向应变片进行测量.
本文所指的极限承载力为以下两种荷载值的较小值:①荷载-位移(P-Δ)曲线的极值点所对应的荷载值;②变形量Δ(见图3)达到主管直径3%时所对应的荷载值.
由于试验中直接测得的结果是作用在节点板上的荷载和荷载作用点的位移.同时,由于节点板刚度较大,其变形可以忽略[10].为便于应用,承载力和变形按式(7)~式(8)进行转换.
Me=PB+Mc=FH
(7)
δ=2HΔ/B
(8)
式中:P为作用到环板上的力;Mc为主管管壁提供的抗力弯矩,其数值一般较小,可以忽略;F为作用在节点板上的力;δ为F对应的节点板位移;Δ为P对应的管壁变形.
2 试验过程
2.1 试验加载
如图5所示,试验过程中,主管和节点板分别加载.

a C90试件试验加载b C180试件试验加载
图5试验安装加载
Fig.5Testset-up
主管加载通过大型试验机(C90)或2 000 kN千斤顶(C180)来完成.节点板加载受到加载仪器数量的限制,专门设计了两套具有足够刚度,且传力可靠的拉-压转换装置,见图5a.通过该装置可将1 000 kN千斤顶的压力转换为相同大小的拉力.为保证节点板同步加载,两个千斤顶由同一套油泵系统驱动.为防止试验过程中,节点由于不平衡力矩而发生转动,上端板顶部安装了加载头和横向反力梁.试件底部安装在球铰支座上.
试验采用单向分级加载.次序为主管荷载和节点板荷载同步等比例加载至预先设定的荷载值,如表2所示,随后主管上千斤顶(试验机)保持预定等级不变,节点板上千斤顶继续施加荷载至1.5倍预定荷载值后,继续缓慢施加荷载直至节点出现明显塑性变形.每级荷载分为10个加载步,每个加载步完成后停约3 min,待应变片数值稳定在一定范围,施加下一级荷载.

表2 预定荷载值Tab.2 The value of the predetermined loads
注:主管荷载取0.1Npl,Npl=fyA,A为主管截面面积,节点板荷载为JSTA规范设计值,规范中不包括C90节点设计公式,其节点板预定值通过平面节点公式得到.
2.2 试验现象描述
通过分析测点数据可知,对于C90节点,当荷载较小时,各测点应变随荷载增加线性增加,节点板下方5-5截面测点应变明显大于其他测点.如图6a所示,当荷载达到预定值1.03倍时,两节点板引起的塑性应变相互叠加,节点板受压端主管(S15测点)首先出现屈服,随后塑性范围逐步扩展,S14和S16测点先后进入塑性状态,此时,2号环板上的测点仍处于弹性状态.随荷载进一步增加,管壁塑性区域相互贯通,主管出现较大塑性变形,节点不能继续承载而达到极限状态,最终破坏形式表现为C90节点下端钢管出现明显鼓出而破坏.根据节点承载力判断准则,C90节点承载力为荷载-位移曲线极大值,分别为285.42 kN和297.53 kN.
对于C180节点,节点荷载加至1.26倍预定荷载时,2号环板上测点(T4、T5、T7、T8)首先出现屈服状态,测点应变随荷载增加呈现非线性增加趋势,如图6b所示.随着节点板荷载不断增加,环板测点应变增加较快,环板塑性区域不断扩展,同时主管测点也达到屈服应变.当节点荷载加至2.06倍预定荷载值时,千斤顶无法继续加载,传感器数值出现较为明显的波动,位移计增加较快.此时,钢管和环板塑性区域贯通,2号环板及主管出现明显的横向塑性变形.根据节点承载力判断准则,C180节点承载力为荷载-位移曲线δ=16.54 mm时的荷载值,分别为277.71 kN和292.71 kN.
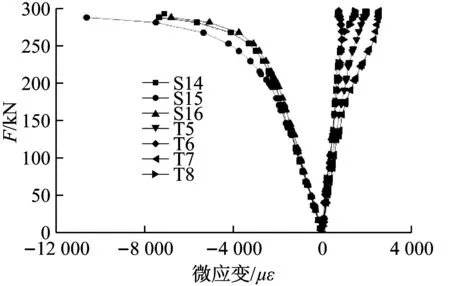
a C90节点
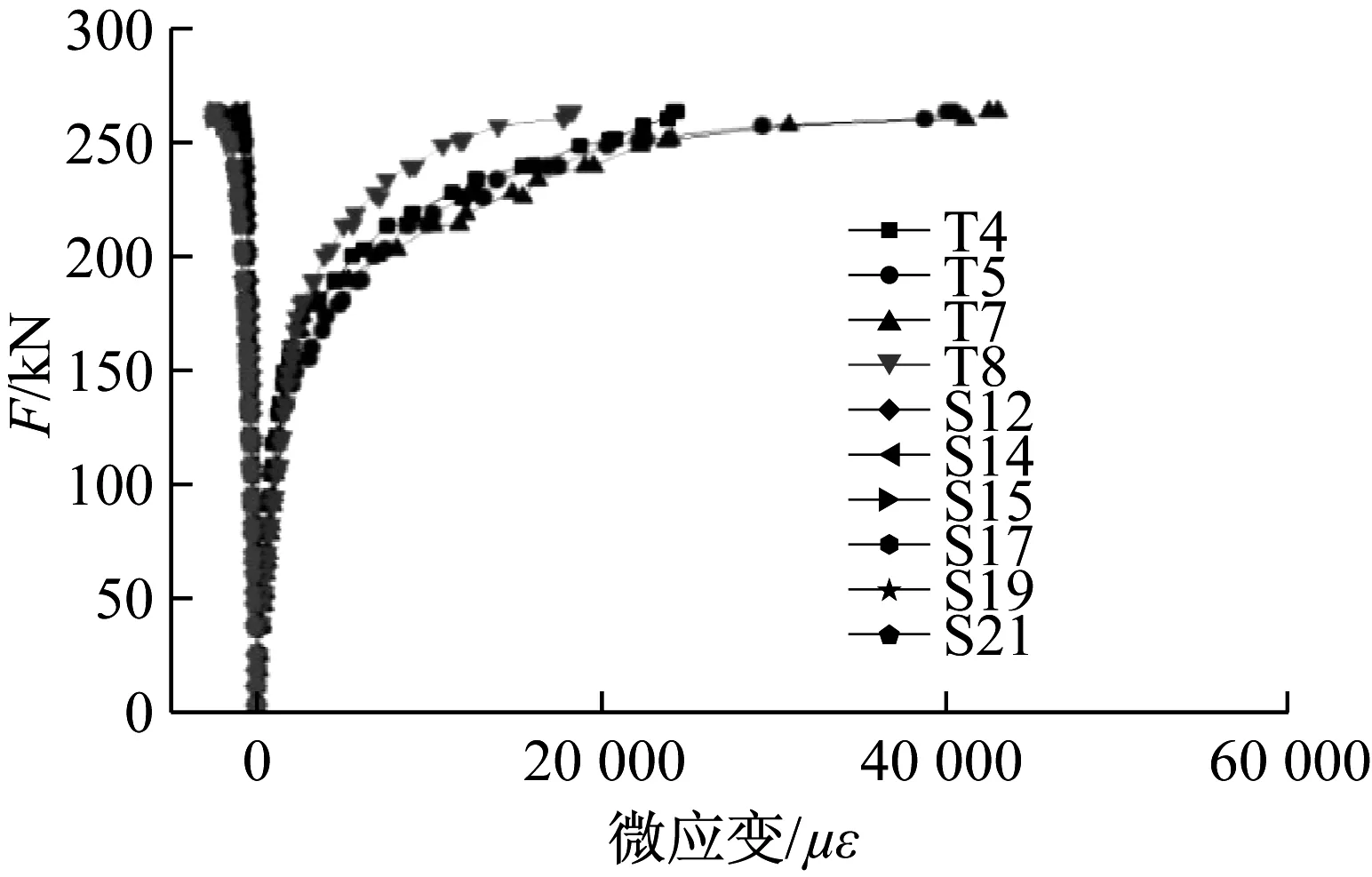
b C180节点图6 荷载-应变曲线Fig.6 Load-strain response curves
2.3 试验主要结果讨论
对于环型加肋空间节点,2号环板截面处主管作用力较大,节点承载力由2号环板及其周围主管控制.C90节点在附加弯矩的作用下,主管内产生较大次应力,使得节点在2号环板截面处发生主管局部屈曲破坏.这种破坏模式与主管的截面尺寸及材料强度有关.C180节点在水平力作用下,2号环板及附近主管产生较大横向塑性变形.在这种破坏模式下,环板与主管共同变形,构成了环板-主管模型,即由T型截面构成的环梁.节点的抗弯性能由环板-主管模型的横向承载力(P)控制.造成不同破坏模式的主要原因是:节点板夹角较小时(θ=90°),主管内应力分布不均匀使得主管局部屈曲先于环板-主管模型横向塑性变形出现,节点板夹角较大时(θ=180°),主管内应力较为均匀,环板-主管模型横向塑性变形先于主管局部屈曲出现.因此,在后续分析中,针对节点的两种破坏模式及破坏机理,分别提出计算方法.对于主管局部屈曲破坏,采用对主管最不利截面进行塑性强度验算的方法.对于环板-主管模型塑性变形,采用计算环板-主管模型水平承载力的方法.
3 有限元分析
3.1 有限元建模
借助有限元软件Ansys15.0[11]对节点进行有限元计算.节点模型采用Solid185单元进行建模,见图7,并采用MPC184刚性梁单元建立主管端部和加载孔的刚性面,考虑到主管端部对结果的影响,同时对节点端板及端部肋板进行建模.除对试验节点进行有限元建模外,为研究环板的加劲效应,对相同尺寸的无环板节点进行建模.钢材的本构关系根据材性试验结果采用多线性随动强化模型,如图8所示.边界条件按试验情况选取,主管下端板为球铰支座,约束三个方向的平动位移,上端板约束垂直于主管轴线方向的两个平动位移,节点板加载孔约束节点板面外位移.加载过程与试验单调分级加载情况相同.

图7 有限元模型Fig.7 The finite-element model
图8 材料的应力-应变关系模型Fig.8 The stress-strain curve
3.2 有限元模型的验证
如图9所示,有限元分析所得两类节点破坏模式与试验结果基本相同,即C90节点为2号环板下侧主管局部屈曲破坏,C180节点为2号环板-主管模型产生较大横向塑性变形而破坏.
两类节点荷载-位移曲线如图10所示,横坐标为位移计D4和D5所测数值,纵坐标为节点板荷载.试验中,C180-1试件中位移计D4出现明显波动,记录结果未显示在图中.有限元荷载-位移曲线初始斜率、极限荷载较试验结果偏大,这主要是由于有限元模型较为理想化,未能考虑实际中存在的节点初始缺陷、加载偏心、残余应力等因素.从荷载-位移曲线的整体趋势来看,有限元结果与试验得到的结果较为吻合,两类节点承载力试验值与计算值之比的均值分别为1.088和1.045,表明有限元结果真实可靠.图10同时将试验节点有限元模型与无环板有限元节点模型(FEw)的荷载-位移曲线进行对比,试验节点承载力约为相应的无环板节点的3倍,表明环板能有效提高节点的承载力.


a C90试件破坏模式


b C180试件破坏模式图9 节点试件破坏模式Fig.9 Connection failure modes

a C90试件

b C180试件图10 荷载-位移曲线Fig.10 The load-displacement curves
3.3 计算参数的选取
针对2号环板处主管横向塑性变形破坏,2号环板-主管模型的受力模式如图11所示.为考察几何参数对环板-主管模型水平承载力的影响,对节点进行有限元参数分析,节点归一化参数见表3.环板-主管模型的荷载-位移曲线,应在节点有限元计算后,提取节点板与环板相交截面的节点内力作为横向荷载P.P所对应的位移为三板(节点板、环板、主管)交汇点(B1、B2点)的水平位移.得到荷载-位移曲线后,按照节点极限承载力判断准则得到环板-主管模型的承载力Pu2.

C90

C180图11 环板-主管模型受力示意图Fig.11 The force conditions of annular ribbed plate-to-chord model表3 节点参数分析几何尺寸Tab.3 Geometric parameters for parametric analysis
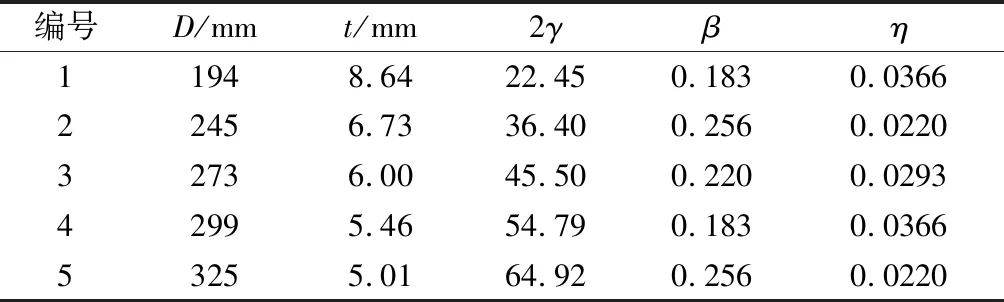
编号D/mmt/mm2γβη11948.6422.450.1830.036622456.7336.400.2560.022032736.0045.500.2200.029342995.4654.790.1830.036653255.0164.920.2560.0220
注:表中D为钢管塔主材常用尺寸;t遵循主管截面面积与Φ273×6面积相等的原则计算得到;β(β=R/D)、η(η=tr/D)为可变参数,即在参数分析中,对于每种主管截面环板归一化尺寸(β、η)为单一变量.
3.4 计算公式数学模型
对于2号环板处主管横向塑性变形破坏模式,环板-主管模型与CIDECT[12]规范中横插板-主管模型的受力情况和几何形状相似.因此,可以借鉴CIDECT规范中公式为回归分析的数学模型.对于折减系数Qf,可将该公式中常系数替换为回归系数,并将替换后的式子作为Qf非线性拟合的数学模型[13].由于环板-主管模型几何参数与横插板-主管模型不同,不能简单的将Qu中系数替换,但仍仿照规范公式将Qu表达成几个多项式相乘的形式,每个多项式包含一个归一化几何参数.回归分析数学模型表达式见式(9)~式(11).
Pu2=QuQffyt2
(9)
Qf=(1-|n|A1)B1
(10)
Qu=f1(2γ)f2(β)f3(η)
(11)
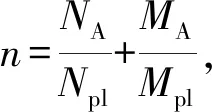
3.5 主管轴向应力对承载力的影响
以C180试件中2号环板-主管模型为研究对象,研究主管应力比对环板-主管模型横向承载力的折减效应.主管轴力设为变量,分别计算N=(-0.95, -0.9, -0.8, -0.6, -0.4, 0, 0.4, 0.6, 0.8, 0.9, 0.95)Npl时的承载力.如图12所示,纵坐标为折减系数(Qf=Pu2/Pu2(n=0)),横坐标主管应力比中计入附加弯矩及节点板剪力的影响,因此数据整体向受压方向(n<0)偏移.从数据点可以看出,承载力随主管应力比增加而降低,且随主管应力比增加其降低程度相应增加.当|n|=0.9时,折减系数下降35%左右,当|n|>0.9时,数据点离散性增加且折减系数急剧降低,当|n|=1时,折减系数为0.这是由于当主管接近屈服强度时,其抗水平力P的能力大大下降.因此,从工程安全和经济的角度考虑,建议|n|<0.9.
对于主管局部屈曲破坏,可以通过主管应力比对主管最不利截面进行验算,验算标准为|n|<1.据此验算标准与节点荷载分解及等效公式推导得到节点的最大弯矩.
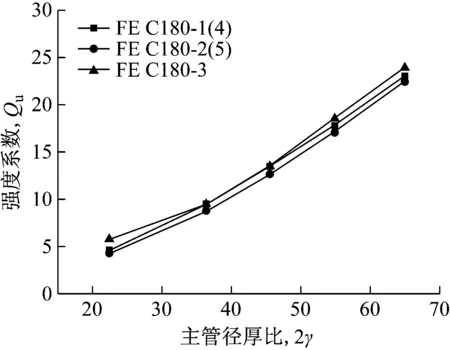
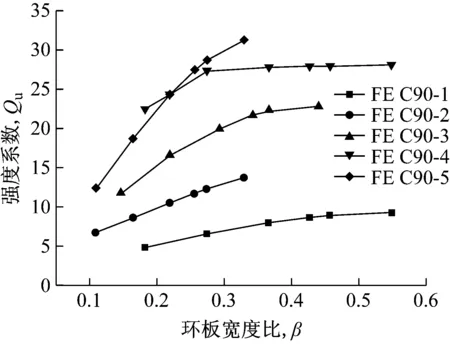
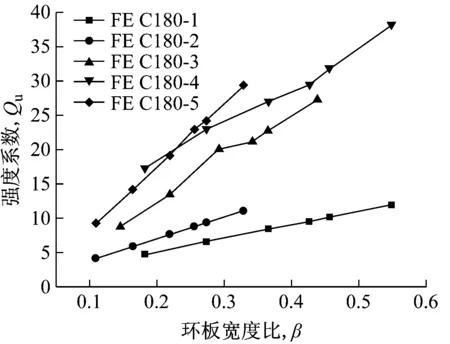
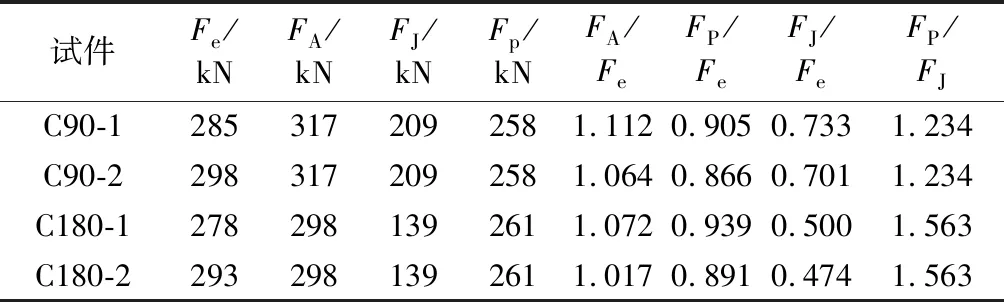
如图12所示,JSTA规范公式的折减系数Kn(仅包括主管受压情况,n<0)与有限元计算结果进行对比.结果表明:当主管应力比较小时(-0.4 图12 主管应力比n对折减系数Qf的影响Fig.12 The influence of chord stress ratio n on the reduction coefficient Qf 在计算几何参数对强度系数影响时,不计入主管应力对环板-主管模型横向承载力P的降低效应,即折减系数设为Qf=1.如图13~图15所示,纵坐标为强度系数Qu=Pu2/fyt2,横坐标为归一化的几何参数.强度系数随主管径厚比增加呈二次曲线形式增加,Qu与2γ之间的相关性可用一元二次函数来表达,见式(12). a 2γ对Qu的影响(C90) b 2γ对Qu的影响(C180)图13 主管径厚比2γ对强度系数Qu的影响 Fig.13Theinfluenceofchorddiameter-to-thicknessratio2γonthepartialdesignstrengthfunctionQu 对于C90节点,当β和η较小时,强度系数随环板参数增加呈线性增加趋势,当β或η达到较大数值时,Qu随参数增加的幅度减小,呈现明显的非线性关系.这是由于当环板几何参数足够大时,破坏模式由环板-主管模型的塑性横向变形破坏模式转为主管局部屈曲破坏模式.对于C180节点,强度系数与环板几何参数之间呈明显的线性关系.因此,对于环板-主管模型塑性横向变形破坏而言,Qu与η和β之间的关系可用式(13)~式(14)表示. f1(2γ)=A2(2γ)2+B2(2γ)+C2 (12) f2(β)=D2β+E2 (13) f3(η)=F2η+G2 (14) 式中,A2、B2、C2、D2、E2、F2和G2均为回归参数. a β对Qu的影响(C90) b β对Qu的影响(C180)图14 环板宽度比β对强度系数Qu的影响 Fig.14Theinfluenceofannularribbedplatewidth-to-chorddiameterβonthepartialdesignstrengthfunctionQu 结合大量有限元计算结果,利用最小二乘法进行回归分析,拟合得到环型加肋空间节点的极限弯矩计算如下: Mmax=min(Pu1,Pu2)B C90试件: (1)Pu1的计算 (2)Pu2的计算 Pu2=QuQffyt2 Qu=2.47(0.154γ-1)(2.409β+1)(24.705η-1) C180试件: (1)Pu1的计算 (2)Pu2的计算 Pu2=QuQffyt2 Qu=0.592(0.175γ-1)(8.883β+1) (57.223η-1) 式中:Qf=(1-|n|1.7)0.22(n<0),Qf=(1-|n|2)0.25(n>0),Npl=fyA,Mpl=fy(D3-(D-2t)3)/6. b η对Qu的影响(C180)图15 环板厚度比η对强度系数Qu的影响 Fig.15Theinfluenceofannularribbedplatethickness-to-chorddiameterηonthepartialdesignstrengthfunctionQu 不同方法和公式得到的节点承载力见表4.利用本文建议公式得到的承载力与试验值较为接近且小于1,表明建议公式能较好地反映节点的承载力且留有一定的安全裕度.JSTA规范公式计算结果约为试验结果的0.7倍(C90)和0.5倍(C180),表明JSTA规范过于保守. 表4 空间环形加肋钢管节点抗弯性能计算结果对比Tab.4 Results comparison of ultimate bearing capacity of multi-planar steel tubular connection 注:表中采用节点板作用力F表示节点的抗弯性能;Fe为节点试验承载力;FA为经过有限元分析得到的承载力;FJ为按JSTA规范计算得到的承载力;C90节点承载力按其平面节点公式计算得到;Fp为根据本文建议公式计算得到的承载力. 本文通过试验研究和有限元分析,探讨了环形加肋空间节点的抗弯性能、失效模式及其影响因素,并提出了承载力建议公式.本文主要结论如下: (1) 环板加肋钢管节点的破坏模式分为主管局部屈曲和环板-主管模型横向塑性变形.节点破坏模式与主管应力相关.当节点板间夹角较小,弯矩相互叠加,主管中出现较大次应力,引起主管局部屈曲破坏.当节点板间夹角较大,主管内应力较小,受水平力作用出现横向塑性变形破坏. (2) 外加环板能有效提高节点承载力,对于文中环板尺寸,有环板节点承载力约为相同尺寸无环板节点承载力的3倍. (3) 本文对JSTA规范公式的准确性进行了考察.当n>-0.4时,JSTA规范折减系数Kn偏于不安全,当n<-0.4时,Kn偏于保守.JSTA规范计算的节点承载力过于保守,约为C90节点试验值的0.7倍,为C180节点试验值的0.5倍. (4) 针对不同的破坏模式提出了较为完整的环型加肋空间钢管节点承载力建议公式.建议公式计算结果与试验结果进行了对比.结果表明,建议公式可靠有效,能较好地预测节点的抗弯承载力.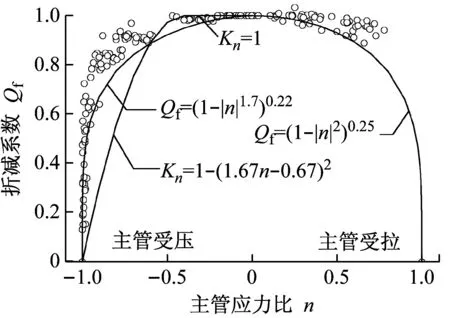
3.6 几何参数对承载力的影响

4 建议公式
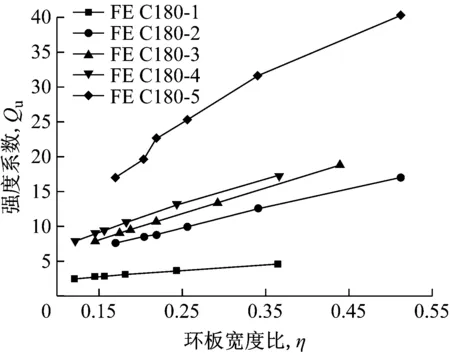
5 结论

