基于旅行时间分析的城轨乘客路径集验证方法
朱 炜, 韦 锦, 洪 玲, 徐瑞华
(1. 同济大学 道路与交通工程教育部重点实验室, 上海 201804;2. 同济大学 上海市轨道交通结构耐久与系统安全重点实验室, 上海 201804)
客流是城市轨道交通网络化运营管理的基础,科学计算和分析客流在网络上的分布情况是解决票款清分清算、网络运营协调、列车运行图编制、运营风险控制,以及突发事件应急处置等一系列重要问题的前提和依据.然而,复杂连接的轨道交通路网结构以及与此相应的“一票换乘”体系,使得乘客在网络上的出行情况无法被直接确定,是运营管理部门进行网络客流分布计算及分析的主要困难.
现阶段,国内城市轨道交通系统广泛采用一类基于多路径的出行路径选择估计模型,该模型考虑OD间K短路径的搜索,对其合理性进行判断并生成有效路径集,而后在有效路径中进行路径选择估计,包含了有效路径集生成和路径选择估计两部分.其中,生成的有效路径集是否合理是后续路径选择估计的前提与基础,以往研究大多侧重后者[1-3]而对前者未有足够的重视,且主要采用基于人工客流调查的方式[4-6].但随着城市轨道交通系统在网络规模、复杂程度及时空差异不断加大的情况下,生成的有效路径与实际情况不甚吻合的情况时有发生.事实上,北京、上海等地的城市轨道交通运营管理部门在实现了大规模网络客流分布计算的基础上,已开始注意到有效路径集合理性对乘客路径选择估计及网络客流分布计算结果的影响,并开始着手进行有关的路径集验证工作[7-8],但所用的方法仍主要借助于客流调查,通过调查员“跟踪”、“模拟”等方式获取选定OD间的乘客实际出行路径情况,应用实施成本巨大且有较大的随机性和片面性.
另一方面,伴随交通领域科技水平的提高,国内城市均实现了乘客通过各类支付方式(包括公交卡、地铁卡和移动支付等)进出轨道交通系统、享受相应出行服务.这些票卡保存着海量的历史数据,并且在诸如自动售检票系统(AFC)、列车自动监控系统(ATS)等城市轨道交通特有的运营管理与软硬件技术条件下可以得到更为丰富的乘客出行信息[8],特别是带旅行时间信息的OD数据等,从而为数据驱动的城市轨道交通网络乘客出行路径集验证提供了可能.
由此,本文从分析现有路径集生成算法出发,基于AFC刷卡记录中提取的OD旅行时间数据,引入大数据快速聚类分析算法,提出数据驱动的有效路径集验证方法,以满足当前对城市轨道交通网络客流分布的精细化、智能化分析要求.
1 现有客流分布模型路径集问题分析
一方面,基于城轨交通出行路径选择特性可知,乘客一般选择时间较短的路线;另一方面,由于网络的复杂性使得最短路判断可能出现差异,乘客个体选择行为又带有一定的随机性.因此,国内网络化运营条件下的城市轨道交通系统采用一类基于K短路径搜索的有效路径集生成算法,其主体算法流程步骤如下:
(1)K短路径搜索.基于城市轨道交通物理网络拓扑,通过K短路算法得到网络中任一OD间K条(K的取值可以根据需要设置,一般从计算时效性考虑取K≤5)不包含重复节点的渐短路径.
(2) 路径有效性判断.通过路径搜索算法得到的K条渐短路径中,一些不合理的路径可以认为乘客不会选择.以出行阻抗的容许区域来判断某一路径是否合理,得到网络中任一OD间有效路径集,其判断公式可以表示为(不同城市之间稍有差异)
Tw,max=min(Tw,min(1+θ),Tw,min+U)
(1)
Tw,range=min(Tw,min×θ,U)
(2)
式中:Tw,max为有效路径出行阻抗值的上界;Tw,min为最短路径的出行阻抗值;Tw,range为有效路径超过最短路径出行阻抗值的最大容许值;θ是相对阈值系数,为Tw,range与Tw,min的比值,表示有效路径可以超过最短路径出行阻抗值的最大相对比值;U是绝对阈值,为Tw,max与Tw,min的差值,表示有效路径可以超过最短路径出行阻抗值的最大绝对差值.θ和U的取值一般通过乘客出行调查确定,现阶段通常取0.6和10 min.
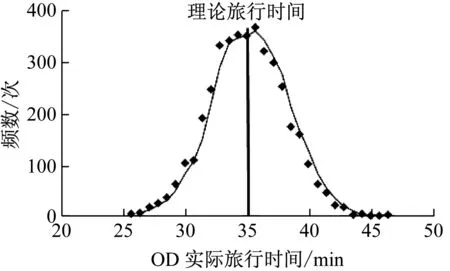
上述生成的有效路径集,在网络规模、复杂程度及时空差异不断加大的情况下,与乘客实际出行不甚吻合的情况时有发生,包括路径的遗漏与多余,且尤以路径遗漏对乘客出行路径选择估计的影响最大,导致后续无法将乘客出行推定到被遗漏的路径上,造成网络客流分布计算的明显偏差.例如,北京地铁网络中的“东直门→大钟寺”OD,如图1所示,按上述现有客流分布模型路径集生成算法得到的有效路径只有唯一一条(路径①,中间换乘1次),但乘客反映及现场调查均发现有可观比例的乘客选择了其他路径(如路径②,中间无换乘).实际上,对该OD间实际旅行时间的统计分析也表明了相类似的结果,如图2所示.
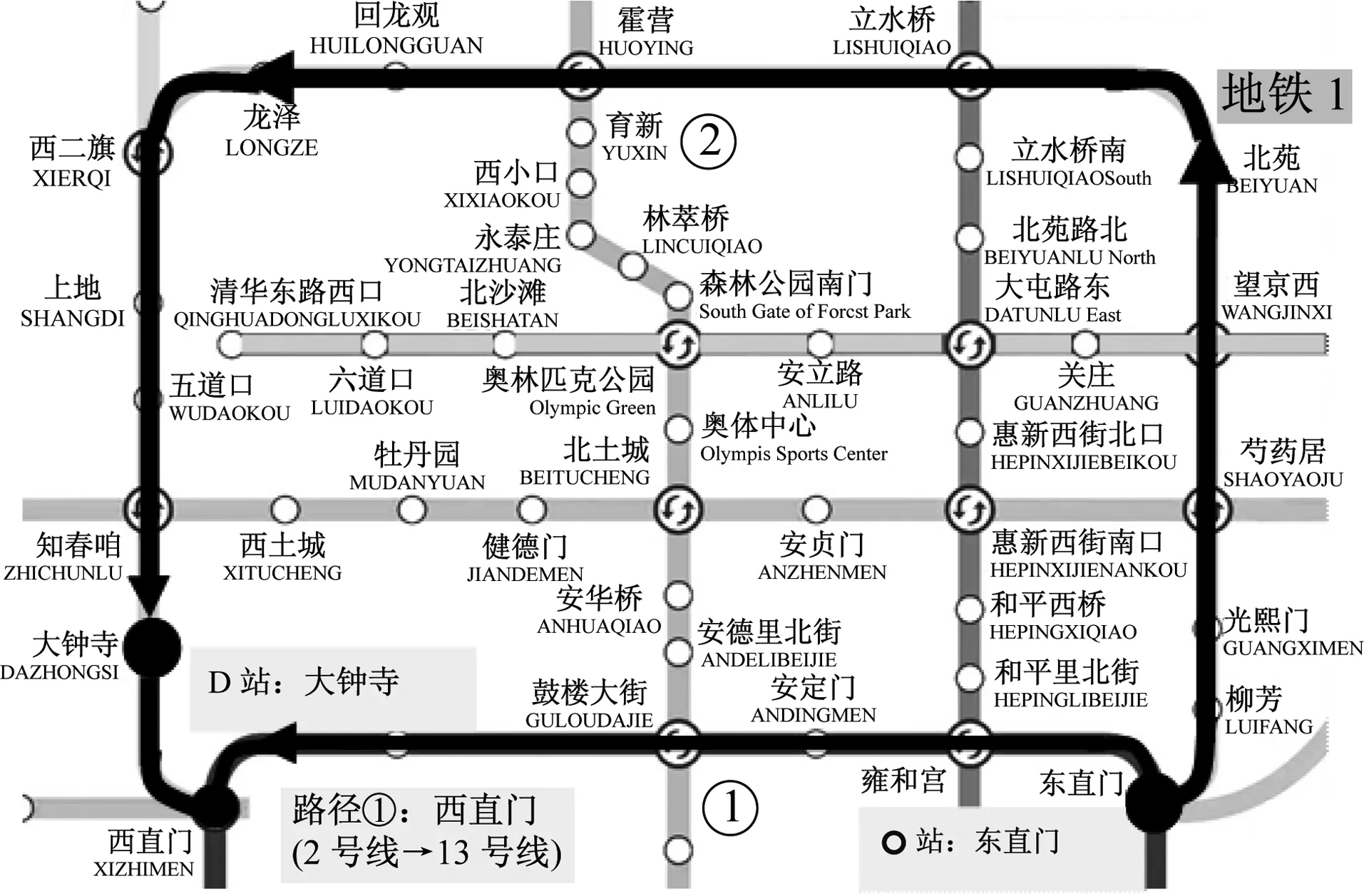
图1 北京地铁“东直门→大钟寺”OD间有效路径与 实际路径示意图
Fig.1EffectivepathinODdistributionmodelandactualpathofBeijingSubway“DongzhimenStation→DazhongsiStation”

图2 北京地铁“东直门→大钟寺”OD间实际旅行时间与 出行路径对应关系
Fig.2CorrespondencebetweentheactualtraveltimeandtravelpathofODbetweenDongzhimenStationandDazhongsiStationinBeijingSubway
为此,引入大数据快速聚类分析算法,通过对AFC票卡数据中提取的实际OD旅行时间的聚类分析,判断有效路径是否遗漏,从而实现对原有清分模型出行路径集的验证.
2 城市轨道交通乘客路径集验证方法
2.1 分析说明
尝试主要利用AFC刷卡记录中提取的实际OD旅行时间数据验证客流分布计算模型中乘客出行路径集是否合理,作为传统基于人工客流调查方法的重要基础(获取调查线索)与补充(进行全网验证).以此为导向,首先对基于OD旅行时间数据分析的出行路径集验证作出如下几点说明:
(1) 路径验证的主要问题:基于城市轨道交通客流分布模型的计算原理,虽然有效路径集生成问题同时包括了路径的遗漏与多余,但是路径多余情况下后续路径选择估计工作具有纠偏作用(因为即便有多余了的路径,在路径选择估计中也不会有显著比例的乘客推定到该路径上去).故实际上的主要问题是路径遗漏,因为对于那些排除在有效路径集之外的路径,乘客是再无可能被推定到其上的.
(2) 主要问题的解决途径:结合现有客流分布模型有效路径集生成方法,遗漏的路径只能是那些与现有路径集中路径阻抗有显著差异(且往往是阻抗较大的)的路径,因为如若差异不大(在最大容许值Tw,range内)则应已包含在现有路径集中了.故提出主要问题的解决途径是,引入快速聚类技术对OD间实际旅行时间数据做聚类分析,获取实际可能的OD间出行路径,比较聚类得到的路径旅行时间与路径阻抗最大容许值之间的大小,从而判断是否存在实际路径遗漏的情况.
(3) 数据驱动分析与客流调查相结合:无论是客流调查还是数据驱动,都并非万能而是特性各异、各有所长,应进行综合利用的研究.由于OD旅行时间本质上是标量数据,故基于实际旅行时间聚类分析的乘客出行路径集验证,无法准确处理路径选择比例估计问题,只能对路径数量异常作出识别,需要与传统客流调查方法相结合,以旅行时间数据驱动分析获取全网络问题OD,在此基础上客流调查跟进并予以重点现场调查与原因分析.本文研究的重点为前者.
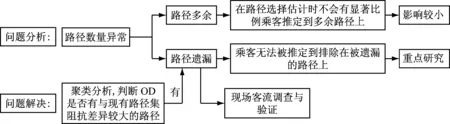
图3 基于旅行时间聚类分析的出行路径集验证说明Fig.3 Illustration of route choice set validation based on travel time cluster analysis
2.2 验证方法
2.2.1数据准备
对于全网络OD,逐一从AFC票卡数据中提取各个OD的实际旅行时间数据,见式3,并按OD保存下来供后续聚类分析使用.考虑到聚类样本量的要求,以最少7个相同特征日(特征日分为工作日(周二~周四)、特殊工作日(周一、周五)、双休日和特定节假日等)的AFC票卡数据来提取OD实际旅行时间数据,即
ti=ti,out-ti,in
(3)
式中:ti为第i张票卡记录的OD实际旅行时间,ti,in和ti,out分别为第i张票卡的进站刷卡时刻和出站刷卡时刻.
2.2.2聚类分析
由于目前国内城市轨道交通客流分布模型路径集以5条路径为上限,为此,以Rodriguez-Laio快速聚类分析算法[9]逐个OD进行聚类分析,获取各个OD实际旅行时间数据的前5位聚类中心以及对应的期望旅行时间Ti(∑i=5).该步骤为路径集验证的核心步骤,具体的Rodriguez-Laio快速聚类分析算法将在2.3节中详细给出.
2.2.3比较验证
(1) 以绝对/相对阈值参数、最短路径阻抗计算OD旅行时间阈值Tmax(式1).相对阈值系数θ为Tw,range与Tw,min的比值,表示有效路径可以超过最短路径出行阻抗值的最大相对比值,通过调查确定,通常取0.6;绝对阈值U为Tw,max与Tw,min的差值,表示有效路径可以超过最短路径出行阻抗值的最大绝对差值,也通过调查确定,通常取10 min.
(2) 将Ti与Tmax逐一进行比较,若Ti均小于Tmax,则原有效路径集通过检验;否则,说明通过聚类分析发现仍有显著比例乘客的实际OD旅行时间超出现有路径集的可能范围,即遗漏了实际路径,对应OD保存至问题OD清单中,输出供进一步的现场客流调查.
2.2.4滚动验证
须注意的是,伴随城市轨道交通网络及客流的变化,乘客在OD间的可能出行路径也在动态变化之中.本方法是一种基于数据驱动的方法,可利用持续积累的海量AFC票卡数据资源,实现对城市轨道交通乘客出行路径集的滚动验证.
2.3 聚类算法
如前所述,AFC票卡保存了包括乘客进出站点及刷卡时分在内的出行信息,据此可以提取较为准确的OD实际旅行时间数据.通过对OD实际旅行时间的统计分析表明,由于OD间各条路径上的出行时耗不同,乘客OD实际旅行时间与其选择的出行路径之间存在一定的对应关系.如图4所示,横坐标为OD实际旅行时间,纵坐标为其相应的频数;图4a为单路径OD的实际旅行时间频数分布情况,近似于围绕其单路径理论旅行时间的正态分布;图4b为三条路径OD的实际旅行时间频数分布情况,频数较为集中的3处分别与3条路径的理论旅行时间相对应.
a 单路径OD

b 多路径OD图4 乘客OD实际旅行时间与出行路径对应关系Fig.4 Correspondence between the actual travel time and travel path of OD
为此,引入大数据分析中的聚类分析技术,从OD实际旅行时间数据中推断OD间乘客实际可能的出行路径选择情况,并与客流分布模型生成的有效路径集进行对比,从而验证其合理性.同时,考虑如下几方面原因,本文采用了Rodriguez-Laio于2014年提出的一种快速聚类算法[9]:OD实际旅行时间数据集呈现“非球面(nonspherical)”的聚类特征,常规的基于欧氏距离的聚类算法无法得到较好的聚类效果;虽然基于密度的聚类算法可以适应“非球面(nonspherical)”聚类特征,但其所需要界定的密度边界值却难以确定;Rodriguez-Laio快速聚类算法克服了上述常规方法的不足,既可以进行“非球面(nonspherical)”聚类也可以自动确定聚类数目,且由于仅需计算数据点之间的“距离”,从而可满足大数据分析在计算时耗上的要求.
Rodriguez-Laio算法的核心思想是:对于数据集而言,某一聚类中心应是它所在类中密度最大的数据点,同时也是距离其他聚类中心相对较远的数据点.具体应用描述如下:在城市轨道交通系统中,通过分析旅行时间总体上呈现的不同波动情况,选取OD对平峰时期乘客的旅行时间作为聚类对象.距离计算即比较多个旅行时间的相似度,将相似度高的对象聚在一起,认为这一类乘客选择同一条路径.
dij=dist(ti,tj)表示乘客i和乘客j的OD旅行时间数据点ti和tj之间的距离,算法采用曼哈顿距离作为数据点间的距离,即
dij=|ti-tj|
(4)
对某OD间的实际旅行时间数据ti,逐一计算其两项指标:局部密度ρi和与高于ti点密度的最小距离δi,而这两项指标均由点距离dij计算得
(1) 局部密度ρi
(5)
其中:
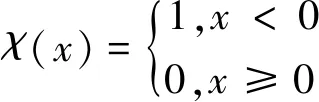
(6)
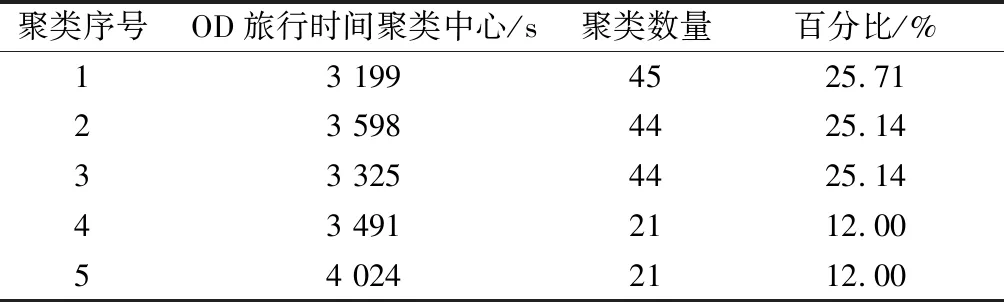
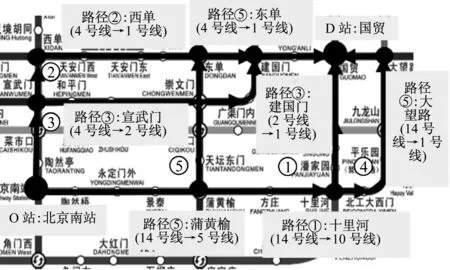
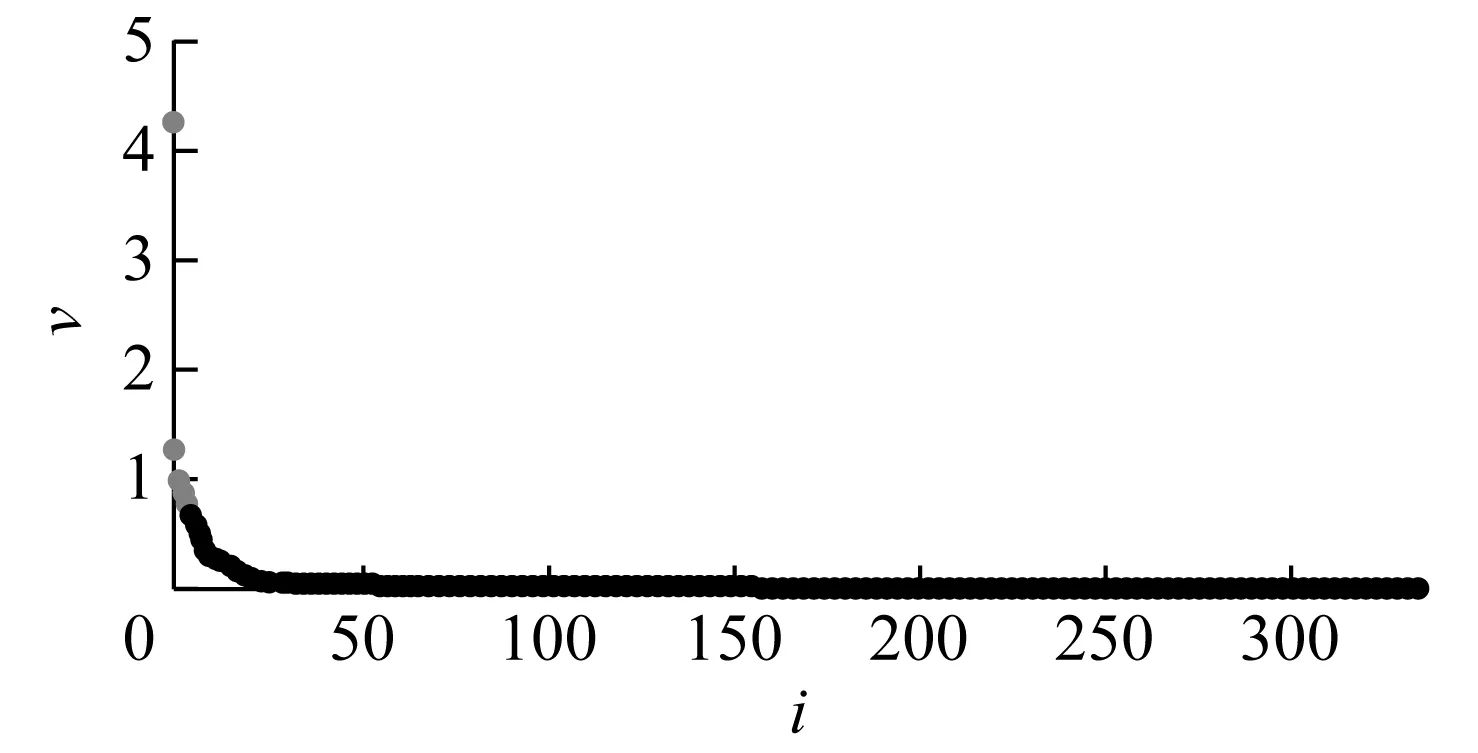
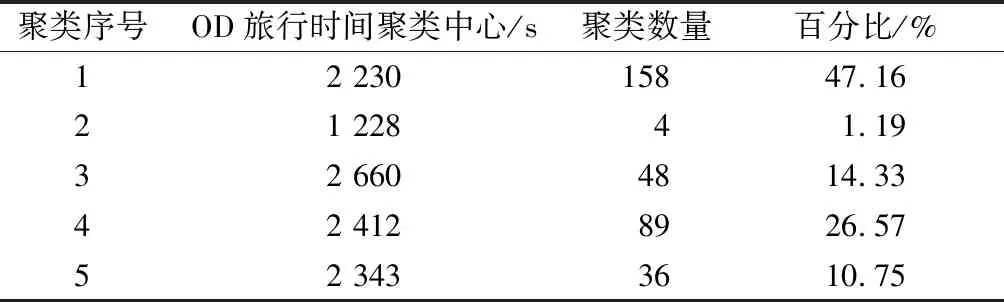
式中:dc为边界距离.对于dij(i (2) 距离δi 旅行时间数据点ti与其他局部密度更大的旅行时间点之间的距离用变量δi来表示,即 (7) 对于某OD而言,其实际旅行时间数据在经过上述Rodriguez和Laio算法进行聚类分析后,可快速获取这些实际旅行时间数据的聚类数及相应的聚类比例. 为了避免在决策图中无法用肉眼判断出聚类中心的情形,引入了一个将ρi值和δi值综合考虑的量,即 γi=ρiδi,i∈IS (8) 以北京地铁网络为例,如图5所示,对上述验证方法进行算例应用及分析.目前北京地铁客流分布模型中路径选择集的最大路径数限制为5条,故选取单路径、多路径和5路径等三类OD进行算例分析,所用数据则为2016年AFC票卡数据[8]. 图5 北京地铁网络(2016年)[10]Fig.5 Beijing Subway network map (2016)[10] (1) 单路径OD(2号线北京站→13号线回龙观) 在北京地铁客流分布模型生成的有效路径选择集中,“2号线北京站→13号线回龙观”为仅有1条有效路径的单路径OD,如表1和图6所示. 但是,以该OD上AFC票卡数据提取的实际旅行时间数据聚类分析得到的结果如图7和表2所示.图7a显示了每个旅行时间数据点i的局部密度值ρi和与高于该点密度的最小距离值δi;图7b则显 表1北京地铁客流分布模型中“2号线北京站→13号线回龙观”的有效路径选择集 Tab.1AneffectiveroutechoicesetforLine2BeijingStation→Line13HuilongguanStationinBeijingSubwaypassengerflowdistributionmodel 路径序号所经站点路径阻抗1北京站—2号线—东直门—13号线—回龙观2 603 s 注:路径①为现有路径,路径②和③为实际存在的其他路径图6 “2号线北京站→13号线回龙观”出行路径示意Fig.6 Route map of Line 2 Beijing Station→Line 13 Huilongguan Station 示了每个旅行时间数据点i的γi值,γi值越大则该数据点i越可能是聚类中心,本例中取前5位数据点.从表2结果中可以发现,仍有大比例乘客实际旅行时间大于阈值,表明还存在其他出行路径.事实上,通过现场跟踪调查也确实发现了乘客在出行过程中实际存在多于1条的其他路径(如图6中的路径②和路径③). (2) 多路径OD(4号线北京南站→1号线国贸) 在北京地铁客流分布模型生成的有效路径选择集中,“4号线北京南站→1号线国贸”为有4条有效路径的多路径OD,如表3和图8所示. 但是,以该OD上AFC票卡数据提取的实际旅行时间数据聚类分析得到的结果如图9和表4所示.从表中可以发现,仍有大比例乘客实际旅行时间大于阈值,表明还存在其他出行路径.事实上,通过现场跟踪调查也确实发现了乘客在出行过程中实际存在多于4条的其他路径(如图8中的⑤路径). a 点和函数 b 聚类排序图7 “2号线北京站→13号线回龙观”OD实际旅行 时间聚类分析Fig.7 Actual travel time cluster analysis chart of Line 2 Beijing Station→Line 13 HuiLongGuan Station表2 基于实际旅行时间聚类分析的“2号线北京站→13号 线回龙观”路径集验证结果 Tab.2VerificationresultsofthepathchoicesetforLine2BeijingStation→Line13HuilongguanStationbasedontheclusteranalysisofactualtraveltime 聚类序号OD旅行时间聚类中心/s聚类数量百分比/%13 1994525.7123 5984425.1433 3254425.1443 4912112.0054 0242112.00 注:由于北京地铁路径集限制在5条以内,故取聚类分析得到的前5个聚类中心进行聚类结果统计;表中2,3,4,5为聚类中心值超过阈值,从而表明实际中选择了其他出行路径的数据类. 表3北京地铁客流分布模型中“4号线北京南站→1号线国贸”的有效路径选择集 Tab.3AneffectiveroutechoicesetforLine4BeijingSouthRailwayStation→Line1GuomaoStationinBeijingSubwaypassengerflowdistributionmodel 路径序号所经站点路径阻抗1北京南站—14号线—十里河—10号线—国贸1 423 s2北京南站—4号线—西单—1号线—国贸1 738 s3北京南站—4号线—宣武门—2号线—国贸1 741 s4北京南站—14号线—大望路—1号线)—国贸1 911 s 注:路径①②③④为现有路径,路径⑤为实际存在其他路径图8 “4号线北京南站→1号线国贸”出行路径示意图Fig.8 Route map of Line 4 Beijing South Railway Station →Line 1 Guomao Station a 点和函数图 b 聚类排序图图9 “4号线北京南站→1号线国贸”OD实际旅行时间 聚类分析 Fig.9ActualtraveltimeclusteranalysischartofLine4BeijingSouthRailwayStation→Line1GuomaoStation 表4基于实际旅行时间聚类分析的“4号线北京南站→1号线国贸”路径集验证结果 Tab.4VerificationresultofthepathchoicesetforLine4BeijingSouthRailwayStation→Line1GuomaoStationbasedontheclusteranalysisofactualtraveltime 聚类序号OD旅行时间聚类中心/s聚类数量百分比/%12 23015847.1621 22841.1932 6604814.3342 4128926.5752 3433610.75 注:由于北京地铁路径集限制在5条以内,故取聚类分析得到的前5个聚类中心进行聚类结果统计;表中3,4,5为聚类中心值超过阈值,从而表明实际中选择了其他出行路径的数据类. (3) 5路径OD(9号线六里桥东→2号线东直门) 在北京地铁客流分布模型生成的有效路径选择集中,“9号线六里桥东→2号线东直门”为有5条有效路径的多路径OD,如表5和图10所示. 表5北京地铁客流分布模型中“9号线六里桥东→2号线东直门”的有效路径选择集 Tab.5AneffectiveroutechoicesetforLine9LiuliqiaoEastStation→Line2DongzhimenStationinBeijingSubwaypassengerflowdistributionmodel 路径序号所经站点路径阻抗1六里桥东—9号线—国家图书馆—4号线—西直门—2号线—东直门2 235 s2六里桥东—9号线—白石桥南—6号线—车公庄—2号线—东直门2 439 s3六里桥东—9号线—北京西站—7号线—菜市口—4号线—宣武门—2号线—东直门2 429 s4六里桥东—9号线—白石桥南— 6号线—朝阳门—2号线—东直门2 585 s5六里桥东—9号线—军事博物馆—1号线—建国门—2号线—东直门2 603 s 但是,以该OD上AFC票卡数据提取的实际旅行时间数据聚类分析得到的结果如图11和表6所示.从表中可以发现,仍有大比例乘客实际旅行时间大于阈值,表明还存在突破最大数值5条以外的其他出行路径.事实上,通过现场跟踪调查也确实发现了乘客在出行过程中实际存在多于5条的其他路径(如图10中的路径⑥). 该算例通过对OD实际旅行时间数据的聚类分析,识别出有显著比例的乘客实际出行时间超过了现有路径阻抗最大容许值,从而发现实际存在其他可能的出行路径选择.上述乘客路径集验证结果可对该类异常OD作出识别,对全网络验证分析后得到的路径集问题OD清单为以原因分析为导向的现场客流调查与模型修正提供了重要参考. 注:路径①②③④⑤为现有路径,路径⑥为实际存在的其他路径 图10“9号线六里桥东→2号线东直门”出行路径示意图 Fig.10RoutemapofLine9LiuliqiaoEastStation→Line2DongzhimenStation a 点和函数 b 聚类排序图11 “9号线六里桥东→2号线东直门”OD实际旅行 时间聚类分析图 Fig.11ActualtraveltimeclusteranalysischartofLine9LiuliqiaoEastStation→Line2DongzhimenStation7 表6基于实际旅行时间聚类分析的9号线六里桥东→2号线东直门”路径集验证结果 Tab.6VerificationresultofthepathchoicesetforLine9LiuliqiaoEastStation→Line2DongzhimenStationbasedontheclusteranalysisofactualtraveltime 聚类序号OD旅行时间聚类中心/s聚类数量百分比/%13 128 s2116.8023 614 s2318.4033 248 s4636.8042 950 s1512.0052 770 s2016.00 注:由于北京地铁路径集限制在5条以内,故取聚类分析得到的前5个聚类中心进行聚类结果统计;表中1,2,3为聚类中心值超过阈值,从而表明实际中选择了其他出行路径的数据类. 城市轨道交通乘客出行路径集是否正确,是乘客路径选择估计乃至网络客流分布计算的前提和基础,轨道交通网络规模和结构以及客流出行特征的动态变化性要求对乘客路径集进行滚动检验与修正.本文研究提出了一种基于OD实际旅行时间聚类分析的城市轨道交通乘客路径集验证方法,可以在全网络范围内对路径选择集问题OD作出快速识别及滚动验证.该方法在北京地铁网络中进行了初步应用,并为以原因分析为导向的现场客流调查与模型修正提供重要参考,取得了较好的效果.未来正在进行的另一项研究工作是,结合ATS实际运行图等数据资源,在路径集验证基础上进一步对乘客路径选择估计比例作出检验与修正.
3 算例分析












4 结语

