煤矿井下定向钻孔轨迹预测方法研究

孙 涛，吝伶艳，刘宗伟，宋建成，王 雪

(1.太原理工大学 矿用智能电器技术国家地方联合工程实验室，山西 太原 030024； 2.太原理工大学 煤矿电气设备与智能控制山西省重点实验室，山西 太原 030024)

煤矿水平定向长钻孔现已成为国内外地质勘探、瓦斯抽放的主要技术途径。现有的煤矿近水平千米定向钻机的轨迹控制方案主要是司钻人员通过随钻测斜系统观察实钻轨迹与设计轨迹间偏差的大小与方向，再根据操作经验在添加钻杆时调整工具面角，完成实钻轨迹对设计轨迹的跟踪[1]。这种操作方式经验性较强，容易造成实钻轨迹偏离设计轨迹、钻具摩阻力偏大等问题，影响钻井效率。因此有必要开展煤矿近水平定向钻机轨迹控制技术的研究，而钻孔轨迹预测作为轨迹控制的前提，自然成为了钻探技术研发中的重点[2]。

自20世纪50年代美国学者Lubinski将钻孔轨迹预测技术引入石油领域以来，钻孔轨迹预测技术进入了蓬勃发展期，如B.H.Walker根据最小势能法将钻具的力学分析突破至三维领域；我国的白家祉教授根据纵横弯曲梁理论将三弯矩方程引入钻具的静力学分析中，迄今已形成一个较完善的理论体系。但值得注意的是，定向钻井技术于20世纪60年代由美、德等国家从石油领域引入煤矿领域后，单弯螺杆钻具与随钻测量系统的组合凭借更为优秀的造斜率与可控性，已取代移植于石油领域的稳定组合钻具，成为了目前煤矿施工的主流[4]，与此同时，煤矿施工在施工工艺上与石油领域也有较大不同。这种现状造成目前主流的钻孔轨迹预测方法往往难以应用于煤矿施工。

针对上述问题，本文以纵横弯曲梁理论为基础，对三点定圆法进行改进，提出一种适用于煤矿近水平千米定向钻机的轨迹预测方法。基于MATLAB搭建轨迹预测模型，经验证明该方法的预测精度能满足施工要求，并高于传统纵横弯曲梁理论和钻头与地层相互作用模型结合的方法(后文简称纵横弯曲梁法)。

1 基础理论

1.1 基础方法

三点定圆法认为钻具组合与井壁接触的三点处于一个曲率稳定的圆弧上，以结构弯角的大小与3个接触点间的距离来定义钻具的造斜率K[6]：

(1)

式中，K为钻具造斜率；V为结构弯角大小；L1为钻头到下稳定器距离；L2为下稳定器到上稳定器距离。

由式(1)可知，三点定圆法的应用对象原为带稳定器钻具，在计算方式上明显未考虑钻具的受力变形对造斜率的影响，且当上稳定器位置固定不变时，移动下稳定器不改变钻具造斜率，明显与实际不符。

纵横弯曲梁法认为钻柱组合在受力弯曲变形后形成若干个受纵横弯曲载荷的简支梁柱，利用连续条件、边界条件导出三弯矩方程，再通过三弯矩方程求取钻头侧向力，并与三维钻速方程结合，实现钻孔轨迹的预测。该理论能很好地计算钻井工艺参数、各段钻铤长度及线重量、已钻井眼轨迹、钻具姿态、结构弯角等参数对井眼轨迹的影响，分析过程清晰明了，计算简便。但三维钻速方程中的地层各向异性指数、钻头各向异性指数难以获取，给该理论的实际应用带来了困扰。

1.2 三点定圆法的改进

图1所示为单弯螺杆钻具结构。根据纵横弯曲梁理论，煤矿近水平定向钻机适用的单弯螺杆钻具在钻进过程中受力发生弯曲变形，与井壁产生接触，被钻头、结构弯角肘点、上切点分为两跨，此时可将L1视为钻头到结构弯角肘点距离，L2视为结构弯角到上切点距离，这样就为三点定圆法应用于单弯螺杆钻具提供了前提条件。而单弯螺杆钻具结构弯角V、钻头到结构弯角肘点距离L1是固定不变的，因此此时决定钻具造斜率的唯一参数变为表征上切点位置的L2，若能计算出不同条件下BHA(孔底钻具组合)受力弯曲形成的上切点位置，就可预测不同工具面角、钻压下的钻具造斜率，从而实现钻孔轨迹预测。

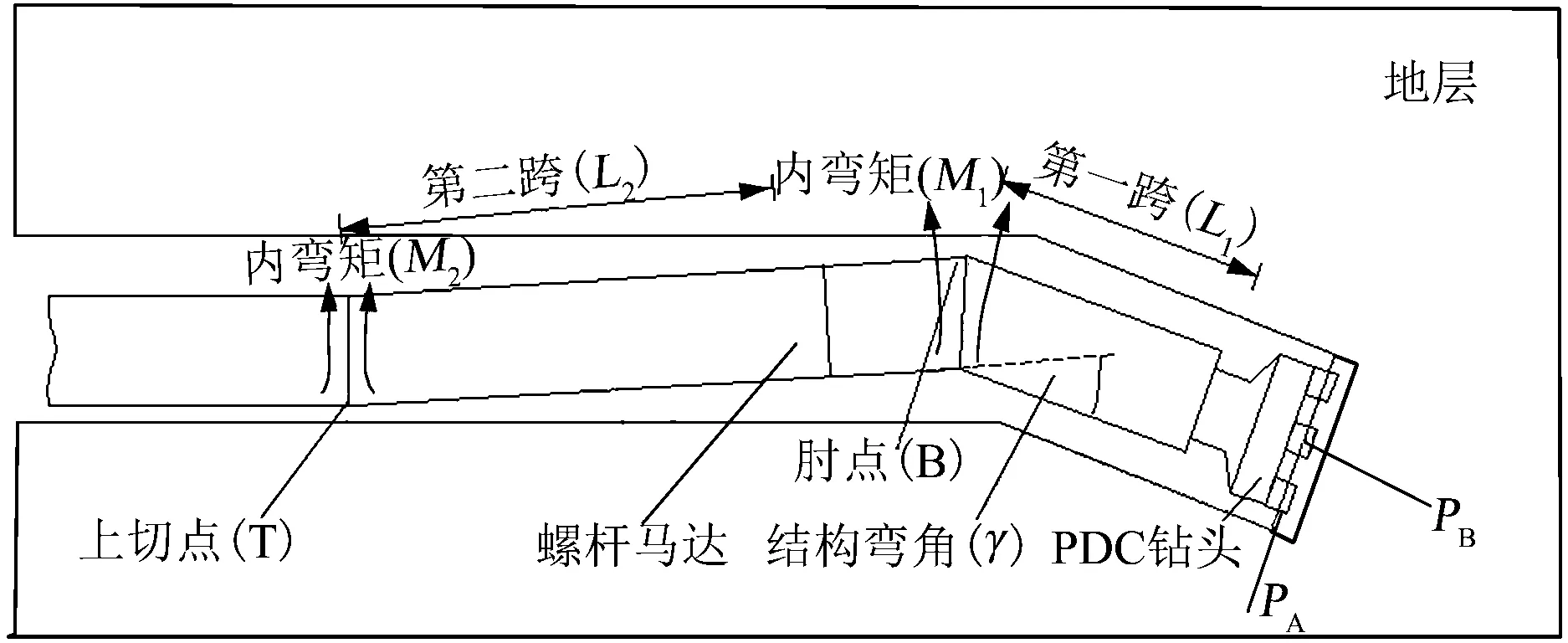
图1 单弯螺杆钻具结构

2 模型的建立

2.1 BHA的受力分析

将千米钻机适配的单弯螺杆钻具作为对象进行受力分析[7]，如图1所示，基于纵横弯曲梁法，底部钻具组合在受力弯曲变形后将被钻头、结构弯角点以及上切点分为受纵横弯曲载荷的两跨，附加内弯矩M1后，通过弹性稳定理论可求得每跨端部的转角值，再根据相邻跨连接点处转角相等的稳定条件以及上切点处的边界条件便可导出三弯矩方程组。在此方程组中内弯矩M1、第二跨跨长L2为待求量。

2.2 二维井身内三弯矩方程的建立

为描述清晰，先对二维井身内的BHA作受力分析，二维井身意为工具面角保持不变且与井身平面同面，为利用纵横弯曲梁理论进行受力分析，引入了梁柱稳定系数u以及放大因子X(u)，Y(u)，Z(u)等计算参数，具体计算方式如下：

对任一跨梁柱而言，当施加在此段梁柱上的平均压力值P>0时：

(2)

由梁柱弹性稳定理论可知，当第一、二跨梁柱受力弯曲达到稳定状态时：

第一跨右端转角：

(3)

第二跨左端转角：

(4)

第二跨右端转角：

(5)

如图1，将连续梁柱从结构弯角处断开，并附加内弯矩M1，则B点处的连续条件为：

(6)

上切点处的边界条件为：

(7)

由此可得到三弯矩方程组：

(8)

上述等式中，K为井身曲率；L1，L2分别为第一、二跨跨长；q1，q2分别为第一、二跨梁柱横向均布载荷集度；M1，M2分别为结构弯角、上切点处内弯矩；I1，I2分别为第一、二跨梁柱等效截面轴惯性矩；EI1，EI2分别为第一、二跨梁柱等效抗弯刚度；y0，y1，y2分别为钻头中心纵坐标(一般取0)、结构弯角肘点纵坐标、上切点纵坐标；γ为结构弯角值。

具体计算方法如下：

(9)

式中，LA，LB为两测点A，B的井深；αA，αB为相邻两测点对应的井斜角；ρ为曲率半径；PB为钻压；α0为钻头处的井斜角；ω1，ω2为第一、二跨在梁柱钻井液中的线重量；D0为井径；Ds1为结构弯角处截面直径；DC2为第二跨梁柱直径。

根据三弯矩方程，由式(2)得出M1关于L2的表达式，代入式(1)中，通过预设收敛精度，即可根据二分法求得表征上切点位置的参数L2以及结构弯角处的内弯矩M1。

2.3 三维井身内的BHA受力分析

由于结构弯角的存在，底部钻具组合形成工具平面，随着工具面角的转动，工具平面与井身斜平面R产生夹角，井身斜平面对钻具的约束必然会发生改变，上切点的位置也会随之发生改变。因此，需要对三维空间内钻具组合进行受力分析，计算采用不同工具面角时的第二跨L2的值。为简化计算，如图2，将空间内受力变形的三维问题分解为井斜平面P(过直线AB的铅锤平面)与方位平面Q(过直线AB与P平面正交)内的两个二维问题，A，B为选取的两测点，相关参数根据随钻测量系统获取，并在P平面内求取下一工具面角时的L2值。

图2 R，P,Q三平面的定义

P平面内的三弯矩方程为：

(10)

上式中：

(11)

式中，δ为R平面与P平面夹角；Ω为工具面角；y1P，y2P中的正负关系由结构弯角肘点位置判断，以上(内)为正。

同上，预设收敛精度后，采用二分法可求得待求量L2值。

至此，可通过纵横弯曲梁法，构建三弯矩方程，求取当前施工工具面角下的第二跨跨长L2。根据三点定圆法，将L2代入式(1)可求取此时的造斜率K。

2.4 预测倾角、方位角的计算

当预测造斜率已知时，即可根据已钻钻孔数据计算下一测点的预测倾角、方位角。

下一测点倾角：

θn+1=θn+arcsin(sin(KΔL)cosΩn)

(12)

下一测点方位角：

αn+1=αn+arcsin(sin(KΔL)sinΩn)

(13)

式中，θn+1，αn+1为下一测点预测倾角、方位角；θn，αn为当前测点倾角、方位角，ΔL为钻杆长度，Ωn为下一钻杆采用的工具面角。

2.5 预测姿态数据的处理

为更直观地表现预测轨迹相对于实际轨迹的贴近程度，需要将预测结果以轨迹坐标的形式表达出来。基于平衡正切法，可由预测姿态数据与已钻钻孔轨迹数据计算得到下一测点在孔口坐标系下的预测坐标值：

(14)

式中，xn+1，yn+1，zn+1分别为下一测点的三轴坐标预测值；xn，yn，zn分别为当前测点的三轴坐标测量值。

至此，钻孔轨迹预测模型建立完毕。当根据钻具的姿态数据以及已钻井眼轨迹数据，即可算得采用不同工具面角、钻压时下一测点的预测坐标。

3 与传统纵横弯曲梁法对比验证

传统纵横弯曲梁法的预测精度依赖于钻头各向异性指数、地层各向异性指数这两类参数值的准确测量。前者表征BHA采用钻头轴向与侧向切削能力的差异，由实验测取。后者表征地层可钻性在倾向、法向、走向上的分布特性，由井史数据推算。

采用山西晋城赵庄矿提供的钻孔数据对模型预测精度进行验证，数据来源井段最大钻深为434m，采用的钻具为1.5°的单弯动力钻具，适配的钻头为96mm去芯PDC钻头，施工方案为每两根钻杆(6m)调整一次工具面角。验证方案为：以已钻钻孔轨迹姿态数据、施工参数(主要为钻压)为输入，下一测点的预测坐标为输出，与实钻轨迹中下一测点的轨迹坐标进行对比。将两种方法的预测结果进行对比验证(图3)，完成预测精度验证。

图3 与传统纵横弯曲梁法对比

由图3可知，方位角、倾角预测相对误差基本保持在1%以下；由预测方位角、预测倾角计算得来的下一点预测坐标距设计坐标的绝对误差基本稳定在0.05m左右，有少量测点的绝对误差达到了0.2m以上，分析是由于该部分井段地层分布发生了较大变化，对轨迹形成产生了影响。

在两种预测方法的对比中，经纵横弯曲梁理论改进后的三点定圆法在预测精度上明显优于传统的纵横弯曲梁法(表1)。两者的预测精度差距主要体现在倾角的预测误差上，差距在10倍左右，而方位角预测误差相近，这是由于选取的验证井段的造斜率主要落在变倾角率上，而变方位率很小，当两者预测造斜率误差相近时，归算得到的预测方位角就会出现大小相近的误差。

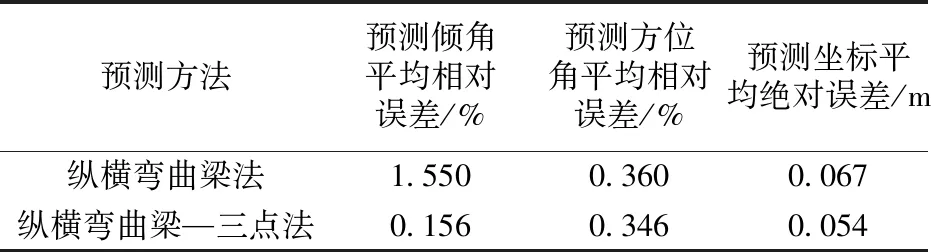
表1 预测精度数据对比

4 结 论

(1)经改进后的三点定圆法每两根钻杆(6m)的预测绝对误差保持在0.05m 左右，预测精度达到了煤矿井下施工要求。

(2)当传统纵横弯曲梁法中相关参数难以测取或取准时，经改进后的三点定圆法在易于实现的同时，有着精度上的优势。

(3)由于本文所提出的经改进后的三点定圆法是通过计算钻具组合在不同弯曲形状下的造斜率来实现轨迹预测，并未考虑地层因素的影响，因此当钻孔延伸至地层变化幅度较大的区域时，预测精度可能会受较大影响。