单一裂纹几何特征对岩石力学性质影响程度研究
张艳博,刘志超,梁 鹏,姚旭龙,田宝柱,刘祥鑫
(1.华北理工大学 矿业工程学院,河北 唐山 063009;2.华北理工大学 河北省矿业开发与安全技术重点实验室,河北 唐山 063009)
1 概 述
岩石是矿山工程的主要施工环境,其物理力学性质和内部损伤特征关系着工程的稳定以及生产的安全,现有的众多研究结果表明[1-6]:岩石宏观的失稳破坏通常是由于内部缺陷的张开、闭合、扩展和贯通引起的。而岩石又是一种复杂的天然介质,其内部分布着众多不同几何特征的裂纹缺陷,这些不同特征的损伤使得岩石的力学性质和变形破坏规律变得更加复杂。裂纹的尺寸、角度、分布位置作为裂纹的自身属性,共同决定了裂纹的几何形态以及分布状态。因此开展研究裂纹的几何特征对岩石损伤程度的影响研究对于揭示岩石损伤演化机理及岩石力学性质评定具有重要的科研意义。
现阶段研究已经发现,裂纹的尺寸、角度、分布位置的改变对于岩石的物理性质、损伤演化特征产生了巨大的影响。尚黎明等[7]利用红砂岩制作了含三维内置裂隙的圆柱体试件,通过试验和裂隙扩展后的CT图像扫描分析,结合裂隙扩展的数值模拟,研究了在单轴压缩条件下裂隙尺寸的变化对岩石裂隙扩展、破坏规律和应力分布的影响;惠鑫等[8]考虑节理裂隙尺寸为分形分布和方位为正态分布的情况,建立岩石统计损伤本构模型,给出与裂隙尺寸、尺寸分形维数和产状相关的本构模型参数,讨论了模型参数的物理意义和影响因素;林鹏等[9]通过自制的试验系统以及数值模拟,研究了不同角度的预置单裂纹缺陷的花岗岩试样的裂纹扩展与破坏过程,结果表明裂纹扩展和最后的破坏行为受预置单裂纹缺陷的角度影响;朱谭谭等[10]在板状砂岩试样内预制了圆孔和裂隙组合型缺陷,通过室内单轴压缩试验,研究了裂隙倾角和裂隙长度对砂岩强度特征、变形特征及破裂演化过程的影响规律。
从上述可知,现阶段对于裂纹几何特征对岩石物理力学性质影响研究,多进行如裂纹倾角、长度等单一几何特征对岩石力学影响实验分析,并未考虑多种因素共同作用的影响以及不同几何特征对力学性质影响程度的差异性。而实际生产中,由于裂纹损伤的随机分布特性,其几何特征是由长度、倾角、位置多因素共同作用的。因此探讨天然裂纹损伤对岩石性质的影响,应考虑不同几何特征对其影响的差异性,而现有成果缺少探讨裂纹不同几何特征对岩石力学性质影响显著性的研究。
由于岩石材料的不均匀性及各向异性,为剔除干扰因素的影响,以及考虑正交实验组数、重复次数数量大,本文通过RFPA数值模拟软件开展包含裂纹长度、倾角、分布位置的预制单裂纹正交试验,采用方差分析的方法探究裂纹长度、倾角、位置对岩石力学性质的影响显著性。
2 实验设计
2.1 RFPA模型参数设置
模型整体尺寸设为100mm×120mm,模型网格划分为200×240的单元网格。其中中央位置100mm×100mm为岩石基质材料,在其上下分别设置10mm×100mm的钢板进行刚性约束(见图1)。设定岩石模型力学参数符合威布尔统计分布规律,岩石材料的破坏准则选为莫尔-库伦准则。为确保实验不受岩石基质材料随机生成分布的影响,所有对照组实验均基于同一个基质材料模型进行。

图1 含预制裂纹数值模型示意
2.2 材料力学性质及试验加载设置
经室内花岗岩物理力学实验测定,其物理学参数设置为:弹性模量6000MPa、单轴抗压强度为200MPa、泊松比为0.25、内摩擦角为45°。岩石RFPA模拟相变准则参数控制参数设置为:压拉比为10、残余泊松比系数为1.1、残余强度百分比为0.1、最大压应变系数为200、最大拉应变系数为1.5、相变准则为库伦准则。加载方式设为y轴方向的位移增量单轴加载,位移增量为0.02mm/步,预设加载步数为1000步,当试件完全破坏时停止加载。
2.3 实验方案
裂纹的几何特征是由长度、倾角以及分布位置3个参数决定的,这些几何特征的改变将影响岩石的物理力学性质。为了探究影响裂纹几何特性的不同因素的改变对岩石物理性质的影响程度,因此在岩石材料内部预制包含上述几何特征的初始单裂纹,裂纹设置形式如图1所示。
(1)裂纹尺寸对岩石力学性质影响实验
预制单裂纹位于模型中央,分布位置y设为50mm,裂纹角度β设置为45°,裂纹长度x分别设置为10mm,15mm,20mm,25mm,30mm。探究裂纹尺寸的改变对岩石峰值强度的影响。
(2)裂纹角度对岩石力学性质影响实验
预制单裂纹设置在位置y为50mm处,裂纹长度x设为20mm,倾角β分别设为15°,20°,25°,30°,35°,40°,45°,50°,55°,60°,65°。探究裂纹角度的改变对岩石峰值强度的影响。
(3)裂纹分布位置对岩石力学性质影响实验
预制裂纹长度x设置为20mm,角度设置为45°,分布位置y设为10mm,15mm,20mm,30mm,40mm,50mm,60mm,70mm,80mm,85mm,90mm。探究裂纹分布位置的改变对岩石峰值强度的影响。
(4)裂纹多几何特征正交试验
正交试验设置裂纹尺寸、倾角、分布位置3个影响因素作为正交实验指标,各因素水平见表1,其中裂纹长度x设置15mm,20mm,25mm 3种水平;裂纹倾角β设置15°,30°,45°,60°4种水平;裂纹距试件端部y设置16.67mm,33.33mm,50mm 3种水平。正交试验总共进行36组,每组实验因素水平见图2。
实验能够较好反映出不同实验因素水平下花岗岩应力曲线、试件模型峰值应力以及预制初始裂纹的扩展变化过程,以裂纹长度x为20mm、位置y为50mm、裂纹倾角β为60°的试件为例,结果见图3。

表1 正交试验各因素水平
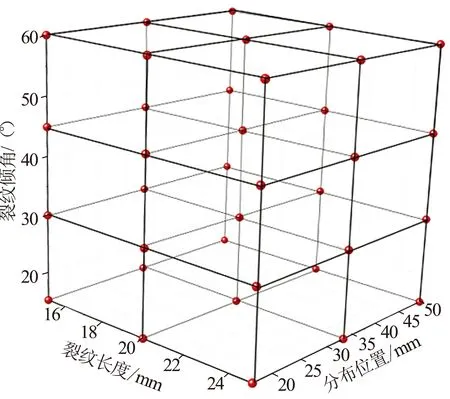
图2 正交试验因素水平

图3 加载过程步数-应力
3 裂纹单因素几何特征对岩石峰值应力影响分析
3.1 裂纹长度、角度对岩石峰值应力的影响
图4为当裂纹倾角β为45°,裂纹位置y取值为50mm时岩石峰值强度随裂纹长度变化趋势图。从图中可得到当其他几何特征一定时,岩石的峰值应力随预制裂纹尺寸的增大呈现降低趋势,且峰值应力随长度的改变下降幅度较大。

图4 预制裂纹长度与峰值强度变化曲线
图5是裂纹长度x为20mm,位置y为50mm时,倾角β分别设为15°,20°,25°,30°,35°,40°,45°,50°,55°,60°,65°时峰值应力随角度变化曲线。从图中可知随着预制裂纹角度的增加,岩石模型的峰值应力呈增加趋势,且应力上升幅度随角度的增加逐步变大。

图5 预制裂纹倾角与峰值强度变化曲线
3.2 裂纹分布位置对岩石峰值应力的影响
为进一步探究预制裂纹位置对于岩石峰值应力的影响,设置了不同位置的预制单裂纹,裂纹长度x为20mm,倾角β为45°,位置y数值设为10mm,15mm,20mm,30mm,40mm,50mm,60mm,70mm,80mm,85mm,90mm。本文划分生成了3次模型网格,得到3组重复试验下岩石峰值应力及其平均值随裂纹变化曲线,如图6所示。从图中可以看出3次重复实验结果及其平均值的曲线趋势大致相同,整体呈“U”字型,即在靠近试件两端的区域表现为裂隙距端面距离越短岩石的峰值强度越高,在试件的中心区域岩石的峰值应力随裂隙的位置改变呈波动状态。


图6 含不同位置裂纹岩石峰值应力变化曲线
预制裂纹位置对试件峰值应力的影响可分为2个区域,在距试件端部20mm以内为岩石峰值应力随距端部的距离增加呈单调降低趋势,预制裂纹在试件内部区域,试件的峰值应力整体呈较低水平且位置的改变对其影响较弱,整体呈波动状态。因此认为在岩石内部,裂纹位置对岩石力学性质影响较弱,为进一步验证假设,开展了裂纹位置对岩石峰值应力影响进行主效应检验。主效应是描述1个自变量的改变对因变量影响大小的度量,将所有位置以及剔除端部的位置进行主效应检验见表2、表3。当包含岩石端部区域时,显著性数值为小于0.05,说明在95%置信区间下裂纹位置的改变对岩石峰值应力影响显著。当预制裂纹位置剔除端部区域之后,显著性数值为0.235大于0.05,说明在95%置信区间下岩石峰值应力的变化与裂纹位置的改变无关,峰值应力的改变是由实验组间误差引起的,显著性检验结果与实验结果一致。

表2 剔除端部单因素方差分析
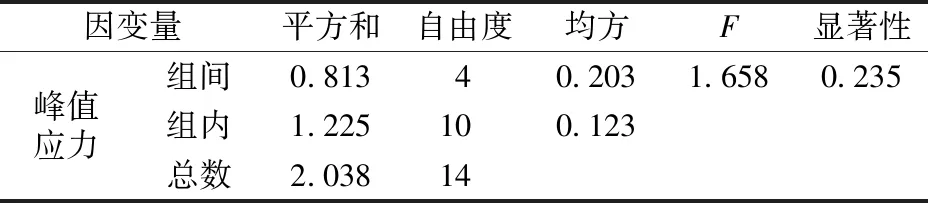
表3 包含所有位置单因素方差分析
4 裂纹几何特征对岩石力学性质影响程度分析
4.1 裂纹几何特征对岩石力学性质影响显著性检验
方差分析的基本思想是:通过分析研究不同来源的变异对总变异的贡献大小,从而确定可控因素对研究结果影响力的大小[11-13]。为探究裂纹长度、倾角、分布位置对岩石峰值应力影响程度大小,通过方差分析对该3个几何特征进行显著性检验。正交实验中因素裂纹尺寸记为因素A有3个水平、分布位置记为因素B含3个水平、角度记为因素C具有4个水平,如图2所示,实验结果如图7所示。
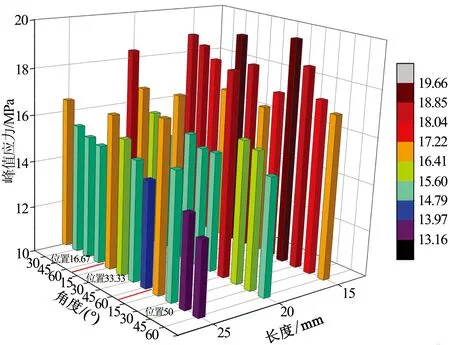
图7 正交试验结果分布
由于裂纹长度、倾角、分布位置3个几何特征之间互不影响,且在某一正交水平下重复实验,实验样本之间相互独立,实验结果符合正态分布。因此该实验满足进行方差分析的必要条件,可以得到以下关系:
(1)
式中,σ为实验结果岩石峰值应力的一般平均;a,b,c分别为3种影响因素的自由度;σi..表示峰值应力在裂纹长度为第i水平的均值;σ.j.表示峰值应力在裂纹角度为第j水平的均值;σ..k表示峰值应力在位置为第k水平的均值;αi为影响因素裂纹长度在第i水平下的水平效应;βj为裂纹位置在第j水平下的水平效应;γk为裂纹倾角在第k水平下的水平效应。
以裂纹长度为例,来求证裂纹尺寸的变化对岩石峰值强度影响是否显著,其等价于检验假设裂纹尺寸在各水平下的水平效应是否为零,即
H0∶α1=α2=…=αi=0
(2)
检验上述假设的基本思想,是将岩石峰值应力的总离差平方和分解为裂纹尺寸、分布位置、角度因素影响产生的离差平方和以及随机误差产生的离差平方和。
(3)

(4)
式中,SSA为裂纹尺寸影响产生的离差平方和表示裂纹长度的改变对峰值应力变化产生的影响;SSB,SSC分别为裂纹位置、裂纹角度产生的离差;SSE为实验误差产生的离差;SST为岩石峰值应力的整体离差平方和。若上式成立,则根据Cochran定理,可以证明仅当假设H0成立时,裂纹长度影响产生的离差平方和SSA与随机误差产生的离差平方和SSE有以下分布规律:
(5)
且式(5)之间相互独立,则裂纹长度产生的SSA与实验误差产生的SSE之间有以下分布式:
(6)
通过查表可以获得临界值Fα,当FA值大于Fα时,拒绝H0因素A影响显著,反之接收H0影响不显著。裂纹尺度的FA值为75.663>3.34,则证明裂纹长度的改变对于岩石峰值应力的结果影响显著。同理可得岩石分布位置的改变对岩石峰值应力影响不显著FB(1.373)

表4 主体间效应的检验
裂纹不同几何特征对岩石峰值应力影响程度正交试验方差分析结果表明:在置信区间为95%的情况下裂纹的长度、角度的改变对试件峰值强度的影响极为显著,裂纹位置的改变对峰值强度的影响不显著,裂纹位置的改变对岩石峰值强度影响不明显。通过上文得到岩石峰值应力随裂纹单一影响因素变化特征可以看出:预制裂纹尺寸的改变对岩石的峰值应力影响最大,峰值应力随裂纹尺寸改变变化明显;预制裂纹角度对岩石峰值应力影响明显,但峰值应力的变化幅度相对于裂纹尺寸造成的变化较小。本次正交实验裂纹位置基本设置在距端部20mm以内,属于岩石内部裂纹,位置的改变对峰值应力无明显影响,峰值应力呈随机波动状态。经检验证明其是由实验组内产生的随机误差。方差分析不同几何特征对岩石峰值应力影响显著性的结果与上文单几何特征对岩石峰值应力影响结论一致。
4.2 裂纹几何特征对岩石力学性质影响程度量化分析
Partial Eta Squared(η2)为某影响因素对整体离差影响的效应值估量,其大小表示着主效应或互作效应的大小。
(7)
式中,SSX表示某一影响因素对实验结果造成的离差平方和;SSE表示实验误差造成的离差平方和。
因此根据其大小可以得出不同几何特征的改变对于岩石模型峰值强度的影响程度。从表5可得裂纹长度、倾角、位置对岩石力学性质影响程度大小分别为0.730,0.585,0.047。这表明对于岩石内部存在或产生的损伤,损伤的尺寸对于岩石的物理性质影响最大,现阶段对岩石损伤程度的描述多从损伤尺度出发;同等尺寸下损伤的角度对岩石物理学性质也有一定的影响,是由于角度影响了损伤尖端应力集中程度及损伤发育扩展的难易程度;对于岩石内部裂纹来说,裂纹的位置的改变对于岩石的物理性质影响微乎其微,相对于其他两种影响因素可以忽略。

表5 裂纹几何特征对岩石力学性质影响大小
5 结 论
为探究不同裂纹几何特征对岩石物理性质的影响程度,开展了包含裂纹尺寸、角度、位置3个影响因素的正交实验,并通过方差分析对其进行显著性检验,得到以下结论:
(1)岩石内部初始损伤中裂纹长度对岩石的力学性质影响最明显,裂纹的角度对岩石的力学性质影响次之,分布位置影响程度最小,其影响程度大小分别为0.730,0.585,0.047。
(2)裂纹长度影响了局部应力集中状态,进而影响到岩石的稳定性,随着裂纹长度增加岩石强度呈降低趋势。裂纹角度增大导致裂纹切向应力减小,降低裂纹尖端应力集中程度,加大裂纹发育的难度。岩石峰值应力随角度的增加呈上升趋势,且单位增加幅度逐渐加大。
(3)裂纹位置对于岩石峰值强度的影响在岩石端部区域与内部区域呈现较大差异:在端部区域,峰值强度随裂纹位置距端部的距离增加呈下降趋势;在内部区域预制裂纹位置对岩石峰值强度的影响不明显。

