基于波段选择与学习字典的高光谱图像异常探测

侯增福， 刘镕源， 闫柏琨， 谭琨

(1.中国矿业大学国土环境与灾害监测国家测绘地理信息局重点实验室，徐州 221116； 2.中国自然资源航空物探遥感中心，北京 100083)

0 引言

高光谱遥感影像不同于全色和多光谱遥感影像，具有光谱分辨率高、图谱合一的特点，在地物目标探测领域具有独特的优势，可广泛应用于环境监测和军事侦察等领域，然而在实际应用中研究者往往很难获得足够的先验知识来表征目标类别的统计信息，因此在没有可用先验信息辅助的情况下完成异常目标的探测，成为了近年来高光谱遥感影像目标探测领域的研究重点[1]。

在高光谱影像中，异常像元的光谱往往不同于周围背景像元的光谱信息，这就为异常像元能被探测出来创造了条件。由Reed和Yu在1990年发展起来的RXD(Reed-X detector)算法[2]，通过计算待探测像元与背景的马氏距离来完成异常探测，该算法选取整幅影像作为背景信息，故又称为全局RX(global RX，GRX)，由于使用全图均值和协方差来估计背景均值与协方差矩阵会影响探测精度，故对此改进的使用局部计算代替全局计算的RX又称之为局部RX(local RX，LRX)[3-5]。然而在真实高光谱影像中，背景信息复杂，使用估计的协方差与均值向量来表示背景信息并不准确。基于此提出的一些改进算法，如权重RXD(weighted-RXD，W-RXD)算法[6]和基于线性滤波的RXD(linear filter-based RXD，LF-RXD)算法[6]，这2种算法均旨在通过提高背景信息的估计来提高影像中异常被探测出的概率。一些基于核理论的探测算法，如较为经典的非线性核心RX探测(Kernel RX)算法[7]，相比于传统的探测算法[8]在异常探测中获得了较好的探测效果。

近年来，基于信号稀疏表示的算法也被应用于高光谱图像目标探测问题上[9]。然而这种算法仅仅考虑了影像的光谱信息，并没有顾及空间信息，故将其应用于异常探测中，往往难以取得令人满意的效果[1]。一种基于协同表示的异常探测算法[10](collaborative-representation-based detector，CRD)认为每一个背景像元都可以被其空间临域像元近似表示，而异常像元则不能，并在应用中取得了不错的探测效果。不同于信号稀疏表示的算法，赵锐等[11]通过在异常探测器的背景信息构建中引入鲁棒性分析方法，提出了一种在核特征空间中具有鲁棒性的异常探测算法； 张乐飞等[12]基于张量数据模型和张量代数运算，针对遥感数据多维或高维的特点提出了一种基于张量学习机的遥感影像目标探测算法； 彭波等[13]基于Cholesky分解，将高维矩阵的求逆运算转换为求解下三角线性系统，提出了基于Cholesky分解的逐像元实时高光谱异常探测算法。

目前，一些关于低秩分解的算法也被应用于高光谱异常探测中，如较为经典的鲁棒性主成分分析(robust principal component analysis，RPCA)算法[14]被应用于高光谱图像的异常探测中[15]，其中影像部分仅仅为单子空间表示，并没有考虑到高光谱影像中较为复杂的背景地物。针对该情况提出的低秩表示(low-rank representation，LRR)模型[16]，将低秩矩阵表示为多个子空间的线性组合。然而这种算法在使用时将自身作为字典，对应不同高光谱影像，最优参数往往不同，这是一个非常明显的缺陷。Xu等[9]首次将LRR模型引入到高光谱影像的异常探测中，提出了基于低秩和稀疏表示(low-rank and sparse representation，LRaSR)的异常探测算法。另一种基于低秩表示与学习字典(low-rank representation and learned dictionary，LRRaLD)的算法[17]在LRR模型的基础之上引入了仅包含背景光谱信息的学习字典，实现了高光谱背景与异常的有效分离，从而提高了算法的鲁棒性。

然而，由于高光谱本身数据的冗余性，使用上述算法进行异常探测时，往往需要较大的计算代价，如何在保留最大有用信息的同时，减少波段数量，从而达到减小计算代价的目的也就成为了研究的热点。基于此产生的数据降维算法可概括为2类： 特征提取[18-20]和波段选择。近些年来，波段选择算法广泛应用于遥感影像的分类研究中，并取得了不错的分类效果，如： 基于聚类分析的自组织特征映射神经网络(self-organizing feature map，SOM)[21-22]、流形学习应用于高光谱遥感影像[23]和最佳分形波段选择模型[24]。目前较为流行的蚁群优化算法也已经被应用于高光谱图像的降维中[25-28]。

在考虑到计算的复杂度和时间效率等综合因素后，本文引入了一种基于波段相似尺度的线性预测(linear prediction and band similarity metric，LPaBS)算法[29]，对原始影像进行预处理，即在原始波段特征空间进行选择，找到波段差异性最大的波段，从而形成原空间的一个子集，在最大程度上保留了波段的原始信息,同时降低了维度； 然后对选择的数据子集进行低秩表示与字典学习，并使用传统经典RXD算法进行异常探测，旨在减少计算代价的同时提高探测精度，较好地实现高光谱影像的异常探测。

1 算法研究

1.1 波段选择

高光谱遥感影像所具有的大量光谱波段为更加精细的地物分类与异常探测提供了极其丰富的信息，随着波段数的增多，其光谱特征组合方式更是以指数形式增长，导致了信息的冗余和数据处理复杂性的提高。分类器和探测器的性能在很大程度上依赖于数据降维的特征提取结果，依赖于这些特征是否能够精确地描述对象的特征[30]。本文所引入的LPaBS算法，通过在原始波段特征空间进行选择，找到波段差异性最大的波段，从而形成原空间的一个子集。

为了在高光谱影像中选出最具代表性的波段子集，需要某种尺度来衡量波段间的相似程度，常用方法有JM距离和空间相关性等，本文基于LPaBS算法选出差异性最大的波段A1和A2作为初始子集Ø，并通过Ø线性表示出其他波段，再继续通过基于LPaBS算法不断更新波段子集Ø，直到达到所要求的波段数。该方法中有2个初始参数，分别为初始波段对Ø和波段数。假设原始影像集共用N个波段，基于LPaBS法则[29]为： ①寻找初始波段对B1和B2，初始子集Ø={B1,B2}； ②根据评判标准选出波段B3，并通过Ø=Ø∪Bi升级子集Ø； ③继续步骤②，当子集Ø满足要求时停止。初始波段对的选择算法流程为： ①随机选出波段A1，并将其余N-1个波段投影到A1的正交子空间上，找出最大投影波段记为A2； ②将其他的N-1个波段投影到A2的正交子空间上，找到该投影空间上最大投影波段并记为A3； ③若A3=A1，则认为A1与A2是包含最多信息的波段对，停止循环，并将其作为初始波段对Ø，否则进入步骤④； ④对于波段Ai，继续步骤②和③，直到Ai-1=Ai+1，则将Ai-1与Ai作为初始波段对。关于评判波段相似性标准，假设当前波段子集Ø={B1,B2}，通过波段B1与B2线性预测波段B′，即

B′=a0+a1B1+a2B2，

(1)

a=(a0,a1,a2)T=(XTX)-1XTy，

(2)

式中：a为参数向量，可以最小化线性预测误差；X为一个N×3维矩阵，第1列元素全为1，第2列包含波段B1中所有像元，第3列包含波段B2中所有像元；y为一个包含波段B中所有像元的N×1维列向量； 波段B′为对波段B的线性预测值，通过最小二乘算法求解，即

(3)

式中E为预测波段误差。通过计算所有波段与B′之间的E，并找出最大误差对应的波段B3，B3即为所求波段。

1.2 低秩与学习字典

高光谱数据存在一个低维线性子空间，通过寻找该空间来实现对高光谱数据的降维处理，如经典的主成分分析(principal component analysis，PCA)算法，然而当高光谱数据中存在较大噪声或异常时，则不能取得理想效果[31]。有学者提出了RPCA[14]的算法，基于影像矩阵源于一个子空间的假设，将图像数据分解为低秩部分与稀疏部分[16]，即

Y=L+S，

(4)

式中：Y，L，S∈Rb×p，p为像元个数，b为波段数；L表示低秩矩阵；S表示稀疏矩阵。

不同于RPCA，假设LRR是基于高光谱数据矩阵由多个子空间构成，即

Y=DZ+S，

(5)

式中：D∈Rb×m表示字典，m为字典原子个数；Z∈

Rm×p为系数矩阵；S为包含异常值的稀疏矩阵。由于rank(DZ)≤rank(Z)故公式(5)的求解等价于

(6)

(7)

(8)

公式(8)的增广拉格朗日函数为[16-17]

(9)

在解决问题的过程中[16-17]，字典起到了很关键的作用，初始字典选取的好坏决定了字典收敛程度与收敛速度，在以往的研究中有些学者提出了使用数据本身作为字典的算法，在这种情况下平衡参数β起到了决定性的作用。若参数过小，探测率不高； 若参数过大，虚警率提高，针对这些问题有学者提出使用学习字典算法，这样在很好地解决平衡参数问题的同时提高了探测率，字典学习[17]的过程如下：

1)输入： 数据矩阵Y和字典原子个数m。

2)初始化：m=200，γ=0.01，μ=10，ε=10-6，D为归一化随机正值。

步骤1： 从高光谱影像中随机选择m个像元。

步骤2： 进行稀疏编码，其公式为

(10)

步骤3： 升级字典，其公式为

(11)

步骤4： 字典D归一化处理。

步骤5：μ→0.998μ。

3)输出： 学习字典D。

1.3 算法流程

提出的异常探测算法流程如图1所示，其主要过程为： ①使用线性预测法则对高光谱遥感影像进行波段选择，获得最终的高光谱波段子集； ②将高光谱波段子集转换为二维图像数据； ③利用字典学习过程进行字典学习，获得D； ④利用公式(9)将二维数据矩阵分解为L和E； ⑤利用RXD算法对E进行异常探测，获得最终探测结果。

图1 算法流程Fig.1 Framework of the proposed method

2 实验结果

为了对该算法进行验证，使用了4幅高光谱影像进行验证，其中1幅基于HyMap数据的模拟数据和3幅Hyperion，HYDICE，Hyspex真实高光谱遥感影像数据。

2.1 模拟数据

为了更好地验证本文算法效果，首先使用了1幅基于HyMap机载高光谱成像仪的模拟数据，该影像为2006年6月拍摄于美国马萨诸塞州区域，影像大小为280像元×800像元，如图2(a)。

(a) B14(R)，B8(G)，B1(B)真彩色合成影像

(b) 实验数据区域(c) 真实异常地物

图2HyMap数据集

Fig.2HyMapdataset

该影像含有126个波段，去除水汽吸收波段后余121个波段，实验中截取影像左侧中间大小150像元×150像元区域合成模拟数据，如图2(b)，选择红色棉布光谱作为异常光谱。基于线性混合模型，使用异常点埋入的方法生成模拟数据，其表达式为

z=ft+(1-f)b，

(12)

式中：z为合成异常数据；f为丰度分数；t为异常光谱；b为背景光谱。采用埋点的方法随机生成25个异常值，其中丰富分数为从0.05～1之间以等差数列形式生成25个丰度值。

为了评估本文提出的基于波段相似性尺度线性预测的低秩表示与学习字典(linear prediction and band similarity metric and low-rank representation and learned dictionary， LPaBS-LRRaLD)算法的优越性，分别与GRX，LRX，基于马氏距离的非监督最近邻规则子空间(unsupervised nearest regularized subspace with Mahalanobis distance，UNRS-MD)[32]与LRRaLD等算法进行对比分析。

首先通过基于HyMap数据合成的模拟数据来证明提出算法的可行性，模拟数据为121个波段，通过LPaBS 算法选出具有代表性的80个波段。各种算法异常探测结果及对应的接收者操作特性曲线(receiver operating characteristic，ROC)如图3所示，表1列出了每种算法的ROC曲线下面积(area under ROC curve，AUC)与运行时间2个定量评价指标。

(a) GRX(b) LRX(c) UNRS-MD

(d) LRRaLD(e) LPaBS-LRRaLD(f) ROC曲线

图3HyMap模拟数据探测结果及ROC曲线
Fig.3DetectionresultsandROCcurvesofHyMapsimulationdataset

表1 HyMap模拟数据AUC与耗时性比较Tab.1 Comparison of AUC and execution time using HyMap simulation data

由图3与表1可以看出，使用LRRaLD和LPaBS-LRRaLD算法能够获得较好的探测效果，但是LPaBS-LRRaLD算法在探测精度与运行时间上都优于LRRaLD算法。

2.2 真实数据

2.2.1 HYDICE 数据

Urban数据是由HYDICE机载高光谱成像仪于城市上空拍摄而得到的空间分辨率近1 m的高光谱遥感影像，整幅影像大小为307像元×307像元，包含210个波段，去除低信噪比与水汽吸收波段后剩余174个波段，截取整幅影像右上角80像元×100像元的子块与其对应的真实异常地物如图4所示。

(a) B49(R),B36(G),B18(B)真彩色合成影像(b) 实验数据区域(c) 真实异常地物

图4HYDICE数据集

Fig.4HYDICEdataset

为了利用HYDICE高光谱成像仪获取的Urban数据证明本文提出算法的可行性，首先使用 LPaBS 算法选出具有代表性的100个波段，再采用LRRaLD算法进行异常探测。各种不同算法的异常探测结果及其对应的ROC曲线如图5所示，表2列出了各种算法的AUC和运行时间。

(a) GRX(b) LRX(c) UNRS-MD

(d) LRRaLD(e) LPaBS-LRRaLD(f) ROC曲线

图5HYDICE数据集探测结果及ROC曲线
Fig.5DetectionresultsandROCcurvesofHYDICEdataset

表2 HYDICE数据集AUC与耗时性比较Tab.2 Comparison of AUC and execution time using HYDICE data set

通过图5可以看出，在各种算法中，使用LRRaLD和LPaBS-LRRaLD算法能够获得较好的探测效果。由表2数据可知，GRX算法运行时间最短，但是探测精度明显低于LRRaLD和LPaBS-LRRaLD算法，LPaBS-LRRaLD算法在探测精度与运行时间上明显优于其他算法。

2.2.2 Hyperion 数据

Hyperion遥感影像数据含有242个波段，光谱分辨率为10 nm ，波长范围为357～2 576 nm。实验使用的影像数据采集于2008年，影像中主要包括美国印第安纳州的农业区。去除低信噪比与未定标波段后余149个波段，在实验中使用含有真实异常数据的150像元×150像元大小的子区域(如图6所示)完成实验，影像中异常值主要为储物仓库和屋顶。同样，为了验证本文算法的有效性，首先基于LPaBS 算法选出具有代表性的100个波段，然后使用学习字典并利用增广拉格朗日公式求解进行异常探测，各种不同算法的探测结果及其对应的ROC曲线如图7所示，每种算法的AUC与运行时间如表3所示。

(a) B29(R)，B23(G)，B16(B)假彩色合成影像(b) 真实异常地物

图6Hyperion数据集

Fig.6Hyperiondataset

(a) GRX(b) LRX(c) UNRS-MD

(d) LRRaLD(e) LPaBS-LRRaLD(f) ROC曲线

图7Hyperion数据集探测结果及ROC曲线
Fig.7DetectionresultsandROCcurvesofHyperiondataset

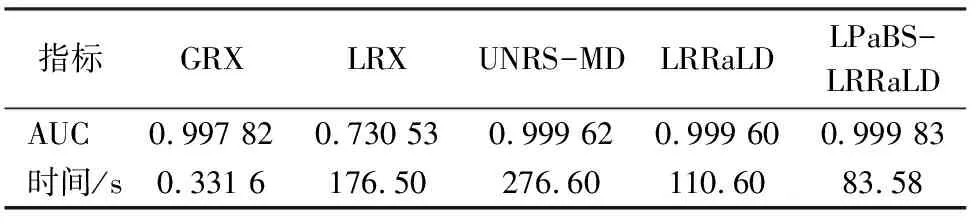
表3 Hyperion数据集AUC与耗时性比较Tab.3 Comparison of AUC and execution time using Hyperion data set

通过图7可以看出，使用Hyperion数据进行异常探测，除LRX算法外，其他探测算法均具有较高的探测精度，其中LPaBS-LRRaLD算法探测精度最高。由表3数据可知，GRX算法运行时间最短，但是探测精度均低于UNRS-MD，LRRaLD和LPaBS-LRRaLD算法，其中LPaBS-LRRaLD算法在探测精度与运行时间上明显优于其他算法。

2.2.3 Hyspex 数据

该数据是由机载Hyspex高光谱成像仪于2014年11月在徐州泉山区附近拍摄的条带影像，包含160个可见光波段与288个短波红外波段，光谱范围为415 ～2 508 nm，空间分辨率近1 m，实验中截取条带中340像元×260像元区域，其中异常值为彩钢房屋，影像与真实异常地物如图8所示。

(a) B63(R)，B38(G)，B13(B)真彩色合成影像(b) 真实异常地物

图8Hyspex数据集

Fig.8Hyspexdataset

在Hyspex数据集中，首先基于LPaBS 算法选出具有代表性的45个波段，然后使用学习字典算法进行异常探测。

各种探测算法实验结果及各种算法的ROC曲线如图9所示，每种算法的AUC与运行时间如表4所示。

(a) GRX(b) LRX(c) UNRS-MD

(d) LRRaLD(e) LPaBS-LRRaLD(f) ROC曲线

图9Hyspex数据集探测结果及ROC曲线
Fig.9DetectionresultsandROCcurvesofHyspexdataset

表4 Hyspex数据集AUC与耗时性比较Tab.4 Comparison of AUC and execution time using Hyspex data set

通过图9可以看出，使用Hyspex数据进行异常探测，其中的 LPaBS-LRRaLD算法探测精度明显高于其他算法。由表4数据可知，除GRX算法运行时间最短外，LPaBS-LRRaLD算法在探测精度与运行时间上明显优于其他算法。

2.3 实验小结

通过模拟数据与真实数据实验，可以看出本文提出算法的可行性，对照实验中所使用的RXD算法与最近提出的UNRS-MD和LRRaLD算法都是基于原始数据进行的异常探测，而本文提出算法在降维的同时探测精度得到了提高，尤其是Hyspex数据，波段数从448个减少到45个，很大程度上去除了信息冗余，在减少计算代价的同时探测精度也得到了提高。

3 结论

针对全局高光谱异常，将低秩分解的算法引入到高光谱异常探测中，并通过低秩分解将图像表征为背景低秩矩阵与稀疏矩阵，在求解背景低秩矩阵过程中采用学习字典来提高背景字典的准确性与鲁棒性，同时顾及维数灾难对高光谱影响异常探测的影响。首先，采用基于波段相似性线性预测的算法进行降维，在保持原有波段信息不变性的同时有效地去除数据冗余； 然后，结合学习字典算法在低秩分解过程中提高背景与异常信息可分性的同时，更好地挖掘数据本身的低秩特性，从而达到快速收敛； 最后，使用传统的RXD算法对稀疏矩阵进行异常探测。

实验表明，本文算法与同类算法相比，在高光谱影像异常探测中，在进一步降低计算代价的同时，提高了异常探测率，因此该算法更具有实际应用意义。由于学习字典的随机性，会使得背景字典中存在异常的小概率事件发生，针对这种情况，如何找到完全不存在异常的背景字典来表征背景矩阵，从而使得背景与异常更加有效地分离将是需要进一步研究的问题； 同时也建议尝试其他探测算法对稀疏矩阵进行异常探测，以达到更高精度的探测率。