递归滤波与KNN的高光谱遥感图像分类方法

涂兵， 张晓飞， 张国云， 王锦萍， 周瑶

(1.湖南理工学院信息与通信工程学院，岳阳 414006； 2.湖南理工学院复杂系统优化与控制湖南省普通高等学校重点实验室，岳阳 414006； 3.湖南理工学院IIP创新实验室，岳阳 414006)

1 引言

高光谱遥感图像因其具有较高的光谱分辨率和丰富的光谱信息[1]，被广泛应用于精确农业、环境监测和公共安全等方面[2]。作为高光谱应用系统中的关键技术，快速高精度的高光谱图像分类算法是实现各种实际应用的前提[3]。近年来，高光谱图像分类成为了国内外的研究热点。在早期研究中，许多经典的模式识别与机器学习算法，如最大似然分类法[4]和支持向量机(support vector machine，SVM)分类算法[5]，被有效应用于高光谱遥感图像分类中。但是,这些算法仅利用高光谱图像的光谱信息，忽略了其空间结构信息的作用，因而无法有效提高分类精度。

随着研究人员的深入挖掘，发现通过将光谱信息和空间信息有效融合，可大大改善高光谱遥感图像的分类结果。由于局部空间区域内有较大的概率属于同一类别，且其光谱值也可能非常相近。因此，一种基于分割的高光谱图像分类方法[6-10]被提出，这类方法通过提取像元间相邻的空间信息实现图像分割，且可取得较好的分类效果，但大部分算法时间复杂度较高。为解决这一问题，李旭超等[11]提出了马尔可夫随机场方法，该方法通过将像素空间关系紧密地结合在一起，可用低阶的马尔可夫随机场描述像素间的作用关系，减少方法时间复杂度。由于该方法对纹理结构要求高，分割效果也需进一步改进。在此基础上，Tarabalka等[12]提出了一种基于markers的最小传播森林分割分类方法(minimum spanning forest，MSF)，充分考虑邻近像素的空间与光谱信息，通过选取粗分类中可信度最高的像素点为标记点(markers)作为MSF的初始点，实现对像素点区域的平滑与精准分割，取得了较好的实验效果。

同时基于特征提取的空间与光谱分类[13-16]方法也被提出。Camps-Valls等[17]提出了一种基于数学形态学特征合成核的SVM分类算法，此算法利用空间统计特征作为空间信息，通过不同的合成核构造方式，有效地将空间信息和光谱信息融合应用于高光谱图像分类； Zhang等[18]通过将光谱、纹理和形状特征结合，构成特征向量，进而使用SVM算法实现最终分类； Kang等[19]提出了边缘保持滤波的特征提取算法，通过利用双边滤波与引导滤波有效保持高光谱遥感图像的边缘特性，从而提高分类精度。

以上结合空间与光谱信息的分类方法虽然取得了较好的效果，但性能上仍有进一步提升的空间。为此，本文提出一种融合递归滤波(recursive filtering，RF)与KNN(k-nearest neighbor)的高光谱遥感图像分类方法，利用RF算法有效去除高光谱图像中的噪声，强化空间结构，充分利用地物目标的空间上下文信息，然后利用KNN算法计算图像像素点的欧式距离，进行决策分类。

2 方法原理

2.1 RF算法

RF算法的原理为对给定的变换域Ct： Ω→Ωω和输入图像I，可通过域变换将输入图像I转换到变换域Ωω中。首先利用图像的空间结构信息，计算输入图像I的每个像素转换前的坐标Ct(xm)，再计算每个像素变换后的坐标Ct(xs)，计算结果表明位于同侧图像边缘像素具有相似的坐标，而位于异侧图像边缘像素坐标相距较远，基于此原理，可在转换域中定义RF，即

J[m]=(1-ab)I[m]+abJ[m-1] ，

(1)

(2)

式中：I′(x)为I(x)的导数；δr表示范围标准差。将图像I进行域变换处理，当式(1)中ab趋近于0，式(2)中的递归过程逐渐收敛，使得滤波后输出结果中同一侧图像边缘的像素会取得相近的值，不同侧图像边缘的像素会有很大差别，从而有效保留图像中的边缘信息。

2.2 KNN算法

NN(nearest neighbor)分类器的原理是通过距离度量为测试样本找到最邻近的训练样本，根据训练样本类别来决策测试样本的类别。KNN算法基于此原理，已知训练样本标签的类别，寻找测试样本的k个最相似或最邻近的训练样本，然后根据k个最邻近的训练样本类别来决策测试样本的类别。计算测试样本与训练样本之间的欧式距离为

(3)

式中：xi为训练样本集中第i类样本；yi为测试样本的第i类样本；n为空间维数。

2.3 RF-KNN分类方法

本文提出的RF-KNN分类方法实现过程主要为4步骤： ①利用主成分分析法(principal component analysis，PCA)对高光谱图像进行降维； ②对降维后的PCA分量图像进行RF，强化空间结构信息； ③计算测试样本与每一类训练样本的欧式距离； ④选取与测试样本距离最近的k个测试样本，根据k个训练样本的类别判断测试样本所属类别。

2.4 评价指标

在完成高光谱图像分类后，需要对高光谱图像的分类结果进行客观评价。通常依据地面参考数据，评估分类结果的准确性。采用4个常见的高光谱图像分类精度指标来衡量分类算法的精度： 每类分类精度(class accuracy，CA)、整体分类精度(overall accuracy，OA)、平均分类精度(average accuracy，AA)以及Kappa系数。同时，为了避免实验存在随机误差，每个实验重复20次记录平均结果与方差。

3 实验数据及参数分析

3.1 实验数据集

采用Indian Pines和 Salinas这2个高光谱数据集作为实验数据集，分别如图1和图2所示。2景遥感图像均来自AVIRIS(airborne visible infra-red imaging spectrometer)光谱仪收集到的高光谱遥感图像，Indian Pines影像为1992年在印第安纳州西北部地区影像，具有20 m的空间分辨率，由于噪声和水吸收等因素除去其中的20个波段，剩余200个波段，图像范围大小为145像素×145像素，其中包含16种地物。Salinas影像为美国加利福尼亚州萨利纳斯山谷地区影像，含224个波段，空间分辨率为3.7 m，图像范围大小为512像素×217像素，其中包含16种地物，由于噪声和水吸收等因素亦除去遥感图像中的20个波段。

(a) B40波段影像(b) 地面参考数据(c) 颜色编码

图1IndianPines区域实验数据

Fig.1IndianPinesdataset

(a) B100波段影像(b) 地面参考数据(c) 颜色编码

图2Salinas区域实验数据

Fig.2Salinasdataset

3.2 实验参数分析

为了得到最佳的分类精度，对RF算法中的δs和δr、最近邻数k以及维度Dim进行分析。分别在Indian Pines和Salinas数据集上进行试验，获取最优分类结果对应的参数值。

通过确定RF算法中δs和δr的值，使滤波效果达到最佳。首先确定RF算法中这2个参数的取值范围，如图3所示。

(a) Indian Pines数据集(b) Salinas数据集

图3RF参数对不同数据集分类精度的影响分析

Fig.3AnalysisofRFparametersonclassificationaccuracyindifferentdatasets

在分析δr影响时，δs为固定值，随着δr值增大，平均分类精度明显降低。这是因为δr值较大时，RF会退化为高斯滤波，造成影像过度模糊而丢失有用的形状和轮廓等空间结构信息，导致物体的分类错误。而当δs和δr取最小值时，就意味着在特征提取过程中仅考虑较小邻域的局部空间信息，而忽略整体空间信息，则会导致滤波效果较差。由图3可知，在Indian Pines数据集上，当δs=212且δr=0.9时，能得到最优分类精度； 在Salinas数据集上，当δs=210且δr=0.7时，获得最优分类精度。

分析最邻近数k对分类精度的影响时，仅改变k参数，其余参数选为常数。如图4所示，当k=1时，2个数据集都能获得最高的分类精度，分别为98.96%和99.51%。随着k的增加，引入的噪声数据也会相应增加，导致分类精度下降。

(a) Indian Pines数据集(b) Salinas数据集

图4最近邻数k对不同数据集分类精度的影响分析

Fig.4Analysisofthenumberofnearestneighboronclassificationaccuracyindifferentdatasets

此外，特征维度Dim也是影响高光谱分类精度的重要因素。实验分析如图5所示。

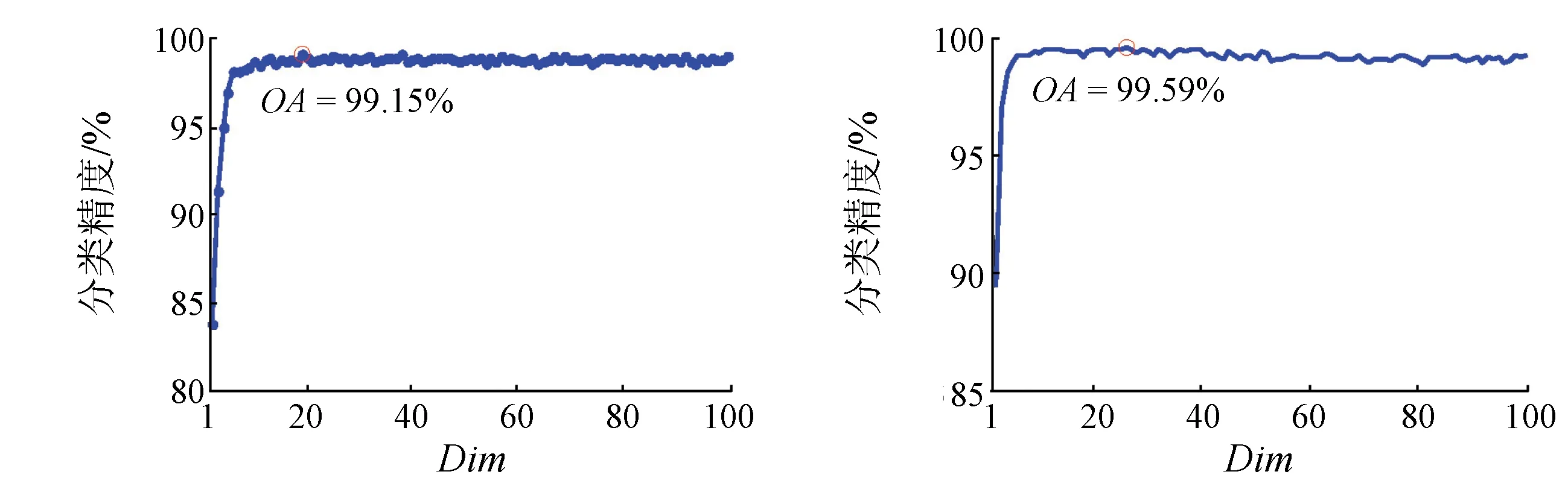
(a) Indian Pines数据集(b) Salinas数据集

图5维度对不同数据集分类精度的影响分析

Fig.5Analysisofdimensiononclassificationaccuracyindifferentdatasets

当Dim=4时，分类精度较低。其原因是图像降维过程中会丢失大量有用的光谱信息，使分类精度降低。随着Dim增加，2个数据集的分类精度变化趋势类似，都是先增加再保持不变。在Indian Pines数据集上，当Dim=20时，分类精度最高； 在Salinas数据集上，当Dim=30时，分类精度最高。

4 实验结果与分析

4.1 不同分类算法比较

为了验证本文提出方法的优越性，实验比较了本文提出的方法与传统的分类算法和几种空谱分类算法的分类效果，其算法包括： 传统分类算法SVM[5]、稀疏表示分类(sparse representation classification，SRC)[20]算法、联合稀疏表示分类算法(joint sparse representation classification，JSRC)[21]、扩展形态特征(extended morphological profiles，EMP)算法[22]、边缘保持滤波(edge preserving filtering，EPF)的算法[23]、基于图像融合和递归滤波(image fusion and recursive filtering，IFRF)的算法[19]以及逻辑回归与多层回归(logistic regression and multi-level logistic，LMLL)算法[24]。在进行实验比较之前，先设置不同类算法的参数。SVM的最佳参数通过10次交叉验证确定。对于EMP算法，利用HSI的前3个主成分分量，形态学算子的尺寸依次递增2个像素，共进行4次形态学开闭和重构运算，构建多尺度形态学特征。对于EPF算法，使用前4个主要部件，圆形结构元件、二阶梯形增量及4个开口和关闭构造形态轮廓进行参数设置。对于SRC，JSRC，IFRF和LMLL算法，实验均采用默认参数，通过Matlab编写代码实现。

4.2 实验结果

4.2.1 Indian Pines数据集

在Indian Pines数据集中，随机选取10%作为训练样本，剩余的90%作为测试样本。为了分析训练样本数量对算法分类精度的影响，再采用1%的训练样本和99%测试样本进行实验。不同算法分类结果如图6和图7所示。

(a) SVM(b) SRC(c) JSRC(d) EMP

(e) EPF(f) IFRF(g) LMLL(h) RF-KNN

图6不同算法在IndianPines数据集的分类结果(10%训练样本)

Fig.6ClassificationresultsofdifferentalgorithmsintheIndianPinesdataset(10%oftrainingsamples)

(a) SVM(b) SRC(c) JSRC(d) EMP

(e) EPF(f) IFRF(g) LMLL(h) RF-KNN

图7不同算法在IndianPines数据集的分类结果(1%训练样本)

Fig.7ClassificationresultsofdifferentalgorithmsintheIndianPinesdataset(1%oftrainingsamples)

对于仅使用光谱信息的SVM分类算法而言，分类结果中噪声点较多，并且每种地物类型与实际地物类型对应关系错误率也较高，分类精度较低。相比SVM分类算法，EMP算法在分类时通过利用图像空间结构信息总是能获得更高的分类精度，然而在分类结果中一些“噪声”状的误分类仍然可见。相比EMP算法，EPF算法通过边缘保持滤波联合空间信息与光谱分类结果，能提升分类精度。对于本文提出的RF-KNN方法而言，不但利用RF算法平滑了噪声，增强空间结构，而且还结合空间邻域信息进行分类，分类精度优于其他空谱分类算法。当训练样本极少时，本文提出的方法依然能获得较好的分类精度。比如能准确地识别位于实验区右上方的地物类别。该方法通过有效地联合空间信息，对大多数地物类别的识别精度均优于其他空谱分类算法。

表1和表2分别显示了训练样本数、测试样本数和不同分类算法的分类精度。表中括号外数值表示各个精度均值，单位为%，括号内数值表示各精度的均方差，下同。

表1 Indian Pines高光谱图像不同算法分类精度(10%训练样本)Tab.1 Indian Pines data set classification accuracy of different algorithms (10% of training samples)

表2 Indian Pines高光谱图像不同算法分类精度(1%训练样本)Tab.2 Indian Pines data set classification accuracy of different algorithms (1% of training samples)

由表1和表2可知，本文提出的RF-KNN方法在OA，AA和Kappa指标上有相对的优势。SRC的分类算法精度最低，SVM算法在训练样本占地面参考数据10%的情况下，能够有效地区分Wheat，Woods和Stone等光谱区分度较大的地物，然而由于未考虑高光谱图像的空间信息，对于一些光谱类似的地物，分类识别精度不高。例如，Oats的分类精度仅为46.35%。相比SVM算法，其他空谱分类算法能提升分类精度，但对某些类别的分类精度较低，比如对于Soybean的识别。本文的RF-KNN方法能取得最高的分类精度。例如Grass-P，Hay-W和Oats的分类精度能达到100%，大多数类别上的分类精度均高于98%； 相比SRC算法，对于Alfalfa的识别，提高了32.86%。在训练样本占地面参考数据1%的情况下，大部分算法识别精度明显下降，而本文方法依然能获得最佳的分类精度，且对Grass-P和Hay-W的分类精度仍保持为100%。

4.2.2 Salinas数据集

在Salinas数据集中，将所有数据分为训练样本和测试样本。随机选取参考数据中的2%作为训练样本，其余作为测试样本。并进一步改变训练样本的数量进行实验，随机选取参考数据中的0.2%作为训练样本，剩下99.8%的参考数据作为测试样本。Salinas数据集不同算法分类结果如图8和图9所示，SVM算法分类结果中噪声点较多。与仅使用光谱信息的SVM算法相比，JSRC算法通过联合空间信息能有效去除这种类似噪声的误分类，提高了分类精度。相比其他7种高光谱遥感图像分类算法，本文所提出的RF-KNN方法总能获得更高的分类精度，其原因在于利用RF算法有效地平滑了噪声，强化了地物轮廓，对图像区域边缘划分效果较好。随着训练样本数量的减少，JSRC，EPF和LMLL算法分类结果中出现明显误分类现象，IFRF算法和RF-KNN方法均能在训练样本减少时较好地区分各种地物覆盖类别。虽然两者均有去除图像噪声与增强影像空间结构的特性，但是相比于IFRF算法，RF-KNN方法通过加入空间近邻信息进一步提高了分类精度。分类精度分别如表3和表4所示。

(a) SVM(b) SRC(c) JSRC(d) EMP

(e) EPF(f) IFRF(g) LMLL(h) RF-KNN

图8不同算法在Salinas数据集的分类结果(2%训练样本)

Fig.8ClassificationresultsofdifferentalgorithmsintheSalinasdataset(2%oftrainingsamples)

(a) SVM(b) SRC(c) JSRC(d) EMP

图9-1不同算法在Salinas数据集的分类结果(0.2%训练样本)

Fig.9-1ClassificationresultsofdifferentalgorithmsintheSalinasdataset(0.2%oftrainingsamples)

(e) EPF(f) IFRF(g) LMLL(h) RF-KNN

图9-2不同算法在Salinas数据集的分类结果(0.2%训练样本)
Fig.9-2ClassificationresultsofdifferentalgorithmsintheSalinasdataset(0.2%oftrainingsamples)

表3 Salinas高光谱图像不同算法分类精度(2%训练样本)Tab.3 Salinas data set classification accuracy of different algorithms (2% of training samples)

表4 Salinas高光谱图像不同算法分类精度(0.2%训练样本)Tab.4 Salinas data set classification accuracy of different algorithms (0.2% of training samples)

从表3和表4可以看出，本文提出的RF-KNN分类方法均能获得最高的分类精度。相比SRC算法，对于一些识别分类不准确的类别，比如Graps，从73.62%提高到了99.87%，Vinyard_U的识别精度提升了37.60%，在Soil类别中识别精度可以达到100%。相比其他的空谱分类算法，大部分类别分类精度都高于97%； 当训练样本极少时，本文提出的方法识别精度均优于其他的空谱分类算法； 对于Soil的分类精度仍保持100%。SRC，JSRC，EMP和EPF算法的分类精度明显下降。实验证明，RF-KNN方法能有效联合高光谱图像的空间信息与光谱信息，进而提升地物覆盖类别的识别精度。

5 结论

在本文所提出的基于递归滤波和KNN的高光谱图像分类方法较好地结合光谱和空间邻域信息，有效降低了错误分类概率。该方法通过在2个经典实验数据库上进行实验并且与其他算法进行了对比验证，结果表明，与现有高光谱遥感图像分类算法相比，该方法在不同训练样本下都具有较好的分类性能，并且具有较好的鲁棒性，为高光谱遥感图像分类领域提供了新的研究思路与方法。但在实验过程中，该方法的时间复杂度较高，因此如何有效降低该方法的时间复杂度是下一步研究的重点。

志谢： 康旭东博士提供了EPF和IFRF算法代码，李军教授提供了LMLL算法代码，在此一并表示感谢。最后，感谢李树涛教授和康旭东博士对论文给出的深刻意见。