基于边缘采样的简化高阶CKF在非线性快速传递对准中的应用

卢航，郝顺义，彭志颖，黄国荣

空军工程大学 航空工程学院， 西安 710038

传递对准是目前一种常用的动基座对准方法[1-2]。在舰载环境下，利用舰船高精度的主惯导系统对舰载机低精度的子惯导系统进行传递对准可以有效提高对准精度和缩短对准时间[3-5]。传递对准分为粗对准和精对准两个过程[1]，粗对准过程中，主惯导对子惯导提供姿态、速度、位置等导航信息完成一次装订，随后子惯导以此装订值为基础开始姿态解算和导航解算。建立传递对准误差模型并采用卡尔曼滤波器进行估计的过程为精对准过程，在实际主、子惯导系统传递对准工作过程中，杆臂效应误差、舰船夹板挠曲运动误差是两个较为主要的误差因素。为了提高传递对准工作精度，通常在滤波器观测量中对杆臂效应带来的速度误差进行补偿，以减弱其所带来的影响。舰船实际航行过程中，在日晒、阵风、海浪冲击等外界因素的作用下，其船体结构通常会产生一定的变化，杆臂的长度会因为挠曲运动的存在也会发生变化，此时存在动态杆臂[6-14]。文献[6-8,15]建立了载舰挠曲变形和杆臂效应的一体化传递对准误差模型，但是均对3个失准角进行了小角度假设，实际上，舰载机可能停靠在舰船甲板上的任意位置，而舰船主惯导系统却安装在甲板下方的导航室，此时主、子惯导系统之间的方位失准角可能很大，那么基于小角度假设的传递对准一体化误差模型已经不适用于这种情况，需要对大失准角情况下的非线性传递对准一体化误差模型进行进一步研究。文献[9]提出了适用于大方位失准角的非线性传递对准模型，但是该模型并没有对实际失准角进行建模，同时量测方程是复杂的非线性方程，这无疑会造成滤波算法精度和数值稳定性的下降。文献[10]通过对姿态量测量进行安装误差角的补偿，提出一种适用于安装误差角为大失准角情况下的姿态匹配方法，但是该方案需要提前知道安装误差角，具有一定的局限性。需要指出的是，文献[6-10]所提出的传递对准模型均是建立在计算导航坐标系内，Kain和Cloutier于1989年提出了基于量测失准角的传递对准误差模型，并引入计算载体系，建立了一种新的“速度加姿态匹配”快速传递对准误差模型[11]。文献[12-14,16]在此基础上建立了非线性快速传递对准模型，但是并没有进一步考虑挠曲变形和杆臂效应二者带来的综合影响。

本文针对舰载机惯导系统非线性传递对准误差模型不完善的问题，同时考虑载舰挠曲变形和杆臂效应两种主要误差因素，建立挠曲变形和杆臂效应加速度一体化误差模型。采用“速度+姿态”组合匹配算法，设计了一种适用于该模型的基于边缘条样的简化高阶容积科尔曼滤波(M-RHCKF)算法，最后进行仿真实验，结果证明了所建立模型的正确性和滤波算法的有效性。

1 非线性快速传递对准一体化模型

1.1 坐标系定义

模型的推导过程主要涉及到以下几种坐标系，以各坐标系的x轴为例，它们之间的关系如图1所示。

导航坐标系n取当地地理坐标系；舰船坐标系m的坐标原点位于舰船中心位置，它与标称机体坐标系s0之间的失准角定义为实际失准角φa；标称机体坐标系s0与实际机体坐标系s之间相差挠曲变形角θ；舰船坐标系m与计算机体坐标系s′之间的失准角定义为量测失准角φm。

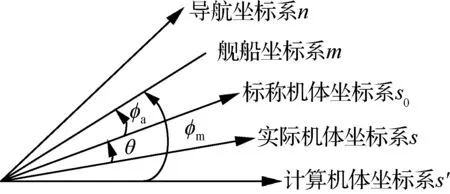
图1 各坐标系关系图Fig.1 Diagram of each coordinate system

1.2 挠曲变形和动态杆臂一体化建模

目前大多数研究认为Markov过程可以较好地描述挠曲变形运动[6-9,15,17]，此时甲板的挠曲变形角可以看做是由一个白噪声激励的二阶Markov过程，可以表示为

(1)

(2)

(3)

(4)

(5)

图2 θz引起的动态杆臂示意图Fig.2 Diagram of dynamic lever arm caused by θz

(6)

(7)

同理可以得到由于y轴方向上的挠曲变形在x、z轴上的影响，z轴方向上的挠曲变形在x、y轴上的影响，表1为θ在另两个轴向上引起的杆臂误差。

表1挠曲变形角在y轴和z轴上引起的杆臂误差

Table1Lever-armerroronyaxisandzaxiscausedbyflexuraldeformationangle

挠曲变形角误差y轴z轴θxy01-sinθxcosθxθx()y0sin2θxθxθyz01-sinθycosθyθy()θzx0sin2θzθz

在动态杆臂δr影响下的杆臂长度为

(8)

当挠曲变形角满足小角度假设时，θ′满足sinθ′≈θ′，cosθ′≈1，那么式(8)可以简化为

(9)

动态杆臂δr可以表示为

δr=L0θ

(10)

对式(10)左右两边求1阶导、2阶导可得

(11)

(12)

式(12)结合式(1)后可以进一步表示为

(13)

式中：

(14)

(15)

由图3可知，舰船在航行时会产生船体摇摆，通常认为主惯性组件的安装位置为船体的摇摆中心，由于子惯性组件的安装位置和舰船摇摆中心的位置不一致，导致子惯导的加速度计中包含干扰加速度，从而主、子惯导导航计算机解算的速度信息不同的现象称为杆臂效应误差，主、子惯性组件敏感到的比力信息之间的差异称为杆臂加速度误差。

图3 杆臂效应示意图Fig.3 Schematic diagram of lever-arm effect

Oixiyizi坐标为惯性坐标系，Omxmymzm为主惯导载体坐标系，Osxsyszs为子惯导载体坐标系，根据图3中矢量关系可得

(16)

(17)

(18)

(19)

(20)

(21)

1.3 主、子惯导姿态误差模型

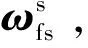
(22)

(23)

考虑到挠曲变形角可以近似为小角度，式(23)可以改写为

(24)

由姿态矩阵微分方程容易得到[11-14,16]

(25)

(26)

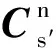
(27)

式(27)两边同时求微分得到

(28)

(29)

(30)

将式(30)代入式(29)得到

(31)

由反对称矩阵的性质可以得到

(32)

将式(24)代入式(32)得到

(33)

(34)

式中：

(35)

将式(33)代入式(34)，得到非线性传递对准姿态误差方程为

(36)

1.4 主、子惯导速度误差模型

主惯导的速度微分方程为

(37)

基于计算载体坐标系的速度微分方程为

(38)

(39)

通常情况下，固定杆臂引起的杆臂速度误差可以在速度误差量测量中进行补偿，但是无法补偿动态杆臂加速度引起的速度误差量，将式(21)代入式(39)即可得到非线性一体化速度误差方程为

(40)

式中:

2 基于M-RHCKF算法设计

2.1 传递对准的状态方程与观测方程

将式(10)两边同时微分可以得到动态杆臂δr的微分方程为

(41)

(42)

(43)

由式(1)、式(36)、式(40)～式(43)可以构成非线性一体化传递对准状态方程。

采用“速度加姿态”匹配模式，速度观测量可以通过求取主、子惯导速度差值并对标称杆臂r0进行杆臂速度补偿后得到。姿态观测量可以由主、子惯导的姿态阵相乘得到，其表达式为

(44)

不难发现量测失准角φm即做状态变量也做观测量，此时的量测方程为简单的线性方程，观测矩阵H为

(45)

2.2 简化高阶CKF(RHCKF)算法

HCKF算法的滤波精度可以达到5阶[18-19]，相比于传统的CKF或UKF算法的3阶估计精度具有明显优势，但是其每次在时间、量测更新过程中的容积变换需要采样(2n2+1)个容积点，所以，较大的计算量也是限制其应用的一个原因。为了保留滤波算法的高精度优势，由式(45)可知，本文提出的快速传递对准模型中的量测方程为线性，故可采用简化量测更新过程(具体证明过程见附录A)代替传统的HCKF量测更新过程，只需在时间更新过程中进行一次容积变化即可完成全部滤波算法，具体算法流程如下。

1) 滤波器初始化

(46)

2) 时间更新过程

① 计算容积点Xi,k-1|k-1(i=0,1,…,2n2)。

奇异值分解(SVD)相比于传统的Cholesky分解可以更好地解决协方差矩阵病态条件的问题，该分解方法没有要求协方差矩阵满足对称性和正定性的条件，使得整个算法具有更高的数值稳定性和滤波精度，对协方差矩阵Pk-1/k-1使用SVD分解，即

(47)

(48)

式中：S=diag(s1,s2,s3,…,sr)，s1≥s2≥s3≥…≥sr≥0，U∈Rm×m，V∈Rn×n，为矩阵Pk-1/k-1的奇异值;ξi为求积分点集，当采用5阶容积准则时，共有2n2+1个求积分点，其具体表达式为[7-9]

(49)

(50)

(51)

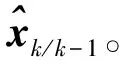
(52)

式中：ωi为容积点的权值，如式(53)所示

ωi=

(53)

④ 计算k时刻的预测误差协方差阵Pk/k-1。

(54)

3) 简化量测更新过程

⑤ 计算更新后的状态容积点Xi,k|k-1。

(55)

式中:Pk/k-1=Sk|k-1(Sk|k-1)T。

⑥ 计算经过量测方程传递的容积点Zi,k|k-1。

Zi,k|k-1=HkXi,k|k-1

(56)

(57)

⑧ 计算k时刻的量测误差协方差阵Pzz,k|k-1和预测互相关协方差阵Pxz,k|k-1。

(58)

(59)

4) 滤波更新过程

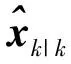
Kk=Pxz,k|k-1(Pzz,k|k-1)-1

(60)

(61)

Pk|k=Pk|k-1-KkPzz,k|k-1(Kk)T

(62)

显然，RHCKF算法只需在时间更新过程中进行一次容积变换，量测更新过程则不需要。所以相比于传统HCKF算法，基于SVD分解的SHCKF具有更少的计算量和更强的数值稳定性。

2.3 非线性快速传递对准模型的部分线性结构

采用欧几里德方法对状态方程进行离散化处理[20-21]，离散间隔为dt，离散形式的非线性快速传递对准模型可以写为

(63)

式中：

A=

B=

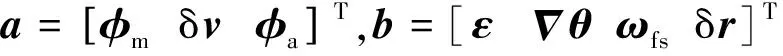
γ(a(k))·b(k)

(64)

式中:ψ(a(k))和γ(a(k))分别表示为

(65)

(66)

2.4 基于边缘采样的高阶CKF(M-HCKF)算法

(67)

式中:ψ(·)为非线性函数;γ(·)为非线性函数或线性函数。假设状态变量x服从高斯分布，它的均值与方差可以表示为

(68)

(69)

可以得到高斯随机变量b相对于高斯随机变量a的条件均值E(b|a)和条件协方差Pb|a的表达式为[20-22]

(70)

(71)

此时随机变量y的均值和方差可以表示为

E(y)=∬(ψ(a)+γ(a)b)p(a,b)d(ab)=

(72)

Py=∬(y-E(y))(y-E(y))T·p(a,b)d(ab)=

∬(ψ(a)+γ(a)b-E(y))·(ψ(a)+

γ(a)b-E(y))T·p(a,b)d(ab)=

γ(a)Pb|aγ(a)T]·p(a)da

(73)

式中:φ(a)=ψ(a)+γ(a)·E(b|a)。想要求得式(72)、式(73)的解析解是比较困难的，可以采用高斯近似求和滤波的思想得到它们的数值积分解，结合2.2节提出的HCKF算法，选择高阶容积采样规则计算均值和方差，此时E(y)和Py可以表示为

(74)

γ(ξi)Pb|aγ(ξi)T]

(75)

3 仿真实验

设置载体的初始位置为东经127°，北纬30°，高度0 m，载体初始速度大小为10 m/s，方向正北，舰船做匀速直线运动，仿真总时长为120 s。SINS的解算周期为0.01 s，舰载机子惯导的陀螺和加速度计的参数如表2所示，假设舰船主惯导系统无误差。

假设舰船在海浪的作用下做如下形式的3轴摇摆运动：

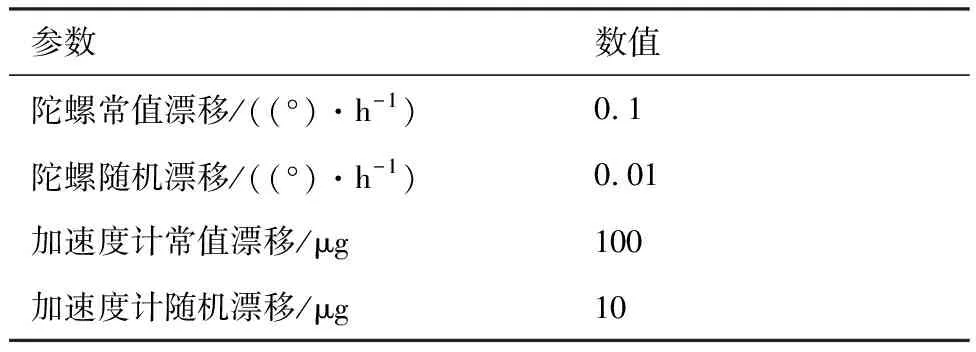
表2 惯性测量组件主要性能参数Table 2 Parameters of inertial measurement module

式中：θm、γm和φm为舰船的摇摆幅度(θm=12°，γm=15°，φm=10°);ωi=2π/Ti(i=θ,γ,φ)为摇摆频率(Tθ=8 s，Tγ=10 s，Tφ=6 s);αi(i=θ,γ,φ)为初始相位角(αθ=0°,αγ=0°,αφ=30°);标称杆臂长度r0=[10 m10 m20 m]T，实际失准角φa=[0.5°0.6°10°]T，2阶Markov相关时间τi=60 s(i=x,y,z)。

图4和图5分别为M-RHCKF和RHCKF对姿态失准角φ和实际失准角φa的估计曲线。可以看到，姿态失准角大约在10 s后收敛到稳态，实际失准角φa大约在20 s后收敛到稳态。这是因为对于采用“速度+姿态”匹配的快速传递对准模型而言，由于观测量中含有量测失准角的的信息，所以即使舰船不做加速机动，M-RHCKF和RHCKF均可以对姿态失准角φ和φa进行有效的估计。表3为M-RHCKF和RHCKF在100 s至120 s时间段的姿态失准角φ和实际失准角φa的估计误差统计表。由表3可知M-RHCKF算法在具有更少采样点的情况下滤波精度与RHCKF相当，两者的估计结果验证了边缘采样算法的有效性。

图4 M-RHCKF和RHCKF对失准角的滤波估计Fig.4 Filter estimation of misalignment angle using M-RHCKF and RHCKF

图6为挠曲变形角θ的估计曲线，图7为动态杆臂δr的估计曲线。从图6和图7可以看出大约在20 s后RHCKF和M-RHCKF两者趋于稳定，均可以跟踪上挠曲变形角和动态杆臂的变化。由标称杆臂长度r0并结合式(10)可知，由于r0在z轴的分量最大，产生沿x轴上的动态杆臂误差同样最大，同理沿y轴上的动态杆臂误差最小，这与图7中δr的真实值曲线是相符合的。

表4为未考虑动态杆臂的传递对准模型和提出的一体化传递对准模型在滤波收敛后最后40 s的均值和方差统计表。显然，对于未考虑动态杆臂的传递对准模型而言，由于速度误差模型中没有包含动态杆臂速度误差项，此时速度误差模型与实际情况是失配的，然而一体化传递对准模型在子惯导比力中考虑了动态杆臂加速度误差项，建立了动态杆臂δr的数学模型，与舰船航行中的实际情况更相符，所以相比于前者具有更好的滤波性能。

图5 M-RHCKF和RHCKF对实际失准角的滤波估计Fig.5 Filter estimation of true misalignment angle using M-RHCKF and RHCKF

表3两种滤波算法的估计误差统计(100～120s)

Table3Estimatederrorstatisticsoftwofilteralgorithms(100-120s)

估计误差M-RHCKFRHCKFϕx/(′)1.36721.3792ϕy/(′)1.70811.7998ϕz/(′)1.33911.3169ϕax/(′)0.58310.5384ϕay/(′)0.87520.8329ϕaz/(′)1.19681.1213

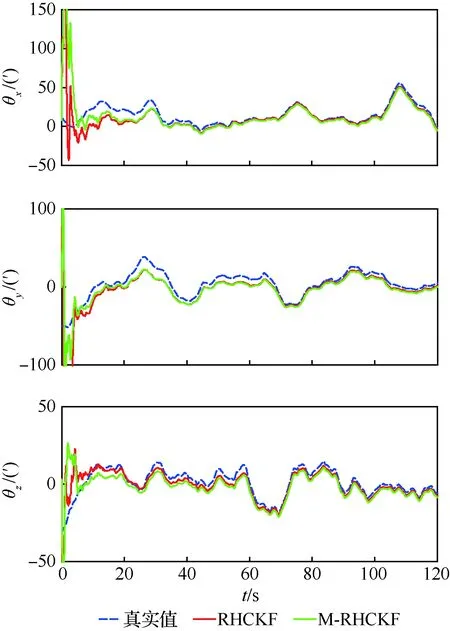
图6 M-RHCKF和RHCKF对挠曲变形角的滤波估计Fig.6 Filter estimation of flexural deformation angle using M-RHCKF and RHCKF

图7 M-RHCKF和RHCKF对动态杆臂变形的滤波估计Fig.7 Filter estimation of dynamic lever arm deformation using M-RHCKF and RHCKF

为了比较M-RHCKF和RHCKF算法的运行时间，仿真软件采用MATLAB2014A，仿真处理器为Intel inside core i5处理器，分别对M-RHCKF和RHCKF两种算法进行50次仿真实验，得到两种滤波算法的总运行时间和平均单次运行时间如表5所示。

由表5可知M-RHCKF算法所消耗的运行时间较RHCKF算法更少，结合表3的计算结果，结果证明边缘采样算法和简化量测更新过程可以在保持滤波精度的同时可有效减小计算量，具有更强的实用性。

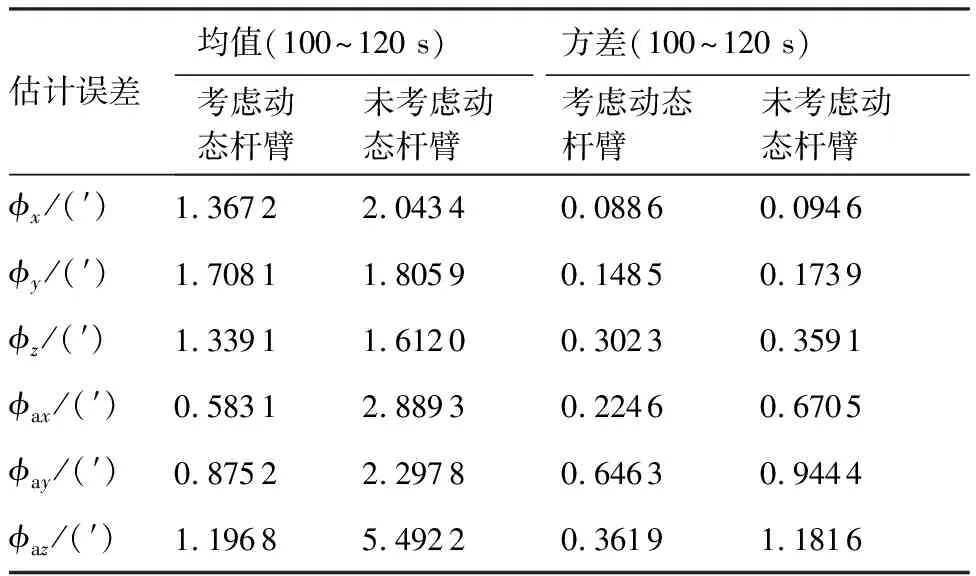
表4 两种模型估计误差统计Table 4 Estimated error statistics of two models

表5 两种滤波算法运行时间统计Table 5 Statistics of running time for two filtering algorithms

4 结 论

1) 建立了一种非线性一体化快速传递对准模型，并验证了其正确性，该模型不对实际失准角和姿态失准角进行小角度假设，可以准确估计出挠曲变形角和动态杆臂，具有更广阔的应用范围。

2) 分析了所提出的快速传递对准误差模型的部分线性结构，结合该特点设计了一种基于边缘采样的M-RHCKF算法。理论分析证明该算法相比于传统的HCKF具有更小的计算量，可以满足传递对准精度和时间的要求。

3) 实际中由于各种外界因素的影响，在无法准确获得挠曲变形和动态杆臂变化特性的条件下，可以通过研究鲁棒非线性滤波算法达到抑制挠曲变形和动态杆臂影响的目的。