基于超短基线声传感器阵的高速目标轨迹估计
陈昭男,孙翱,王磊,阎肖鹏
1. 中国人民解放军 91550部队,大连 116023 2. 大连海事大学 航海学院,大连 116023
低空飞行目标是常规雷达探测技术的盲点,近年来对该类目标的被动声学探测方法逐渐成为研究热点[1-2]。低空高速飞行目标威胁性更高,且更加难以跟踪,目前对该类目标的被动声学探测相关研究还相对较少。以声速为界限,高速低空飞行目标可分为超声速目标和低于但接近于声速目标两大类,前者飞行噪声呈现明显的激波特征,因此可通过检测激波脉冲前沿并结合波达方向估计方法来实现[3-4];对于后者将其称为高亚声速飞行目标。高亚声速飞行目标噪声是一类瞬态信号,难以准确获取其信号特征,给其定位跟踪带来了较大困难。
目前对低空飞行目标的研究主要集中在直升机、无人机等低速目标,相关的定位和跟踪方法研究主要在时域、频域和空间谱域内进行,其对应的跟踪方法也可分为基于时延估计的目标定位方法[5-8],基于瞬时频率的目标运动参数估计方法[9-15]和基于空间谱估计的测向方法三大类[16-22]。近年来代表性的研究成果主要有:Kam等[5]提出了一种基于声多径传播模型的目标运动参数估计方法,该方法利用不同路径声信号的到达时间估计值,实现对目标运动参数的估计,该方法要求布设尽可能多的长度基线声传感器阵;佟建飞等[9]对瞬时频率方法进行了拓展,提出了一种基于单声传感器阵列的目标运动轨迹估计方法,首先利用多普勒效应估计目标飞行参数,结合波达方向估计目标轨迹方向、水平偏置和高度,依据几何模型确定其运动轨迹,该方法主要适用于低速飞行目标;陈华伟[16]提出了基于五元十字阵的低空目标声测无源定位算法,在时延估计方面,提出了基于维纳加权的频域自适应时延估计算法和基于双谱的时延估计算法,在小尺寸高精度定向方面,首次将压差式矢量声传感器引入低空目标侧向研究中,提出基于矢量传感器阵的宽带相干信号子空间最优波束形成算法,子空间类方法的角估计精度高,但计算量较大,同时还需要部分先验信息进行引导。
论文以利用布设于有限空间内的声传感器阵实现低空高速目标跟踪为背景,通过对某典型低空高速目标噪声波形的分析,发现其噪声呈现宽带低频谱特征,因此主要研究了基于时延估计的目标定位跟踪方法,提出了多面交汇的目标轨迹估计方法,并推导了其估计误差的理论表达式。
1 信号特征分析
掌握低空高速飞行目标的噪声特性是对其进行定位和跟踪的前提。某低空飞行目标的飞行速度最高约为294 m/s(马赫数Ma约为0.86),这里选用该类目标作为典型高亚声速低空飞行目标。利用拾音器对该类目标在实际飞行全过程中的噪声进行了采集。该目标空中飞行轨迹约为200 m,其轨迹末端以土堆作为靶标,拾音器置于其飞行轨迹正下方靠近靶标的位置。这里对测得的实际噪声进行了频谱分析,结果如图1所示。

图1 某典型目标飞行噪声频谱Fig.1 Flight noise spectrum of typical target
由图1可见,所采集的目标飞行噪声频谱呈现宽带低频特性,这是由于高频噪声在空气中传输时功率衰减较快,仅有低频部分能够被拾音器有效接收。同时,该噪声频谱也没有明显的离散点频率。因此,对于该类目标的声学跟踪问题,难以通过多普勒频移方法对其运动参数进行估计,可考虑采用多路时延法或空间谱估计方法。空间谱估计方法往往计算量较大,而该类噪声信号的低频分量一般信噪比较大,适于采用多路时延方法。基于以上分析,这里基于高速低空飞行目标的时域噪声波形,研究利用多路时延的目标定位和跟踪方法。
2 定位跟踪模型
实际应用中,由于布设条件的制约,长基线声基阵的应用经常受到限制,本文主要研究利用布设于有限空间内的声传感器阵列对目标进行估计的方法。超短基线声基阵所需要的安装空间较小,布设灵活,因此这里对基于超短基线声传感器阵的高速运动目标跟踪方法展开研究。
这里采用均匀线性空间十字阵阵列模型,同时以超短基线阵建立直角坐标系。基准传感器为坐标原点,声传感器均匀分布于x轴、y轴和z轴的正负半轴上,6个边缘传感器与基准传感的距离,即基线长度均为L。超短基线传感器阵由5k+1 (k≥1,k为正整数)个声传感器组成。超短基线阵布设位置如图2所示。

图2 超短基线阵布设示意图Fig.2 Distribution diagram of ultra-short baseline arrays
假设超短基线阵位于声源远场,此时声波为平面波。假设目标入射波的方位角和俯仰角分别为φ和θ,则入射波的单位方向向量k表示为
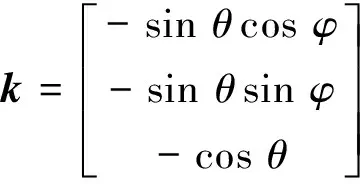
(1)
该向量在某一坐标轴上相邻两个声传感器连线矢量上的投影,即为该方向声信号的传播路径差。基准传感器位于坐标原点,则任意传感器相对基准的传播路径差为k在该传感器坐标向量上的投影,因此第i个位于[xi,yi,zi]的传感器Ai相对于基准传感器O的时差τi的表达式为
τi=αik/c=-(xisinθcosφ+
yisinθsinφ+zicosθ)/c
(2)

(3)
(4)
同时,根据式(1)和式(3),利用所测量得到的目标入射波在3个坐标正半轴上的传感器时延量,可直接估计得到目标入射波单位方向向量的估计值,即
(5)
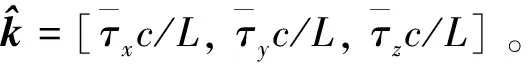

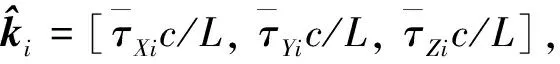
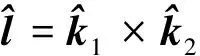
(6)
目标运动方向向量归一化估计值为
(7)
(8)
利用多个平面方程相交,可以得到目标运动轨迹上某一点的坐标,从而完成对目标运动轨迹的估计。当超短基线阵的数目N=3时,3个平面相交即可得到轨迹点的坐标。当N>3时,利用最小二乘法估计得到轨迹点的坐标,此时轨迹点方程可以写成
(9)
该式可写成矩阵的形式
Ax=b
(10)
轨迹点坐标的最小二乘估计值为
x=[x0,y0,z0]=(ATA)-1ATb
(11)

(12)
3 测向及定位误差分析
(13)

根据测量误差传播原理,目标轨迹俯仰角估计的均方根误差σθ可以表示为
(14)
根据文献[16],在各个声传感器时延估计误差相同的情况下,入射波估计方位角的均方误差表达式为
(15)
根据式(4),推导得到入射波俯仰角估计均方根误差表达式为
(16)
根据式(14)~式(16),同时忽略较小项,可得目标轨迹的俯仰角估计均方根误差约为
(17)
上述表达式中变量较多,将其整合成sinφ12、sinθ1和sinθ2等3个变量的形式:
(18)
假设所有时延估计量的均方根误差στ是相同的,对于方位角,由于其表达形式比较复杂,这里直接对各个时延量求偏微分,得到其均方根误差表达式为

(19)

下面对导致角度误差发散的因素进行分析。σθ和σφ共同决定了目标运动方向角度估计误差的大小。根据式(18)和式(19),可能导致角度估计误差发散的共同变量为其分母中的|sin(k1,k2)|,当两个声传感器阵到目标运动方向垂线矢量,即入射波方向矢量k1,k2相互平行时,其角度估计误差将趋向于无穷大。对于超短基线阵,至少需要两组互不平行的入射波方向矢量k,才能实现对目标运动轨迹的估计。只有当各个基阵中心与目标运动轨迹均在同一个平面上时,其对应的所有k均平行,此时将无法对目标角度进行估计。因此,为能够实现对目标运动轨迹的估计,各个超短基线阵应尽量保证与目标运动轨迹不在同一平面上。为进一步提高角度估计精度,两个超短基线阵的入射波方向k应尽量垂直,此时|sin(k1,k2)|接近于1。对于方位角估计的均方根误差σφ,能导致其误差发散的变量还有方位角φ本身,当方位角φ接近90°,即与y轴平行时,将无法实现对目标方位角的估计。
下面对位置估计的理论误差进行推导。假设超短基线阵1和2位于一个统一坐标系中,其中心点坐标分别是[x1,y1,z1]和[x2,y2,z2],两个超短基线阵均位于同一平面上,其各自超短基线阵的z轴正向相对于统一坐标系的方位角分别为φ01和φ02。当超短基线阵的数目N=3时,根据式(7)和式(8),可得对目标轨迹点[x,y,z]的估计方程可以写成
(20)
式中:aij(i=1,2,3,j=1,2,3)为中间变量,ai1=l2τzi-l3τyi,ai2=l3τxi-l1τzi,ai3=l1τyi-l2τxi。将式(20)可看作是时延向量τ=[τx1,τy1,τz1,τx2,τy2,τz2,τx3,τy3,τz3]的隐函数,目标轨迹点坐标[x,y,z]为函数,aij为中间变量。对式(20) 中时延向量求全微分,可得
(21)
式中:ai=[ai1,ai2,ai3]T,xi=[x-xi,y-yi,z-zi]T,J1、J2、J3、Jx均为ai和[x,y,z]的Jacobi矩阵转秩,
其他Jacobi矩阵的形式与之类似。Jx为目标位置坐标[x,y,z]关于时延向量的Jacobi矩阵形式,是需要求解的未知量,可通过求解方程组式(21) 得到,几何精度因子(Geometric Dilution Pricision,GDOP)的值根据Jx表达式进一步推导得到。
4 仿真结果及分析
4.1 时延估计误差对目标测向精度影响
对典型布站情况下一定测向误差所要求的时延估计精度进行了仿真分析。假设阵列长度L=0.5 m,采用4个超短基线阵,阵元中心坐标分别为[0,10,1],[24,0,3],[-25,0,5],[0,-9,7],目标轨迹方向的xOy平面分量为[1,1],俯仰角分别取45°、60°、85°和90°,经过xOz平面上的轨迹点为[1,0,1],在σθ和σφ均满足0.1°≤σ≤5°时,所要求的时延估计精度如图3所示。这里俯仰角为目标运动方向相对于z轴正向的角度。
由图3可见,在俯仰角为90°,即目标水平飞行时,角度估计对时延误差的要求最低,当时延估计误差在ms级,方位角和俯仰角的估计误差均可保证在1°以内。对于方位角估计而言,目标越接近于水平运动时,对时延估计精度要求越高,在俯仰角为85°时,0.1°方位角估计均方根误差要求时延估计误差στ≤7.4 μs,1°对应的时延估计误差στ<74.2 μs。对于俯仰角估计,其估计误差与目标运动俯仰角不呈现直接比例关系。在图3(a)给出的4种情况中,俯仰角为60°时,俯仰角估计对时延估计精度的要求最高,0.1°俯仰角估计均方根误差要求时延估计误差στ≤3.19 μs,1°对应的时延估计误差στ<31.9 μs。综合两类角度的仿真结果来看,要达到0.1°的角度估计均方根误差,时延估计精度应该在μs级,而想要达到1°的角度估计均方根误差,时延估计精度应达到30 μs。
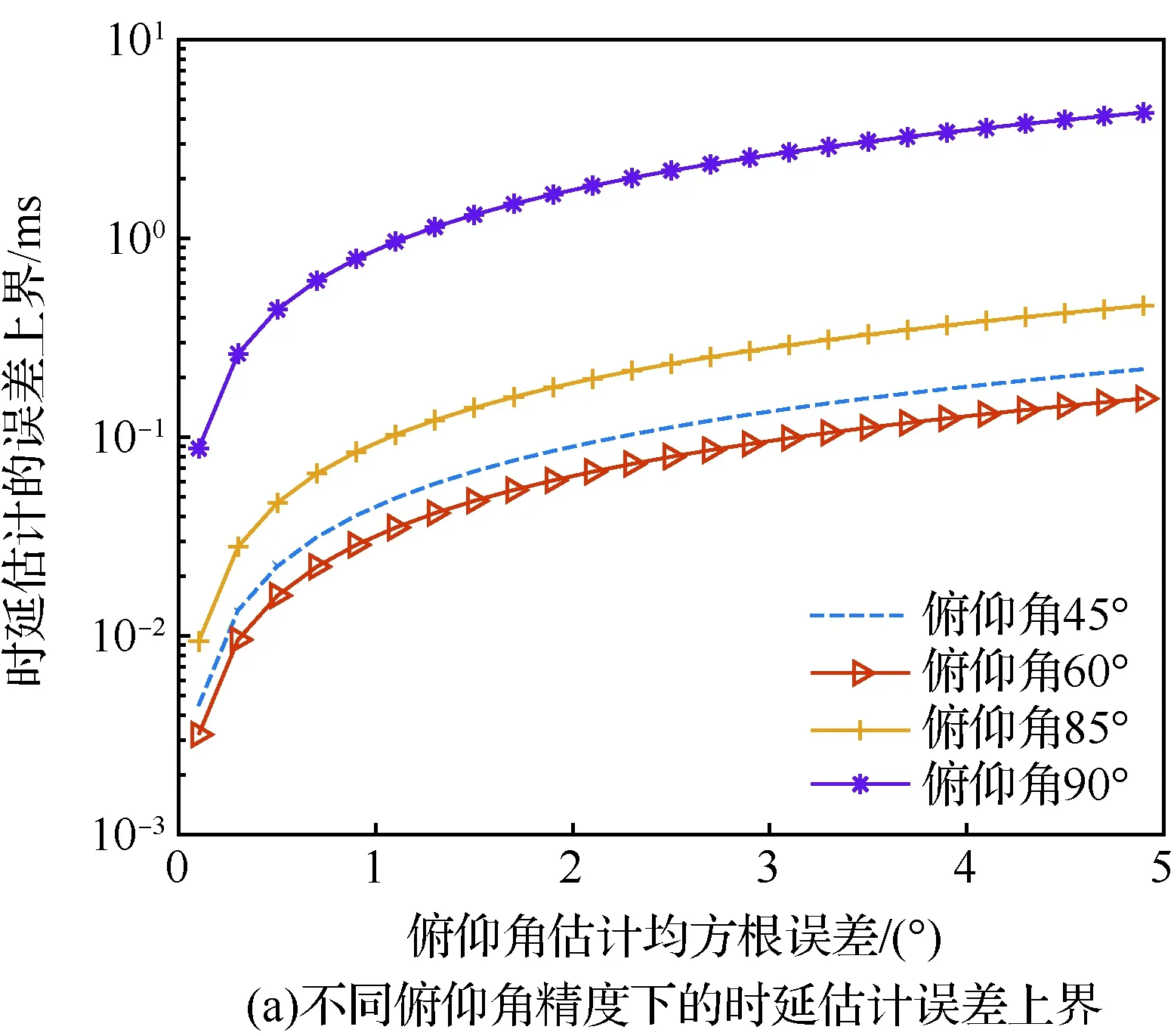
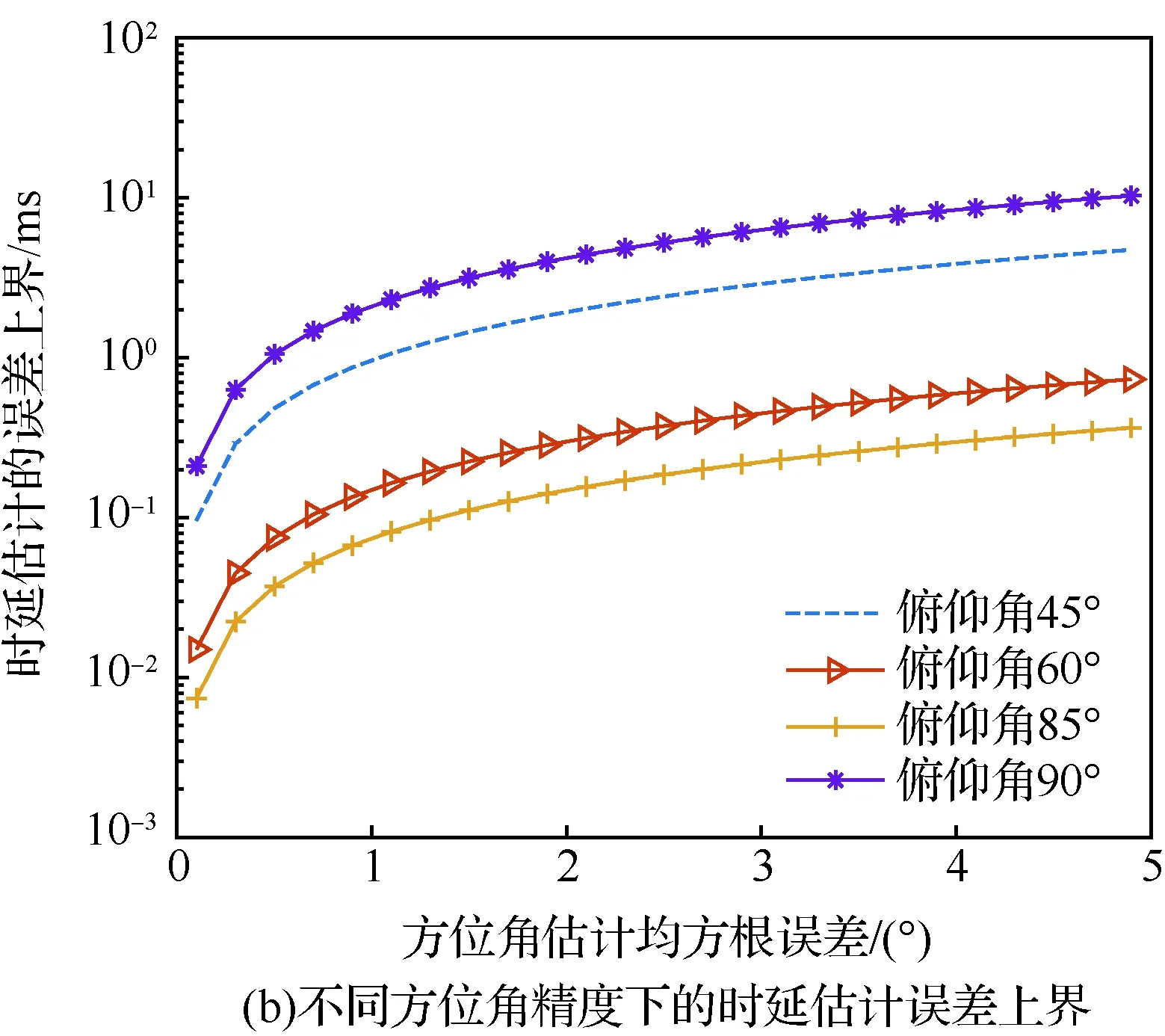
图3 不同角度精度下的时延估计误差上界Fig.3 Time delay estimation error upper bounds at different angle accuracies
4.2 不同布站方式下目标测向及定位误差仿真

观察图4发现,2种入射方向下,其角度误差基本分布在2°以下。根据误差计算结果,这一入射方向情况下对目标入射角估计的平均误差为2.01°,验证了该方法用于目标角度估计的有效性。角度误差的区域极值点分布在传感器基阵附近,但并没有明显规律。根据角度误差理论公式式(17)和式(19),在45°俯仰角情况下的理论角度误差应更大,但由于其传感器基阵数目较多,明显提高了其角度跟踪精度。在图4(b)中,其估计误差极值区域分布更加分散,这是由于传感器阵数目较多,将极值区域“分割”了。
根据图5,轨迹点位置坐标的相对估计误差基本在5%以内。根据计算结果,这两种入射方向情况下对目标位置估计的平均相对误差为4.87% 和5.08%,验证了本方法用于位置估计的有效性。图5中的相对误差结果总体较为相近,其均值和峰值也近似相同,这也说明多个超短基线阵补偿了俯仰角对误差的影响。与图5(a)相比,图5(b)的区别主要在于位置误差极值分布区域更加集中了,主要集中在3个椭圆形区域。由于位置估计需要通过多个平面交汇一点得到,出现3个极值区域说明该区域内的多个平面接近平行,难以获得较为准确的估计结果。


图4 角度估计误差在xOz面上的分布Fig.4 Distribution of angle estimation error on xOz plane

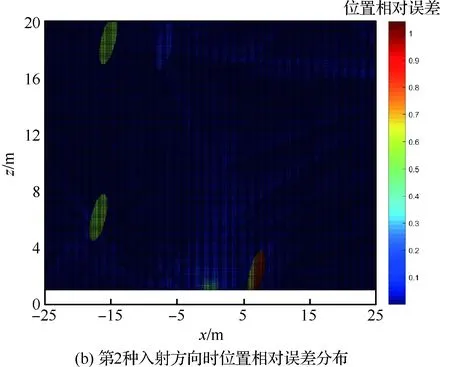
图5 位置相对误差在xOz面上的分布Fig.5 Distribution of relative location error on xOz Plane
在不同超短基线阵数目L和轨迹方向的情况下,角度和位置估计的平均误差仿真结果如表1所示。由表1可知,在相同入射角的情况下,采用更多的超短基线阵可以获得更高的角度估计精度,根据表中给出的3种入射方向相同的情形,采用10基阵情况下的角度估计精度大约是4基阵情形下的2倍;而对于位置估计,10基阵在目标水平运动状态下的估计精度反而不如4基阵的情形,在45°俯仰角时,10基阵的位置估计精度要优于4基阵,但优势并不明显。随着目标俯仰角的增加,角度估计精度提高,这也验证了角度误差理论公式的结果。在方位角方面,随着方位角的增加,角度估计精度变差,在45°时估计精度最低,随后精度逐渐恢复,在目标垂直x轴入射时,理论上可实现无误差估计。位置估计精度与方位角和俯仰角(此处特指目标飞行轨迹与水平面的夹角)也呈现负相关,在方位角90°时,位置估计精度最高,随后逐渐变低,当目标平行x轴飞行时,位置估计精度最低;随着俯仰角的增加,目标位置估计精度也逐渐降低。
表1不同基阵数目和轨迹方向时角度和位置估计的平均误差
Table1Averageerrorofangleandpositionestimationfordifferentarraynumbersandtrajectoryorientations

基阵数目目标轨迹方向向量轨迹方向平均误差/(°)xOz平面轨迹点相对误差/%10[1, 1, 0]1.2510[1, 5, 0]0.494.8310[1, 1, 2]2.055.084[1, 1, 0]2.014.874[1, 5, 0]0.784.254[0, 1, 0]03.84[1, 1, 2/2]3.245.184[1, 1, 2]3.846.554[1, 1, 0.5]2.965.044[5, 1, 0]0.919.97
对于利用有限空间内的多个声超短基线阵实现目标跟踪的问题,根据上述仿真结果,可得到以下结论:
1) 随着目标俯仰角增加,角度估计精度提高。
2) 超短基线阵数目增加,可有效提高角度估计精度,也可减少估计奇异值点。
3) 在目标垂直于xOz平面入射时,其角度估计精度最高。
根据仿真结果可知,在传感器布设于有限空间内时,该方法可实现对目标运动轨迹的有效跟踪,并能实现较好的效果,在采用4个传感器基阵时,角度估计平均误差在4°以内,位置估计相对误差在5%左右。
5 结 论
1) 本文方法的优势在于:① 利用有限空间内的声传感器阵列,通过几何交汇的方式,实现了对高亚声速飞行目标的估计;目前被动声学跟踪方法仅适用于低速飞行目标,本方法扩展了被动声学方法所跟踪目标的范围;② 实现了在复杂电磁环境下对低空飞行目标的有效跟踪,同时也能够对低空高速隐身目标进行感知和探测。
2) 由于声传感器布设空间的制约,该方法在进行目标角度和方位估计时,仍存在一定的估计奇异值点,如何减少和消除奇异值点是后续需要研究的内容。

